First we define the Green's function for the ODE:

> G:=(x,y)->piecewise(y>=0 and y <=x,y*(1-x),x<=y and y<=1,x*(1-y));

and then the solution of the ODE using the Green's function is given by:

> x:='x':f:='f':sol:=int(G(x,y)*f(y),y=0..1);

Limit the range of x:

> assume(x>0);additionally(x<1);

Define ODE for the dsolve:

> ode:=-diff(v(x),x$2)=f(x);

First case:

> f:=y->y*y;

> u:=eval(sol);

Let's try to use dsolve to see if it gives the same solution:

> sol2:=dsolve({ode,v(0)=0,v(1)=0},v(x));

OK. Solutions are the same. Let's verify the solution by differentiating and evaluating u(0) and u(1):

> -diff(u,x$2);

> subs(x=0,u);

> subs(x=1,u);

Finally here is a plot of the solution:

> plot(u,x=0..1);

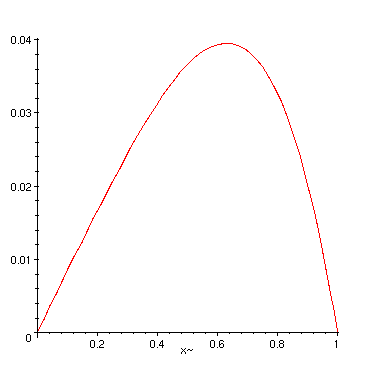
Second case:u(0);

> f:=y->exp(y);

Maple does not show the argument of exp, is it a bug? Anyway the internal representation seems to be correct. Solution with Green's function:

> u:=eval(sol);

Solution with dsolve:

> sol2:=dsolve({ode,v(0)=0,v(1)=0},v(x));

Verification:

> -diff(u,x$2);

> simplify(subs(x=0,u));

> subs(x=1,u);

Plot of the solution:

> plot(u,x=0..1);

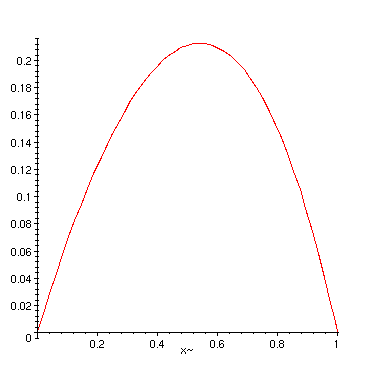
Third case:

> f:=y->cos(a*y);

> u:=eval(sol);

Solution with dsolve:

> sol2:=dsolve({ode,v(0)=0,v(1)=0},v(x));

Verification:

> -diff(u,x$2);

> simplify(subs(x=0,u));

> subs(x=1,u);

Plot of the solution:

> plot(subs(a=1,u),x=0..1);

>
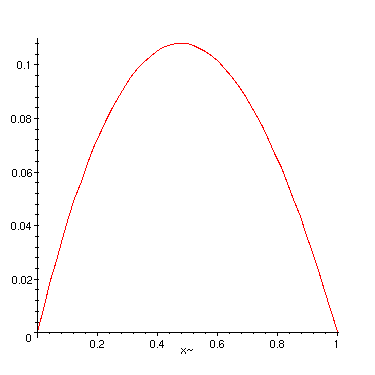