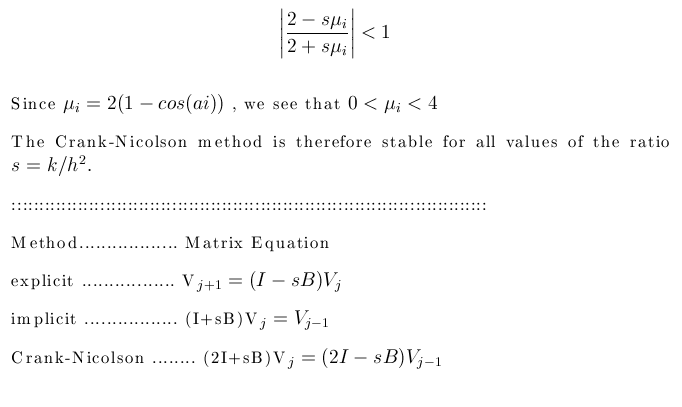Numerical Solution Of Partial Differential Equations

Parabolic Equations

<Durbo@math.hut.fi> Mat-1.174 Computational PDE
Course Teacher H.Apiola

Explicit Methods
Implicit Methods
Crank-Nicolson Method
Algorithms and Examples
Stability Analysis which includs the following two methods:

Matrix Method
Fourier Method

References

Introduction to Numerical Analysis by E. Atkinson.
Numerical Analysis 5th edition by Burden and Faires
Course Material

We will consider one of the well-known partial differential equation (PDE):

HEAT EQUATION

The heat equation can be written in 3-D as :
u_xx+u_yy+u_zz=u_t where u=u(x,y,z,t).
To simplify the procedure we will take one dimensional heat equation:
u_xx=u_t , t>0, 0<x<1 ........(1)
u(x,0)=g(x) , 0<x<1
u(0,t)=a(t),
u(1,t)=b(t)

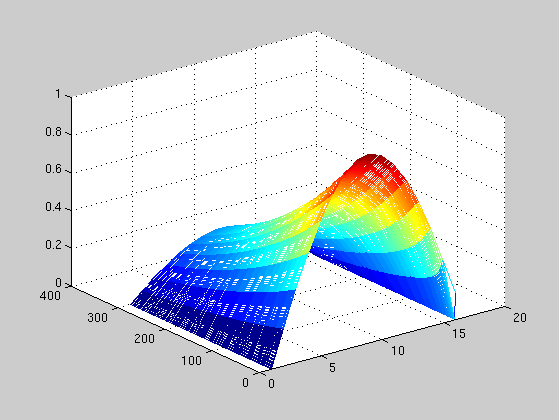
Equation (1)describes the temperature distribution in a rod of length one with temperatures a(t),b(t) at its ends and initial temperature g(x).

Explicit Methods

To solve equation (1) numerically we will use Finite Difference Method as follows:
1. introduce an initial discretization of the domain. t_j=jk , j>0 , x_i=ih ,0<i<n+1 where h and k are step sizes, h=1/n+1
2. select some simple FD schems to approximate the derivatives, for example

f'(x)=1/h[f(x+h)-f(x)]
f'(x)=1/2h[f(x+h)-f(x-h)]
f''(x)=1/h²[f(x+h)-2f(x)+f(x-h)]

So for our problem we get :

1/h²[v_i+1,j-2v_i,j+v_i-1,j]=1/k[v_i,j+1-v_i,j] ....(3)

when j=0 all the terms are known since we have g(xi,0)=v_i,0
to obtain v_i,1 we rewrite equation (3) as:

v_i,j+1=sv_i-1,j+(1-2s)v_i,j+sv_i+1,j where s=k/h².....(4)

Because equation (4) gives the values v_i,j+1explicitly in terms of the previous values,v_i-1,j,v_i,jand v_i+1,jthe method is called explicit method.

Stability Analysis

1. Matrix Method

We will consider the case when a(t)=b(t))=0. Equation (4) which defines the numerical process can be written using matrix notation.for this let the vector of values at time t=jk be denoted by V_jthen we get

V_j+1=AV_j where A is nxn matrix given by


                [1 - 2s       s          0  .....   0   ]
                [                                       ]
                [   s       1 - 2s       s   .....  0   ]
            A = [                                       ]
                [   0          s       1 - 2s       s   ]
                [                                       ]
                [   0          0          s  .... 1 - 2s]

Because a(t)=b(t)=0 we have v_0j=v_n+1,j=0
now since V_j+1=AV_j we have V_j=AV_j-1=A² V_j-2=....=A^jV₀.
from the fact that the temperature in the bar will be zero when when time goes to infinty we therefore can say that our numerical solution is also tending to zero as the time going to infinity. and also from the fact that limA^jV=0 as j gose to infinity is equivalent to have d(A)<1 where d(A) is the spectral radius of A. Therefore the parameter s/k² must be chosen so that d(A)<1. The eigenvalues of A are . c_j=1-2s(1-cos(a_j)) , where a_j=jpi/n+1 ,for 1<j<n.for more details about these eigenvalues please see Ref.1 and 2
For d(A) to be less than one we need
-1<1-2s(1-cosa)<1.
this is ture iff s<(1-cosa_j)^-1
since s is positive cosa_j=-1 and since a_j will be very close to pi when n=0 we must have s<1/2 this means for explicit algorithm to be stable we need to have s=k/h₂<1/2. Unfortunatly this restriction makes the method very slow because for example if h=0.01 then we must have k=5x10^-5,for 0<t<10 then the number of time steps must be 1/2x10⁶ and the number of mesh points must be over 20 million!!