Alkunopeus
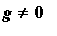
Tällöin D'Alembertin kaavassa tulee myös integraalitermi mukaan.
| > |
u:=(x,t)->1/2*(f(x+c*t)+f(x-c*t))+1/2/c*int(g(y),y=x-c*t..x+c*t);
|
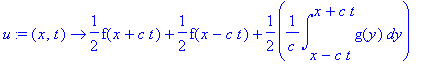
Sekä f että g ovat nyt parillisen jatkon 2L-jaksoisia jatkeita. Ongelmaksi tulee, että Maple ei mitenkään voi osata integroida JJ-operaattorin palauttamaa funktiota (proseduuria) symbolisesti. Numeerinen integrointi toki onnistuu. Jos halutaan symbolista, jaksollinen jatko pitää rakentaa sellaiseksi, että Maplen
int
osaa sitä käsitellä.
Ajatus: Välillä [-L,L] määritelty pariton laajennus kerrotaan välin karakterisitisella funktiolla (funktiolla, joka on 1, kun ollaan välillä ja 0 välin ulkopuolella). Tällaisia funktioita siirretään jakson monikerran verran vasemmalle ja oikealle ja lasketaan yhteen riittävän suureen n:n arvoon saakka. Näin saadaan jaksollinen jatke, jota Maple taatusti osaa integroida.
| > |
restart:with(plots):setoptions3d(orientation=[-30,50],axes=box):
#with(LinearAlgebra):
read("c:/usr/heikki/numsym05/maple/ns05.mpl");
# read("/p/edu/mat-1.192/ns05.mpl");
#read("/home/apiola/opetus/numsym/05/maple/ns05.mpl");
|
Warning, the name changecoords has been redefined
| > |
CHI:=(a,b,x)->H(x-a)-H(x-b); # Välin [a,b] karakteristinen funktio.
|
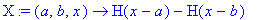
| > |
JaksJ:=(f,L,N,x)->sum(f(x+nnn*2*L)*CHI(-L,L,x+nnn*2*L),nnn=-N..N);
|
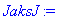
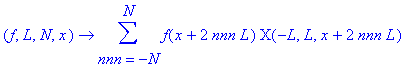
Esim:
| > |
f:=x->x*(1-x);plot(f,-1..1):
|
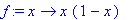
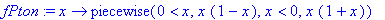
![[Maple Plot]](images/aaltoyhtalo_pohja30.gif)
| > |
ftahti:=x->JaksJ(fPton,1,10,x);
|

![[Maple Plot]](images/aaltoyhtalo_pohja32.gif)
Vrt:
| > |
plot(JJ(fPton,-1..1),-5..5);
|
![[Maple Plot]](images/aaltoyhtalo_pohja33.gif)
Kumpikin toimii, mutta JJ:llä tuotettua ei niin vain voida integroida symbolisesti. Sensijaan JaksJ:llä tuotettu voidaan ilman muuta integroida millä välillä vain
(kunhan huolehditaan siitä, että JaksJ:n kolmas argumentti N on ao. väliä ajatellen riittävän iso (piirrä, niin näet, mitä tarkoitan!)).
| > |
int(JaksJ(fPton,1,5,x),x=-2..0);
|
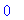
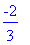
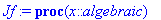
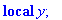
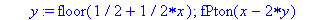

![PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0])](images/aaltoyhtalo_pohja40.gif)
![PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0])](images/aaltoyhtalo_pohja41.gif)
![PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0])](images/aaltoyhtalo_pohja42.gif)
![PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0])](images/aaltoyhtalo_pohja43.gif)
Numeerinen integrointi käy:
| > |
evalf(Int(Jf(x),x=-2..0));
|
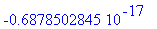
| > |
int(Jf(x),x=-2..0);evalf(%);
|
![int(PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0]),x = -2 .. 0)](images/aaltoyhtalo_pohja45.gif)
![int(PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0]),x = -2 .. 0)](images/aaltoyhtalo_pohja46.gif)
![int(PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0]),x = -2 .. 0)](images/aaltoyhtalo_pohja47.gif)
![int(PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0]),x = -2 .. 0)](images/aaltoyhtalo_pohja48.gif)
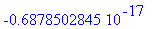
No nyt ei ole ongelmaa D' Alembert'n kaavan käytölle yleisessä muodossa.
Mallitehtävä:
Vaihdetaan edellisessä f:n ja g:n roolit. Ts. Alkuhetkellä kitaran kieli on lepotilassa, mutta alkunopeus on "kolmiomainen".
| > |
restart:with(plots):setoptions3d(orientation=[-30,50],axes=box):
#with(LinearAlgebra):
read("c:/usr/heikki/numsym05/maple/ns05.mpl");
# read("/p/edu/mat-1.192/ns05.mpl");
#read("/home/apiola/opetus/numsym/05/maple/ns05.mpl");
|
Warning, the name changecoords has been redefined
| > |
f:=x->0: g:=x->piecewise(x<L/2,x,x>L/2,L-x):L:=10:
|
| > |
plot(paritong(x),x=-20..20):
|
| > |
gtahti:=x->JaksJ(paritong,10,2,x):
|
| > |
plot(gtahti,-200..200); # Kun otettiin N=2 yllä, voidaan ajassa mennä yli 50:n, jotta gtahti(x-t) ja gtahti(x+t) laskevat oikein. Jos halutaan mennä sen yli on Jaksj:n 3:tta argumenttia N kasvatettava.
|
![[Maple Plot]](images/aaltoyhtalo_pohja50.gif)
Koska nyt f=0, D'Alembert'n kaavassa on vain integraalitermi:
| > |
u:=(x,t)->1/2/c*int(gtahti(y),y=x-c*t..x+c*t);
|
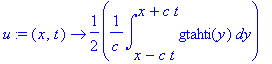
| > |
animate(u(x,t),x=0..10,t=0..20,frames=50,numpoints=300);
|
![[Maple Plot]](images/aaltoyhtalo_pohja52.gif)
| > |
plot3d(u(x,t),x=0..L,t=0..20,grid=[30,30]);
|
![[Maple Plot]](images/aaltoyhtalo_pohja53.gif)
Kuva tulee vielä havainnollisemmaksi, kun lisätään sopivia aika-arvoja vastaavat aaltomuodot, jolloin animaatiota on mukava verrata 3d-kuvaan.
| > |
display(pinta,seq(spacecurve([x,t,u(x,t),x=0..L],thickness=2,color=red),t=[0,1,10,20]));
|
![[Maple Plot]](images/aaltoyhtalo_pohja54.gif)
Jospa vilkaistaan u(x,t):n lauseketta. Aikamoinen taidonnäyte ohjelmalta, tällaisten hallitseminen käsin ei kyllä taitaisi onnistua.
Entä se JJ-tyyli, onnistuuko sittenkään?
| > |
gtahti2:=JJ(paritong,-10..10);
|
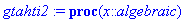
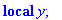
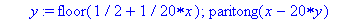

| > |
u2:=(x,t)->1/2/c*(evalf@Int)(gtahti2(y),y=x-c*t..x+c*t):
|
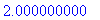
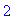
| > |
plot3d(u2(x,t),x=0..L,t=0..1);
|
![[Maple Plot]](images/aaltoyhtalo_pohja61.gif)
| > |
plot3d(u(x,t),x=0..L,t=0..1);
|
![[Maple Plot]](images/aaltoyhtalo_pohja62.gif)
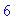
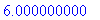
Error, (in evalf/int) unable to convert to pwlist
Kun ollaan sauvan puolenvälin lähellä, niin JJ-tyylillä tehty ei osaa laskea, kuten kuvastakin näkyy.
Siten tuo uusi summatyyli jaksolliseen jatkamiseen onkin ainoa toimiva näissä tehtävissä.
Huom! Mikään ei estä laskemasta sellaista tehtävää, jossa on sekä alkupoikkeutusta (f<>0) ja alkunopeutta (g<>0). Oppikirjoista nämä yleensä puuttuvat johtuen käsinlaskun vaivalloisuudesta, mutta sitä vaivaa meillä ei ole.
Ehdotus:
Kokeilkaa jotain esimerkkiä!
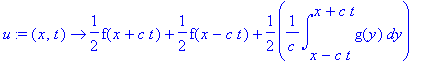
![]()
![[Maple Plot]](images/aaltoyhtalo_pohja4.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja5.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja6.gif)
![]()
![[Maple Plot]](images/aaltoyhtalo_pohja8.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja9.gif)
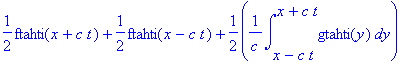
![[Maple Plot]](images/aaltoyhtalo_pohja13.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja18.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja20.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja21.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja22.gif)
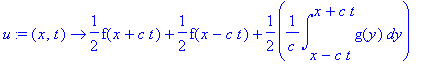
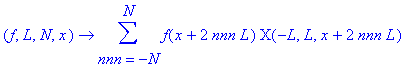
![[Maple Plot]](images/aaltoyhtalo_pohja30.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja32.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja33.gif)
![int(PIECEWISE([(x-2*floor(1/2+1/2*x))*(1-x+2*floor(1/2+1/2*x)), 0 < x-2*floor(1/2+1/2*x)],[(x-2*floor(1/2+1/2*x))*(1+x-2*floor(1/2+1/2*x)), x-2*floor(1/2+1/2*x) < 0]),x = -2 .. 0)](images/aaltoyhtalo_pohja45.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja50.gif)
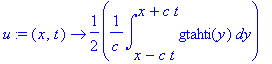
![[Maple Plot]](images/aaltoyhtalo_pohja52.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja53.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja54.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja61.gif)
![[Maple Plot]](images/aaltoyhtalo_pohja62.gif)