:n ominaisarvot ympyräsektorissa, Besselin funktiot

bessel.mws 4.5.05  HA

[Coo] Cooper: Intro to PDEs with Matlab

[Mol] Moler: Webbikirja: Ch 11 PDEs

[PDEtool] PDE toolbox, manuaali

[Coo] 8.4 Eigenfunctions for the disk  s. 315 alk.

Ominaisarvotehtävä:    , kun alueena on a-säteinen ympyrä, reunalla Dirichlet'n 0-RE:t.

Esitetään  napakoordinaatistossa ja suoritetaan muuttujanerottelu yritteellä  .

Tässä olemme kiinnostuneita ympyräsektorista, kaikilla reunoilla Dirichlet'n 0-RE:t. Olkoon sektorin keskuskulma = .

Tehtävä hoituu modifioimalla kiekkokäsittelyä sopivasti. Merkitään "yhteistä arvoa" :llä, tällä kertaa RE:t =>  .

Kun vielä suoritataan muuttujanvaihto (skaalaus):   , missä , saadaan :lle alla oleva Besselin diffyhtälö .

 toteuttaa yhtälön:      .

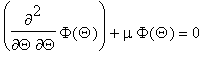>	restart:with(plots):

Warning, the name changecoords has been redefined

>	beta:=0.9: display(complexplot(exp(I*phi),phi=0..beta,view=[-.1..1.1,-.1..1]),complexplot(r*exp(I*beta),r=0..1),complexplot(r,r=0..1),axes=box,textplot([0.1,0.04,'beta'])); beta:='beta':

Erityisesti olemme kiinnostuneita seuraavasta:

>	beta:=3*Pi/2:  display(complexplot(exp(I*phi),phi=0..beta,view=[-1..1,-1..1]),complexplot(r*exp(I*beta),r=0..1),complexplot(r,r=0..1),axes=box); beta:='beta':

>	bessdy:=rho^2*diff(U(rho),rho,rho)+rho*diff(U(rho),rho)+(rho^2-mu)*U(rho)=0;

>

>

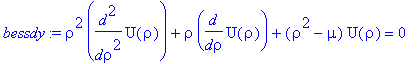
#?Bessel

>	dsolve(bessdy,U(rho));

BesselY:n kertoimeksi on otettava 0, koska se lähestyy , kun  .   Havainnollistetaan esimerkein (  ).

>	display(array([[plot(BesselJ(0.5,x),x=0..4),plot(BesselY(0.5,x),x=0.1..4)]]));

>	limit(BesselY(0.5,x),x=0,right);

>	#?BesselJZeros

>

>	#BesselJZeros(s, n1..n2)

>	#BJZ:=BesselJZeros(0.5, 0..10);

>	#display(plot([seq([BJZ[k],0],k=1..nops([BJZ]))],style=point,symbol=circle,symbolsize=20,color=black),plot(BesselJ(0.5,x),x=0..32));

 - yhtälöstä ja sektorin janareuna-arvoista (0), seuraa:

>	Phi:=Theta->sin(sqrt(mu)*Theta);  # missä

>	sqrt(mu)=n*Pi/beta;

Merkitään , eli  .

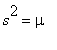Otetaan tapaus: yksikköympyrän sektori: 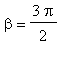, Dirichlet-RE't  Tarkoitus on approksimoida L-alueen ominaisarvoja ja -funktioita.

>	beta:=3*Pi/2; s:=n->n*Pi/beta;  Phi:='Phi':

Jotta 0-RE toteutuisi a-säteisellä sektorin kaarella, on oltava R(a)=0, ts. , ts , joka tarkoittaa

Besselin funktion nollakohtaa numero . Tästäpä saadaan tehtävän ominaisarvot  .

>

>	rho:=(n,M)->BesselJZeros(s(n), 1..M);

>	#rho(1,10);evalf(%);

>	#evalf(BesselJZeros(s(1), 1..10));

>	#evalf(lam(1,10));

>	#sort([evalf(seq(lam(n,20),n=1..20))]);

>

#?sort

>	#L[1]:=[evalf(rho(1,100))]: L[1][1..4];

>	for n to 10 do   Rho[n]:=[evalf(rho(n,100))]; end do: n:='n':

>

>	#map(z->z^2,Rho[2][1..10]);

>	#Rho[4][1..5];

Pyritään approksimoimaan L-alueen ominaisarvoja yllä olevan "L-sektorin" ominaisarvoilla. Valitaan ympyrän säde niin, että pinta-alat samat

>	3=3/4*Pi*sade^2; solve(%,sade);

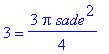
>	a:=2/sqrt(Pi);

>	ominarvot:=map(z->evalf((z/a)^2),sort(map(op,[seq(Rho[n],n=1..10)]))):

>	#Rho[7][1..5];

>	ominarvot[1..10];

No nythän osuvat ihan kohdalleen

>

>	R:=(m,n,r)->BesselJ(s(n),r*(Rho[n][m])/a);

>	evalf(R(2,3,2));

>	phi:=(m,n,r,Theta)->R(m,n,r)*sin(s(n)*Theta); lambda:=(m,n)->evalf((Rho[n][m]/a)^2);

>	m:='m':n:='n':

>	lambda(m,n),phi(m,n,r,t);

>	lambda(3,2);

>

>	addcoords(z_cylindrical,[z,theta,r],[r*cos(theta),r*sin(theta),z]);

Warning, coordinates already exists, system redefined.

>	m:=1:n:=1:lambda(m,n);plot3d(phi(m,n,r,Theta),Theta=0..3*Pi/2,r=0..1,coords=z_cylindrical,orientation=[-132,71],axes=BOXED,scaling=constrained,style=patchcontour);

>	m:=2:n:=1:lambda(m,n);plot3d(phi(m,n,r,Theta),Theta=0..3*Pi/2,r=0..1,coords=z_cylindrical,orientation=[-132,71],axes=BOXED,scaling=constrained,style=patchcontour);

>	m:=1:n:=2:lambda(m,n);plot3d(phi(m,n,r,Theta),Theta=0..3*Pi/2,r=0..1,coords=z_cylindrical,orientation=[-132,71],axes=BOXED,scaling=constrained,style=patchcontour);

>	m:=2:n:=2:lambda(m,n);plot3d(phi(m,n,r,Theta),Theta=0..3*Pi/2,r=0..1,coords=z_cylindrical,orientation=[-132,71],axes=BOXED,scaling=constrained,style=patchcontour);

>	m:=1:n:=3:lambda(m,n);plot3d(phi(m,n,r,Theta),Theta=0..3*Pi/2,r=0..1,coords=z_cylindrical,orientation=[-132,71],axes=BOXED,scaling=constrained,style=patchcontour);

>	m:=2:n:=3:lambda(m,n);plot3d(phi(m,n,r,Theta),Theta=0..3*Pi/2,r=0..1,coords=z_cylindrical,orientation=[-132,71],axes=BOXED,scaling=constrained,style=patchcontour);

>

Nähdään, että n:n mukaan alue jakaantuu n:ään sektoriin, missä n määrää Besselin funktion kertaluvun s(n)..

Kuvat ovat samanlaiset kuin Molerissa s. 11 sarakejärjestyksessä katsotut. Myös ominaisarvot ovat tarkalleen samat, joten kaikki meni hienosti.

Tässä eivät ole kaikki ominaisarvot suuruusjärjestyksessä, vaan siinä on pelissä kolmen alimman Besselin funktion kaksi ensimmäistä nollakohtaa.

Esim.

>	lambda(1,4);

Tässä on 20 ekaa suuruusjärjestyksessä:

>	ominarvot[1..20];

Tästä on hyvä lähteä L-alueen käsittelyyn Molerin tyyliin.