Numeerinen ja symbolinen laskenta
Harjoitus 6
Heikki Apiola ja Mika Juntunen
Alustukset
| > |
alustukset:=proc()
local polku,ns05;
#ns05:="/p/edu/mat-1.192/ns05.mpl");
#ns05:="c:/usr/heikki/numsym05/maple/ns05.mpl";
ns05:="/home/apiola/opetus/numsym/05/maple/ns05.mpl";
#polku:="c:/MATLAB6p1/work/":
#polku:="/tmp/":
#datafile:=cat(polku,"hab.txt");
with(plots):setoptions3d(orientation=[-30,50],axes=box):
read(ns05);
#with(LinearAlgebra);
end proc:
|
Tämä kannattaa sijoittaa eri työarkille, niin on tehty:
H/alustukset.mws
Tällöin on helppo käydä
restart
:n jälkeen napsauttamassa alustukset päälle.
Tehtävä 1
(a)
| > |
restart: # Nyt on käytävä määrittelemässä alustukset();
|
| > |
bn:=2/L*Int(f(x)*sin(n*Pi*x/L),x=0..L);
|
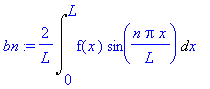
| > |
L:=Pi; # asetetaan L=Pi
bn;
|
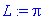
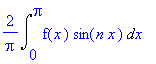
Osittaisintegroidaan
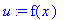

| > |
du:=Diff(f(x),x);
v:=int(dv,x);
|
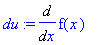
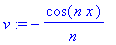
| > |
Int(u*dv,x=0..L)
=-Int(du*v,x=0..L) + subs(x=Pi,u*v) -subs(x=0,u*v);
|
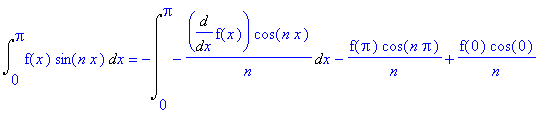
Osittaisintegroidaan uudestaan
| > |
u2:=Diff(f(x),x); dv2:=cos(n*x)/n;
|
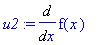
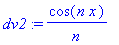
| > |
du2:=Diff(u2,x); v2:=int(dv2,x);
|
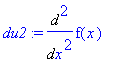
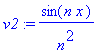
| > |
Int(u*dv,x=0..L)
=-Int(du2*v2,x=0..L) +subs(x=Pi,u2*v2) -subs(x=0,u2*v2)
+subs(x=Pi,u*v) -subs(x=0,u*v);
|
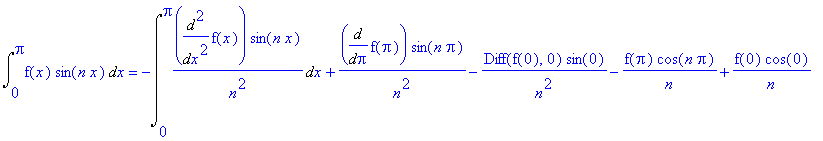
| > |
Int(u*dv,x=0..L)
=-Int(du2*v2,x=0..L) +subs(x=Pi,u*v) +f(0)/n;
|
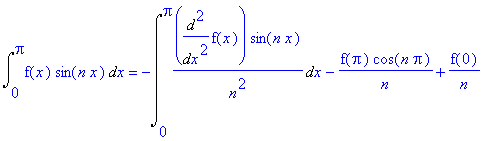
Koska parittoman jatkuvan funktion on oltava 0:ssa 0 ja samoin 2L-jaksoisen parittoman jatkuvan on oltava L:ssä 0, niin sijoitustermit häviävät.
Olkoon
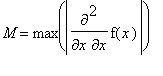 . M on äärellinen, koska
. M on äärellinen, koska
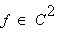
.
Siis
![b[n] < 2/pi*M*pi/(n^2)](images/harjoitus617.gif)
eli
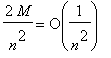 .
.
Tämä on varmaankin vaivattomampi laskea käsin, mutta harjoiteltiinpa samalla hieman Maple-tekstinkäsittelyä.
(Tähän ei kannata paljon panostaa, mutta tekstimuotoisen Maple-syntaksia noudattavan lausekkeen voi helposti muuntaa matemaattiseen muotoon maalaamalla ja painamalla maalatun päällä hiiren oikeaa, josta -> convert -> standard math.)
Esim yllä oleva C^2:een kuuluminen kirjoitettiin näin: f in C^2 , joka hiirellä konvertoitiin.
(b)
| > |
#read("/p/edu/mat-1.192/ns05.mpl");
#read("c:/usr/heikki/numsym05/maple/ns05.mpl");
#read("/home/apiola/opetus/numsym/05/maple/ns05.mpl");
|
| > |
bn:=2/L*Int(f(x)*sin(n*Pi*x/L),x=0..L);
|
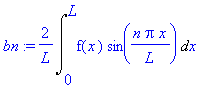
| > |
f:=x->piecewise(x<L/2,x,x>L/2,L-x);
|
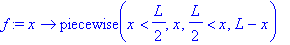
| > |
kuva1:=plot(subs(L=2,f(x)),x=0..2,color=blue):
kuva2:=plot(subs(L=2,D(f)(x)),x=0..2,color=black):
display(kuva1,kuva2);
|
![[Maple Plot]](images/harjoitus621.gif)
| > |
bn:=2/L*(int(x*sin(n*Pi*x/L),x=0..L/2)+int((L-x)*sin(n*Pi*x/L),x=L/2..L));
|
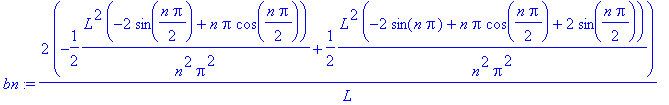
| > |
b[n]:=trigsiev(bn,n); abs('b[n]') < subs(sin(n*Pi/2)=1,%);
#Tekstinkäisttelyä.
|
![b[n] := 4*L*sin(1/2*n*Pi)/n^2/Pi^2](images/harjoitus623.gif)
![abs(b[n]) < 4*L/n^2/Pi^2](images/harjoitus624.gif)
(c)
| > |
restart: #alustukset(); # eri ws:llä
|
Järkevintä olisi laittaa tiedoston nimi polkuineen
sinSkertoimet
-funktion argumentiksi, jolloin polkumuutokset tehtäisiin yllä olevissa alustuskomennoissa, eikä tarvitsisi kajota funktion koodiin. Itse asiassa
näin on tehty
, mutta vanhatkin funktiot ovat jäljellä.
Uusi funktio on nimeltään
sinikertoimet
.
Yllä olevaa voi käyttää hyödyksi nyt haluttaessa lukea Mapleen dataa. Tyypillisesti on tehty raskas laskentaoperaatio,
vaikka 1000 sinisarjan kerrointa. Kun niitä tarvitaan uudestaan, kannattaa lukea tiedostosta:
kertoimet:=readdata(datafile,1):
Jos tarvitaan vain Maplesta Mapleen, niin voidaan käyttää save/read-yhdistelmää, kts alla.
| > |
N:=100;
L:=10;
f:=x->sin(Pi*x/5)*exp(x/2);
|
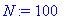
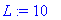
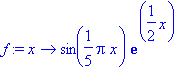
| > |
plot(ParitonJ(f),-10..10);Jpf:=JJ(ParitonJ(f),-10..10);
|
![[Maple Plot]](images/harjoitus628.gif)
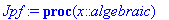
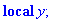
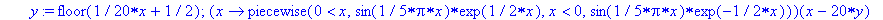

| > |
#plot(ParitonJ(f),-0.1..0.1);
|
| > |
plot(Jpf,-20..20);plot(Jpf,-2..2);
|
![[Maple Plot]](images/harjoitus633.gif)
![[Maple Plot]](images/harjoitus634.gif)
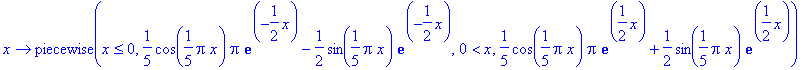
| > |
plot(D(ParitonJ(f)),-1..2);plot(D(D(ParitonJ(f))),-1..2);
|
![[Maple Plot]](images/harjoitus636.gif)
![[Maple Plot]](images/harjoitus637.gif)
Pariton jatke on siis
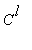 , mutta ei
, mutta ei
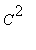 .
.
| > |
bn:=sinikertoimet(f,L,N,bfile): # Talletetaan tiedostoon.
|
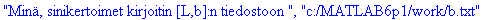
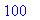
Tässä pieni sivujuonne:
save/read -- muuttujien talletus tiedostoon
| > |
B:='B': # B:n tyhjennys
|
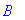
![[10., -14.86135515, 25.45304893, -18.67536387, 9.493114283]](images/harjoitus643.gif)
Kaikenlaista muutakin voidaan tallettaa:
| > |
f:=x->x^2: g:=D(f): a:=[1,2,3]:save f,g,a, afile;
|
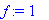
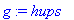
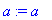
| > |
read afile;
f(x), g(t), a;
|
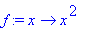

![a := [1, 2, 3]](images/harjoitus649.gif)
![x^2, 2*t, [1, 2, 3]](images/harjoitus650.gif)
Pääjuoni jatkuu...
![[-14.86135515, 25.45304893, -18.67536387]](images/harjoitus651.gif)
| > |
# ns05.,pl:ssä on myös Matlab-henkinen piirtofunktio matlabplot.
|
| > |
X:=map( ln,[seq(i,i=1..N)] ):
|
| > |
Y:=map(ln, map(abs,bn)):
|
| > |
kuva1:=matlabplot(X,Y1,color=black):
|
| > |
kuva2:=plot(-2*x,x=0..max(op(X)),color=red):
|
| > |
kuva3:=plot(-3*x,x=0..max(op(X)),color=blue):
|
| > |
display(kuva1,kuva2,kuva3);
|
![[Maple Plot]](images/harjoitus652.gif)
Katsotaan kuvasta hiiren avulla, mikä vakio suunnilleen pitää mustasta käyrästä vähentää, että tullaan siniselle. => hiukan alle 7.
| > |
kuva4:=matlabplot(X,Y4,'black'):
|
| > |
display(kuva1,kuva2,kuva3,kuva4);
|
![[Maple Plot]](images/harjoitus653.gif)
Hyvinpä selvästi näkyy
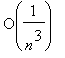 - käytös.
- käytös.
Nähtiin, että sileä funktio, jonka pariton jatko on vain
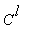 voi antaa Fourier-kertoimille jopa
voi antaa Fourier-kertoimille jopa
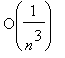 - käytöksen.
- käytöksen.
Asian systemaattinen tutkimus jääköön tällä erää.
Tehtävä 2
| > |
alustukset(); # Tee alustukset.mws-työarkilla
|
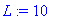
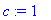
| > |
f:=x->-sin(Pi*x/5)*exp(x/2);
|
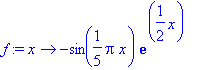
| > |
u:=lamposini(f,L,c,N,bfile):
|
| > |
plot3d(u(x,t),x=0..10,t=0..10,axes=boxed);
|
![[Maple Plot]](images/harjoitus661.gif)
Vaihtoehtoinen tapa, readdata:n käyttö suoraan
Oikeastaan koko
lamposini
-funktion sisältö on tämä kaava:
| > |
S:=(x,t,N)->add(b[n]*sin(n*Pi*x/L)*exp(-lambda(n)^2*t),n=1..N);
|
![S := proc (x, t, N) options operator, arrow; add(b[n]*sin(n*Pi*x/L)*exp(-lambda(n)^2*t),n = 1 .. N) end proc](images/harjoitus662.gif)
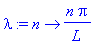
Ajatellaan, että b-kertoimet on kirjoitettu tiedostoon, jonka nimi polkuineen on muuttujassa
datafile
.
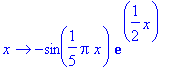
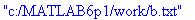
Tehdään nyt se kirjoittaminen (eikä vain ajatella tehdyksi,vrt.yllä).
| > |
sinikertoimet(f,L,N,bfile):
|
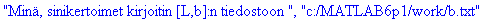
| > |
L:=Lb[1]: b:=Lb[2..-1]:
|
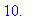
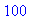
| > |
plot3d(S(x,t,50),x=0..10,t=0..10);
|
![[Maple Plot]](images/harjoitus669.gif)
Määritellään grafiikkafunktio, jonka avulla on joustavaa tarkkailla ratkaisua eri aika-alueilla. (Kun ei voida lokalisoida, käytetään edes hiukan kummallisia muuttujan nimiä.)
| > |
kuva:=(N,tvali::range)->plot3d(S(xxx,ttt,N),xxx=0..10,ttt=op(1,tvali)..op(2,tvali));
|
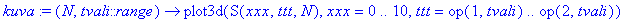
| > |
kuva(15,0.1..10);kuva(15,0..0.1);
|
![[Maple Plot]](images/harjoitus671.gif)
![[Maple Plot]](images/harjoitus672.gif)
| > |
display(seq(kuva(N,0..0.1),N=[3,5,7,9,11,13,15]),insequence=true);
|
![[Maple Plot]](images/harjoitus673.gif)
| > |
display(seq(kuva(15,0..t),t=[seq(kk*0.1,kk=2..50)]),insequence=true);
|
![[Maple Plot]](images/harjoitus674.gif)
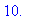
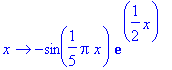
| > |
Nmax:=100; t0:=0.1; Tol:=1e-6;
|
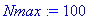
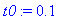
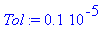
| > |
#bn:=sinikertoimet(f,L,Nmax):
|
| > |
Lb:=readdata(bfile,1):L:=Lb[1]: b:=Lb[2..-1]:
|
![[14.86135515, -25.45304893, 18.67536387]](images/harjoitus680.gif)
Virhearvio:
| > |
e:=(t,N,L,maxbn)->maxbn*evalf(exp(-(N*Pi/L)^2*t)/(1-exp(-N*(Pi/L)^2*t)));
|
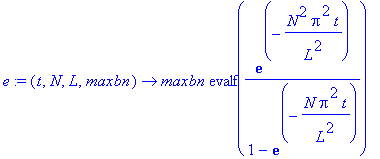
| > |
plot([seq([n,abs(b[n])],n=1..nops(b))],view=[0..50,0..2]);
|
![[Maple Plot]](images/harjoitus682.gif)
Tällä perusteella voidaan ottaa maxbn=b[N].
Toki maxbn saataisin helposti näin:
| > |
# max(seq
(abs(b[k]), k=N..Nmax) :
|
Otetaan malliksi 2 tapausta: (1) Pieni t0 ja (2) suuri t0.
On selvää, että virhe pienenee dramaattisesti, kun t kasvaa.
(1)
Pieni t0
| > |
seq(e(t0,m,L,b[m]),m=2..11);
|
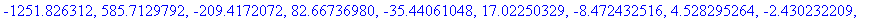
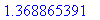
| > |
S:=(x,t,N)->add(b[n]*sin(n*Pi*x/L)*exp(-lambda(n)^2*t),n=1..N);
|
![S := proc (x, t, N) options operator, arrow; add(b[n]*sin(n*Pi*x/L)*exp(-lambda(n)^2*t),n = 1 .. N) end proc](images/harjoitus685.gif)
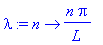
Verrataan virhearviota ja "todellista" virhettä. Viime mainittu saadaan pitämällä lukua N=100 "äärettömänä". Piirretään ja haetaan hiirellä maksimiarvo ja sijoitetaan saatu lukema virheen arvoksi muuttujaan
maxvirhe[...].
| > |
plot(abs(S(x,t0,100)-S(x,t0,10)),x=0..L);
|
![[Maple Plot]](images/harjoitus687.gif)
![maxvirhe[.1,10] := .35](images/harjoitus688.gif)
| > |
virhearvio[t0,10]:=e(t0,11,L,b[11]);
|
![virhearvio[.1,10] := 1.368865391](images/harjoitus689.gif)
Tehdään sama, kun otetaan 20 termiä. Jotta kuvan asteikkonumerot riittäisivät, skaalataan kertomalla 100:lla, joka sitten jaetaan pois.
| > |
plot(100*abs(S(x,t0,100)-S(x,t0,20)),x=0..L);
|
![[Maple Plot]](images/harjoitus690.gif)
| > |
maxvirhe[t0,20]:=0.19/100;
|
![maxvirhe[.1,20] := .1900000000e-2](images/harjoitus691.gif)
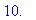
| > |
virhearvio[t0,20]:=e(t0,21,L,b[21]);
|
![virhearvio[.1,20] := .4526261720e-2](images/harjoitus693.gif)
Nyt täytyy kertoa 10000:lla, jotta asteikkolukuja näkyisi.
| > |
plot(10000*abs(S(x,t0,100)-S(x,t0,30)),x=0..L);
|
![[Maple Plot]](images/harjoitus694.gif)
| > |
maxvirhe[t0,30]:=0.03/10000;
|
![maxvirhe[.1,30] := .3000000000e-5](images/harjoitus695.gif)
| > |
virhearvio[t0,30]:=e(t0,31,L,b[31]);
|
![virhearvio[.1,30] := .5879050397e-5](images/harjoitus696.gif)
| > |
yhteenveto[t0]:=seq([n,maxvirhe[t0,n],virhearvio[t0,n]],n=[10,20,30]);
|
![yhteenveto[.1] := [10, .35, 1.368865391], [20, .1900000000e-2, .4526261720e-2], [30, .3000000000e-5, .5879050397e-5]](images/harjoitus697.gif)
| > |
't0'=t0; # Vain tekstiä varten.
|
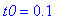
| > |
'N',cat("todellinen ", "maxvirhe"), maxvirhearvio; # Otsikkoteksti
|

| > |
Matrix([yhteenveto[t0]]);
|
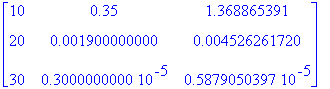
Virhearvion avulla voitaisiin rakentaa seuraavanlainen silmukka, jonka avulla taataan riittävä määrä termejä tietyllä ajanhetkellä.
(Voitaisi kirjoittaa proseduuriksi, mutta antaa nyt toistaiseksi olla "kertakäyttökoodina",
jota leikataan/liimataan.)
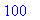
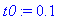
| > |
err:=2*Tol+1:
N:=1:
while err>Tol do
N:=N+1;
if N=Nmax then
print("Tarvitaan lisää termejä");
break;
end if;
err:=evalf(e(t0,N+1,L,abs(b[N+1])));
print(N+1,err);
end do:
|
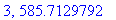
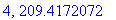

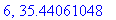
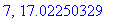
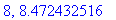
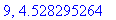
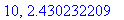
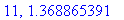
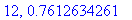
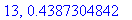
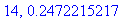
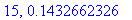
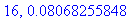
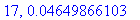
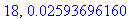
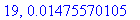
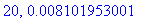
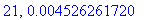
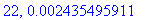
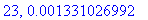
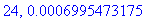
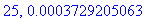
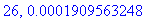
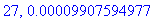
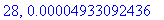
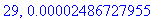
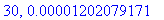

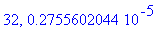
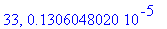
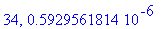
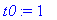
| > |
err:=2*Tol+1:
N:=1:
while err>Tol do
N:=N+1;
if N=Nmax then
print("Tarvitaan lisää termejä");
break;
end if;
err:=evalf(e(t0,N+1,L,abs(b[N+1])));
print(N+1,err);
end do:
|
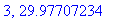
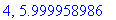
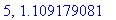
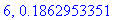
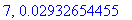
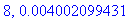
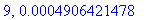
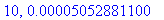

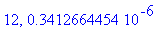
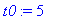
| > |
err:=2*Tol+1:
N:=1:
while err>Tol do
N:=N+1;
if N=Nmax then
print("Tarvitaan lisää termejä");
break;
end if;
err:=evalf(e(t0,N+1,L,abs(b[N+1])));
print(N+1,err);
end do:
|
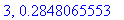
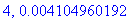
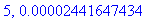
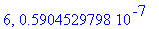
Näppärästi nähdään, että tämän enempää ei ainakaan kannata ruutia tuhlata termien lukumäärän suhteen.
Tässä tuli samalla niin pienet kuin suuretkin t0:t.
Tehtävä 3
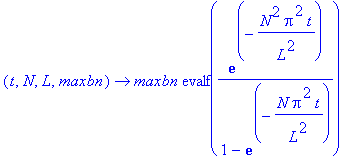
Kirjoitetaan em. koodi proc:ksi:
| > |
annaLkm:=proc(b,Nmax,t0,Tol,L)
local err,N;
err:=2*Tol+1:
N:=1:
while err>Tol do
N:=N+1;
if N=Nmax then
print("Tarvitaan lisää termejä");
break;
end if;
err:=evalf(e(t0,N+1,L,abs(b[N+1])));
end do:
RETURN(N+1);
end proc:
|
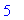
| > |
T:=[0.2, 0.1, 0.05, 0.025, 0.01];
|
![T := [.2, .1, .5e-1, .25e-1, .1e-1]](images/harjoitus6153.gif)
| > |
seq(annaLkm(b,Nmax,T[i],Tol,L),i=1..5);
|
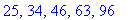
Näiden kanssa jatketaan Matlabissa.
Tehtävä 4
| > |
alustus(): # mene työarkille alustus.mws ja tee siellä
|
| > |
G:=t->t/(1+t)+t*exp(-t/5):
|
| > |
Limit(G(t),t=infinity): %=value(%);
|
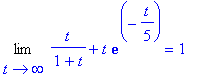
![[Maple Plot]](images/harjoitus6156.gif)
Ajanhetkellä t=100 ollaan jo aika lähellä 1:tä. (G:llä on minimi suunnilleen 48:ssa ja siitä noustaan hyvin hitaasti kohti 1:tä.)
![[Maple Plot]](images/harjoitus6157.gif)
| > |
T:=linspace(30,500,50): map(G,T);
|
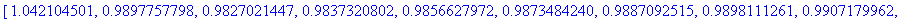
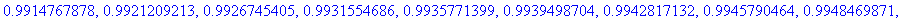
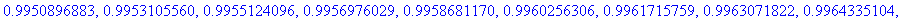
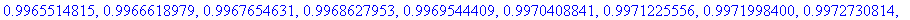
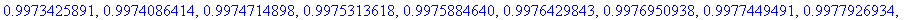
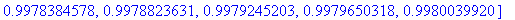
Varsinainen homma Matlabissa, analyyttinen harj7:ssä.
Tehtävä 5
| > |
alustus(): # mene ao. työarkille!
|
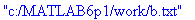
Määritellään funktiot (proseduurit)
kosinikertoimet
ja
lampokosini
vastaavien "siniserkkujen" tyyliin:
| > |
L:=10; c:=1; N:=20;
f:=x->exp(-(x-5)^2);
|
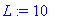
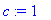
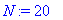
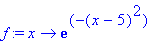
| > |
u:=lampokosini(f,L,c,N,afile):
|

| > |
plot3d(u(x,t),x=0..10,t=0..10,axes=boxed);
|
![[Maple Plot]](images/harjoitus6170.gif)
| > |
ka:=evalf( int(f(x),x=0..10) ) / L;
|
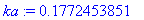
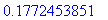
Tämä on vakioarvo, jota ratkaisu lähestyy, sarjahan on muotoa
![a[0]+sum(a[n]*cos(n*Pi*x/L)*exp(-k*lambda[n]^2*t))](images/harjoitus6175.gif) .
.
Summalauseke -> 0, kun t->
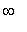 . Siispä sarja ->
. Siispä sarja ->
![a[0]](images/harjoitus6177.gif) , joka on juuri tuo integraali (funktion keskiarvo välillä [0,L]).
, joka on juuri tuo integraali (funktion keskiarvo välillä [0,L]).
Siispä vakiofunktio u = 0.17724 on "steady state"-ratkaisu.
| > |
U:=seq(u(j*1,10),j=0..10):
max(U); min(U);
|
Homogeeniset Neumann RE:t eivät päästä lämpöä karkaamaan, joten lämpömäärä pysyy samana
mutta se jakautuu tasaisesti koko alueelle.
Itse asiassa Maple osaa integroida "analyyttisesti", erf-funktion avulla:
| > |
int(f(x),x=0..10); evalf(%);
|
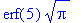
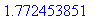
Tehtävä 6
| > |
osdy:=c^2*diff(u(x,t),x$2)=diff(u(x,t),t);
eval(subs(u(x,t)=F(x)*G(t), osdy));
|
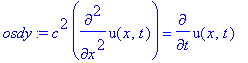
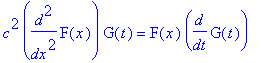
| > |
separoitu:=simplify(%/(c^2*F(x)*G(t)));
|
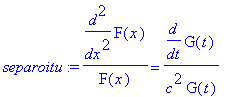
| > |
xyht:=lhs(separoitu)=-p^2;
tyht:=rhs(separoitu)=-p^2;
|
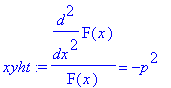
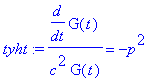
| > |
FDY:=lhs(xyht)*F(x)=rhs(xyht)*F(x);
|
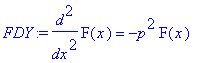
| > |
GDY:=c^2*lhs(tyht)*G(t)=c^2*rhs(tyht)*G(t);
|
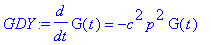
| > |
ff:=rhs(dsolve(FDY,F(x)));
dsolve(GDY,G(t)): gg:=rhs(%);
|
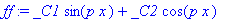
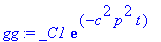
| > |
coeff(ff,sin(p*x)); # Tämä on varmempi tapa kuin subs(C_1=...),koska Maple saattaa eri ajoissa muuttaa järjestystä. (Jos käytät em. tapaa, niin tarkkaile!) Tehdään tässä varman päälle. (Silloin, kun on vain yksi kerroin, ei vaaraa ole.)
|
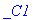
| > |
ff:=subs(coeff(ff,sin(p*x))=0,ff); # koska u_x(0,t)=0
gg:=subs(_C1=1,gg); # Kantafunktion kertoimeksi kelpaa luku 1.
|
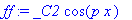
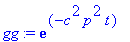
| > |
ehto2:=diff(ff,x)+h*ff=0;
|
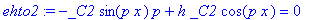
| > |
ehto2:=subs({_C2=1,x=L},ehto2);
|
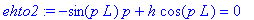
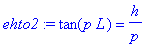
Asettamalla p=sqrt(\lambda) ja s=pL, saadaan
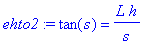
| > |
kuva1:=plot([tan(s),L*h/s],s=1..20,y=0..10,discont=true,color=[blue,red]):
|
![[Maple Plot]](images/harjoitus6196.gif)
| > |
fsolve(ehto2,s=0..Pi/2);
|
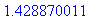
Leikkauspisteet ovat väleillä
![[n*pi, n*pi+pi/2]](images/harjoitus6198.gif) , koska leikkauspisteessä 0 < tan(s) <
, koska leikkauspisteessä 0 < tan(s) <
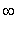
| > |
S:=[seq(fsolve(ehto2,s=n*Pi..n*Pi+Pi/2),n=0..10)];
|
![S := [1.428870011, 4.305801413, 7.228109772, 10.20026259, 13.21418568, 16.25936123, 19.32703429, 22.41084833, 25.50638299, 28.61058194, 31.72131067]](images/harjoitus6200.gif)
![S := [1.428870011, 4.305801413, 7.228109772, 10.20026259, 13.21418568, 16.25936123, 19.32703429, 22.41084833, 25.50638299, 28.61058194, 31.72131067]](images/harjoitus6201.gif)
| > |
display(kuva1,plot([seq([S[k],tan(S[k])],k=1..nops(S))],style=point,symbol=cross,symbolsize=20,color=black));
|
![[Maple Plot]](images/harjoitus6202.gif)
![lambda := proc (n) options operator, arrow; S[n]^2/L^2 end proc](images/harjoitus6203.gif)
Ominaisarvot:
| > |
seq(lambda(k),k=1..nops(S));
|
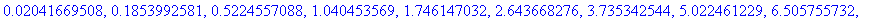
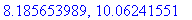
Ominaisfunktiot:
| > |
X:=(x,n)->cos(sqrt(lambda(n))*x);
|
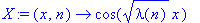
| > |
plot([seq(X(x,n),n=1..3)],x=0..10);plot([seq(X(x,n),n=4..7)],x=0..10);
|
![[Maple Plot]](images/harjoitus6207.gif)
![[Maple Plot]](images/harjoitus6208.gif)
| > |
plot([seq(X(x,n),n=1..nops(S))],x=0..10);
|
![[Maple Plot]](images/harjoitus6209.gif)
Paras visualisointi tuosta röykkiöstä syntyy animoiden:
| > |
kuva:=n->plot(X(x,n),x=0..10);
|
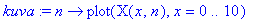
| > |
display(seq(kuva(n),n=1..nops(S)),insequence=true);
|
![[Maple Plot]](images/harjoitus6211.gif)
Tarkkaile reunoja: Oikeassa reunassa funktion arvon pitäisi olla derivaatan arvon vastaluku. Kyllä se siltä näyttää.Vasemmassa reunassa derivaatta = 0.
(Funktion arvo on sattumoisin 1 (koska cos(0)=1), mutta se ei ole reunaehto.)
Kirjoitetaan ominaisarvot vielä tiedostoon.
| > |
writedata(afile,[seq(lambda(k),k=1..nops(S))]);
|
Tähän liittyvä jatkotehtävä voidaan kehittää harjoitukseen 7.
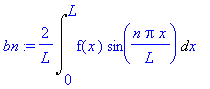
![]()
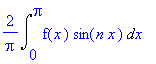
![]()
![]()
![]()
![]()
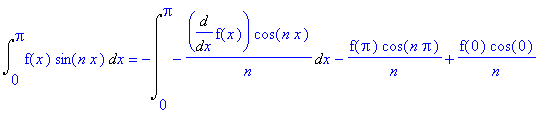
![]()
![]()
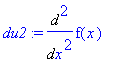
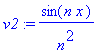
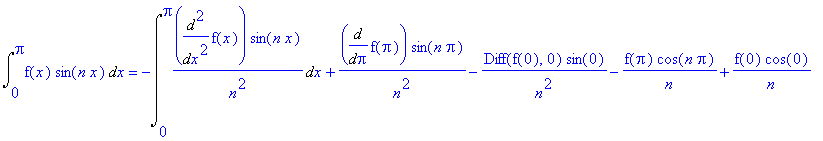
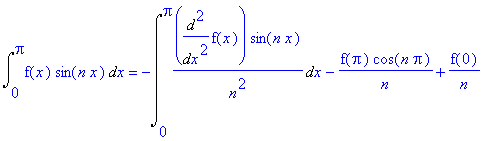
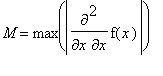 . M on äärellinen, koska
. M on äärellinen, koska
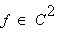
![b[n] < 2/pi*M*pi/(n^2)](images/harjoitus617.gif)
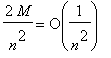 .
.
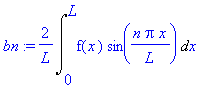
![]()
![[Maple Plot]](images/harjoitus621.gif)
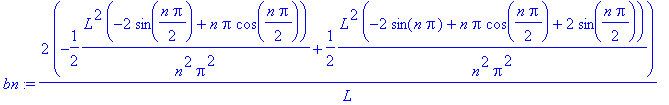
![b[n] := 4*L*sin(1/2*n*Pi)/n^2/Pi^2](images/harjoitus623.gif)
![abs(b[n]) < 4*L/n^2/Pi^2](images/harjoitus624.gif)
![]()
![]()
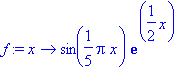
![[Maple Plot]](images/harjoitus628.gif)
![]()
![]()
![]()
![]()
![[Maple Plot]](images/harjoitus633.gif)
![[Maple Plot]](images/harjoitus634.gif)
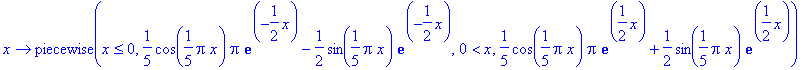
![[Maple Plot]](images/harjoitus636.gif)
![[Maple Plot]](images/harjoitus637.gif)
![]() , mutta ei
, mutta ei
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Maple Plot]](images/harjoitus652.gif)
![[Maple Plot]](images/harjoitus653.gif)
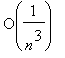 - käytös.
- käytös.
![]() voi antaa Fourier-kertoimille jopa
voi antaa Fourier-kertoimille jopa
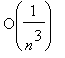 - käytöksen.
- käytöksen.
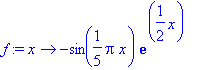
![[Maple Plot]](images/harjoitus661.gif)
![S := proc (x, t, N) options operator, arrow; add(b[n]*sin(n*Pi*x/L)*exp(-lambda(n)^2*t),n = 1 .. N) end proc](images/harjoitus662.gif)
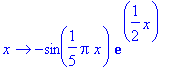
![[Maple Plot]](images/harjoitus669.gif)
![[Maple Plot]](images/harjoitus671.gif)
![[Maple Plot]](images/harjoitus672.gif)
![[Maple Plot]](images/harjoitus673.gif)
![[Maple Plot]](images/harjoitus674.gif)
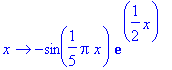
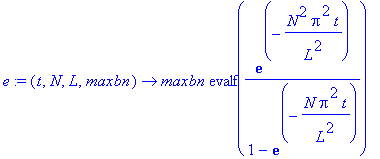
![[Maple Plot]](images/harjoitus682.gif)
![S := proc (x, t, N) options operator, arrow; add(b[n]*sin(n*Pi*x/L)*exp(-lambda(n)^2*t),n = 1 .. N) end proc](images/harjoitus685.gif)
![[Maple Plot]](images/harjoitus687.gif)
![[Maple Plot]](images/harjoitus690.gif)
![[Maple Plot]](images/harjoitus694.gif)
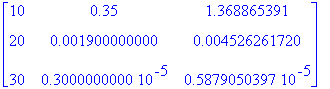

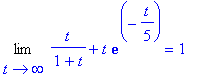
![[Maple Plot]](images/harjoitus6156.gif)
![[Maple Plot]](images/harjoitus6157.gif)
![[Maple Plot]](images/harjoitus6170.gif)
![a[0]+sum(a[n]*cos(n*Pi*x/L)*exp(-k*lambda[n]^2*t))](images/harjoitus6175.gif) .
.
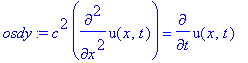
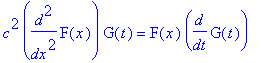
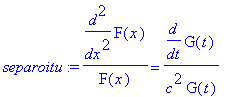
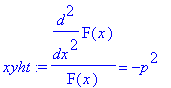
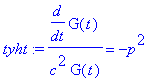
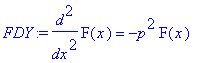
![[Maple Plot]](images/harjoitus6196.gif)
![[n*pi, n*pi+pi/2]](images/harjoitus6198.gif) , koska leikkauspisteessä 0 < tan(s) <
, koska leikkauspisteessä 0 < tan(s) <
![[Maple Plot]](images/harjoitus6202.gif)
![lambda := proc (n) options operator, arrow; S[n]^2/L^2 end proc](images/harjoitus6203.gif)
![[Maple Plot]](images/harjoitus6207.gif)
![[Maple Plot]](images/harjoitus6208.gif)
![[Maple Plot]](images/harjoitus6209.gif)
![[Maple Plot]](images/harjoitus6211.gif)