Mat-1.192 Numeric and symbolic computing
Tammikuu 2004/Jan 2004
Maple-perusteita/basics, ...maple/perusteita.mws (.html)
Language will be sometimes English, sometimes Finnish for the time being. Stabilizes, when the course starts according to the participants' nationalities.
Course directory for Maple instructions and codes:
www.math.hut.fi/teaching/numsym/04/maple/
Abbreviation:
.../maple/
Varsinainen
toiminta alkaa kohdasta 6
, lue kuitenkin ainakin 1 läpi huolella.
Maple 8/9
Luokissa versio 8, Maplesoft on julkistanut version 9, milloin saataneen. Tosin ei liene mitään dramaattista uutta.
1. Työskentelyohjeita, työarkin käsittelyn perusasiat
Muista tallettaa aika ajoin/save your work often (CTR-S)
. Maple näyttää luokissa silloin tällöin kaatuvan (ainakin ennen, toivottavasti ei enää).
Talletus on joka tapauksessa syytä tehdä aina ennen jotain potentiaalisesti isoa laskentaa. Muista lyhyt:
CTR-S
Tämä työarkki sisältää ohjeita ja ohjeisiin liittyviä tehtäviä, joita voi samantien
ryhtyä kokeilemaan. Voit tehdä muistiinpanoja työarkille ja tallettaa sen itsellesi.
Suositus: Selaa työarkkia jonkin matkaa, totuttele heti helpin käyttöön.
Harjoitustehtävädokumentti:
Kannattaa aloittaa INSERT-valikon SECTION-valinnalla ja napsauttaa muutama sektio heti kättelyssä arkille.
Huomaa, että työarkin voi tallettaa myös HTML-muotoon. Tosin harjoitusratkaisuja esiteltäessä Maple ws-muoto
on yleensä parempi, mutta myöhempää katselua varten taas htlm-doku on tosi hyvä juttu.
Elämänohje:
Maplen filosifiaa kannattaa opetella senverran, että työskentely käy nautittavaksi.
Goals for this exercise:
-
Työarkin käsittely/Handling of worksheet
-
Peruslaskutoimitukset ja sievennykset/Basic arithmetic and simplifications
-
Grafiikka/Graphics
-
Vapaat ja sidotut muuttujat/Free and bound variables
-
Lauseke vs. funktio / Expression vs. function
-
Matriisit ja vertailu Matlab-työskentelyyn/ Matrices and comparison to Matlab work
-
Perustietorakenteet, erit.
jonot, joukot, listat. /
Basic data types
,
especially
sequences, sets, lists
Kannattaa harjoitella myös teknisiä asioita, kuten työarkin printtaamista ym.
Katsotaan ensin työarkkiin (worksheet) liittyviä asioita.
-
Uuden (laskenta)kehotteen saa hiirellä työkalunauhasta [
>
] tai CTR-J (jälkeen) tai CTR-K (ennen)
-
Laskentakehote->tekstitila:
T (
left to the previous one
)
-
Matemaattinen teksti ja tekstimuotojen muunnokset: Maalaa hiiren vasemmalla, klikkaa oikeaa, saat valikon.
-
Uusi luku: INSERT-valikko, ->SECTION
-
Leikkaa/liimaa: UNIX/X:ssä oikein kätevä, eli kuten aina X:ssä
-
- Maalataan hiiren vasemmalla
-
- viedään kursori haluttuun kohtaan
-
- liimataan keskimmäisellä
-
(Windows:ssa maalaus, CTR-C, vienti, CTR-V)
-
Ongelmia: Joskus cut/paste ei toimi Maplen ja komentoikkunan yms. välillä, joskus taas toimii.
-
(Eri Maple-ikkunoiden kesken toimii aina.)
-
Kursori voi joskus kadota kesken kaiken, ikkunan minimoiminen ja palautus voi auttaa, tai sitten ei.
-
Jos työarkin selaus käy hitaaksi ja usein muutenkin, kannattaa valita EDIT-valikosta
remove output .
Se on kätevä myös työarkin pakkaamiseen, turha säilytellä isoja kuvia ym. kun ne on talletettuna koodiin.
-
Käänteinen toimenpide on EDIT-valikon edellinen valinta:
execute worksheet.
Maple as a Math textprocessing system:
Convenenient for student project type of work. Result is not of very high quality.
Recommendation: Use LaTeX for serious work. Maple is a convenient tool for generating LaTeX-formulas.
Also, the export->HTML makes an html-document, which is not too large, and is easy to further edit, if needed.
The formulas and figures are gif-images, Maple has also MathML-support (but I have no experience on it.)
Nätti esimerkki Maplella generoidusta ja jälkeenpäin editoimalla parannellusta html-dokusta on
Virrankosken
Maple-opas.
For more details with illustrations see ...
maple
/
gsg.pdf
Työarkin painikkeita ja käsittelyä on selostettu havainnollisin kuvin .
../maple/gsg.pdf:
ssä.
Esim. paletit (insert-valikosta), smartplotit, ym. "modernit" käyttömukavuudet selitetään gsg:ssä tarkasti.
2. Viitteitä, työarkkeja, koodeja
Samat linki ovat luentosivulla.
[HAM] Apiola: Symb ja num. lask Maple-ohjelmalla, Otatieto 588
Tämä teos ilmeisine puutteineenkin lienee hyödyllinen. Perustuu versioon 5.
Täydennystä vaatii erityisesti matriisilaskentaosuus, sillä uusi LinearAlgebra-tyyli tuli vasta versioon 6.
Kirjastossa useita, jos haluat omaksi, saat minulta alennushintaan (10 e).
Kurssin Maple-hakemisto
: www.math.hut.fi/teaching/numsym/04/maple/
gsg.pdf, lrnguide.pdf, prguide.pdf (Getting Started, Learning, Programming, Maple 7)
Näitä on myös laitoskirjastossa manuaalihyllyssä ainakin kahdet kappaleet.
-
[VIR] Virrankoski: http://www.matta... <----- Simon Matta-referenssi
[PIKA] Apiola-Peltola: Maple-pikaopas http://www.math.hut.fi/teaching/k3/maple-pikaopas.html
[SOL] Solmun Maple-kirjoitus http://www.math.helsinki.fi/Solmu/solmu12/apiola
[HECK] Heck: An Introductio to Maple (Springer), täydellisin ja kattavin Maple-kirja
[ISR] Israel: Calculus with Maple (pari ylim. kappaletta kirjastossa)
Israel: Maple advisor database (kts. linkki luentosivulla)
[Coomb] Coombes-Hunt-Lipsman-Osborn-Stuck: Diff. Equations with Maple (ainakin 1 kirjastossa)
Kurssia varten kirjoitettuja/tettavia Maple-työarkkeja, kuten LA, ominaisarvot, lindys, fourier, numint, ...
maple/numsym04.mpl
3. Opiskelusuositus
Käy samalla läpi [HAM]-kirjan ss. 13 - 51 (Alkutoimenpiteet)
4. Työarkin (worksheet) lataaminen
-
Kun lataat työarkin FILE-valikon OPEN-valinnalla, saat käyttöösi visuaalisen esityksen Maple-työstä.
-
Työarkilla olevat
komennot suorittuvat vasta,
kun siirryt punaiseen INPUT-soluun ja
painat ENTER:
iä.
Koko työarkin kaikki komennot saat suoritetuksi
Edit valikon
valinnalla "
execute worksheet
", kuten edellä todettiin.
Jos haluat jatkaa kokeiluja tällä kohdalla, tee lisää kehotteita joko klikkaamalla kohtaa >
tai CTR-J (jos jälkeen) (CTR-K (ennen))
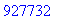
5. Laskentoa numeroilla
Laskuoperaatiot ovat "normaalit"
+-*/^
,
kertomerkkiä ei saa jättää
pois (kuten Mathematicassa)
Kokeile jotain, voit myös sijoittaa muuttujiin tyyliin:
| > |
oso:=123; nimi:=-456; luku:=oso/nimi;
|
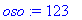
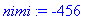
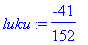
Maple vaatii loppumerkin, joko
;
tai
:
Kokeile, jos et jo tiedä.
Lue lisää:
-
[PIKA] s 1.3 s. 6
-
[SOL] s. 8
-
[HAM] s. 21
6. Laskentoa symboleilla ja numeroilla
Pohdiskelua
Lue
-
[SOL] s 15-16 Symbolien hallintaa ja periaatteita
-
[HAM] s. 70 - 71 (korjaus:
http://www.math.hut.fi/~apiola/maple/opas/eval.html
)
(see Heck Ch 3 Variables and names p. 65 -..
The secret behind success of CA :
free (unbound) variables
. )
On hyvä totutella laittamaan
restart
työarkin alkuun (ja muihinkin hengähdyspaikkoihin)
Painele nyt ENTER:iä ja palaa ohjeen mukaan takaisin.
| > |
lauseke:=(a+b)^2; # Muuttujat a ja b ovat "vapaat"
|
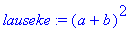
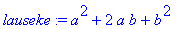
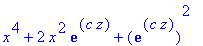
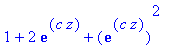
Tämä on ensimmäinen merkittävä havainto: Kun x muuttuu, niin
lauseke
muuttuu, koska yllä olevassa sijoituslauseessa muuttujat a ja b olivat vapaat.
Warning, premature end of input
Jos haluat vapauttaa vain joitakin valittuja muuttujia, niin:
Muuttujien vapauttaminen arvostaan:
Joko
a:='a';
tai
unassign('a'):
| > |
a:='a': # Vapautetaan a
|
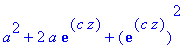
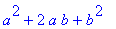
Tässä on ensimmäinen ja tärkeä syy symbolilaskennan onnistumiselle.
Vakiot Pi ja I
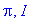
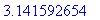
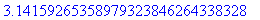
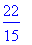
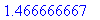
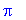
Huomaa tämä
: Maple osaa vain "tekstinkäsitellä"
pi
:tä, laskentaan tarvitaan
Pi
Tässä tulee usein virheitä alkavalle Maple-urheilijalle.
-
Virhetilanteista yleensä:
-
[HAM] Liite A s. 191 -198,
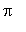 -problematiikka s. 192
-problematiikka s. 192
-
[PIKA] Lopussa lyhyt lista (jossa myös samainen
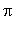 )
)
Kompleksilukuja, imag. yksikkö
I
Kompleksisievennys
, erityisesti
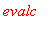
Warning, premature end of input
| > |
(1+2*I)/(2-3*I); # Numeerinen kompleksiluku muuntuu automaattisesti muotoon x+I*y .
|
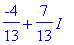
Jos kompleksiluku annetaan symbolisessa muodossa, Maple olettaa
a
:n ja
b
:n reaalisiksi esityksessä
a+I*b
.
Error, missing operator or `;`
| > |
z1:=a1+I*a2;z2:=a2+I*b2;
|
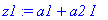
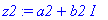
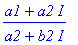
Komento
evalc
on varsin tehokas, kannattaa muistaa kompleksisievennyksissä.
Warning, premature end of input
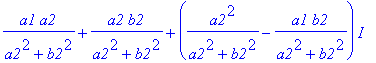
.
Error, missing operator or `;`
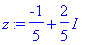
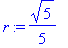


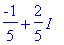
evalc
did a good job again.
Example:
complex roots
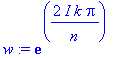
| > |
with(plots): # load the plots-package
|
Warning, the name changecoords has been redefined
| > |
setoptions(scaling=constrained,axes=framed): # Sama skaala akseleilla
|
| > |
n:=5: ykkosen5juuret:=seq(w,k=0..n-1);
|
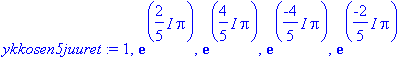
| > |
rinkulat:=complexplot([ykkosen5juuret],style=point,symbol=circle,symbolsize=15):
|
| > |
yksikkoymp:=complexplot(exp(I*Pi*t),t=0..2*Pi,color=blue):
|
Grafiikat saadaan samaan kuvaan funktiolla
display
(joka asustaa
plots
-pakkauksessa), kts alempana.
| > |
display(rinkulat,yksikkoymp);
|
![[Maple Plot]](images/perusteita32.gif)
Huom:
complexplot
tuli vasta versiossa 7, siksi [HAM]:ssa esitettävät pikku konversiotemput eivät ole enää tarpeen kompleksipiirron yhteydessä.
Warning, premature end of input
Vrt: Matlab:
>> n=5;
>> K=0:n-1;
>> w=exp(2*K*i*pi/n);
>> plot(w,'or')
>> hold on
>> t=linspace(0,2*pi); plot(exp(i*t),'b')
>> axis equal
7. Komentojen "hidastusmuodot" alkavat isolla kirjaimella.
(Itse luettavaksi.)
Usein on hyvä estää lopullinen evaluointi ainakin aluksi. Joillakin funktioilla on iso-kirjainalkuinen "inert form".
Yleensä etuhipsukoita ' ' voi myös käyttää evaluoinnin estoon.
| > |
Int(x*sin(x),x); # hidastusmuoto (inert form), alkaa isolla I:llä
|
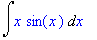
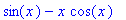
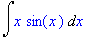
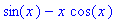
Aika kätevä tyyli (ala Heck): (Näet heti, ymmärsikö Maple sinut oikein.)
| > |
Int(x*sin(x),x); value(%);
|
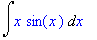
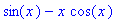
Hidastusmuoto estää evaluoinnin
, se tarjoaa kätevän tavan kirjoittaa matemaattisia kaavoja käyttämällä Maplen yhtälörakennetta.
| > |
Int(x*sin(x),x)=int(x*sin(x),x);
|
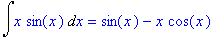
| > |
Int(x*sin(x),x): %=value(%); # Kirjoitustyötä säästävä (Heck-)tyyli.
|
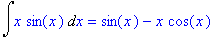
Evaluointi voidaan estää myös 'hipsukoilla'
, vrt [SOL] s. 9 rivi 1 ja s. 15. Tähänpä tuo edellä ollut muuttujan vapauttaminen arvostaankin perustuu.
| > |
'int(x*sin(x),x)'=int(x*sin(x),x);
'diff(x*sin(x),x)'=diff(x*sin(x),x);
|
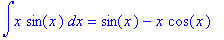
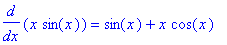
Otetaan vielä sin:n ja cos:n yhteenlaskukaavat (vaikkeivät liitykään hidastusmuotoon, mutta kylläkin tuohon yo. tyyliin. )
| > |
sin(alpha+beta): %=expand(%);
cos(alpha+beta): %=expand(%);
|
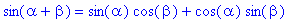
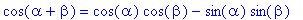
8. Defining Variables and Functions
-
Tämä on
tärkeä asia
ymmärtää kunnolla.
-
[SOLmu] s. 17 Ohjelmointi
-
[HAM] 2.4 Matemaattiset funktiot s. 60 - 63
Israel: Advisor database ..maple/advisor/fundef.mws
Pohdiskelua
Matemaattisen funktion käsittely
Maple-lausekkeena
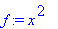
Määrittelemme muuttujan f, jota käytämme matemaattisen funktion tavoin. Maplen kannalta
f on muuttuja
, jonka arvoksi olemme sijoittaneet lausekkeen
x^2
.
Jos haluamme laskea lausekkeen arvon eri x:n arvoilla, joudumme käyttämään subs-komentoa.
Warning, premature end of input
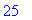
| > |
eval(f,x=5); # Näinkin voidaan, tätä tapaa käytetty gsg:ssä.
|
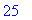
Jos haluat seurata lauseke/funktio-juonta, hyppää tässä kohdassa
seq
-kometojen yli.
Warning, premature end of input
| > |
seq(subs(x=k, f),k=0..10);
|
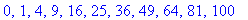
| > |
a:=-4: b:=4: N:=10: h:=(b-a)/N: arvojono:=seq(subs(x=a+k*h, f),k=0..N);
|
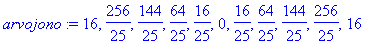
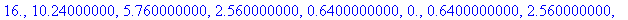
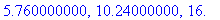
VAROITUS: Kun matemaattista funktiota käsitellään lausekkeena, on oltava johdonmukainen. Siitä ei saa välillä käyttää merkintää f(x), tietenkään!
Kokeile vaikka:
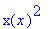
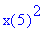
Matemaattisen funktion käsittely
Maple-funktiona:
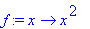
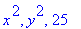
unapply
on toinen funktion määrittelytapa.
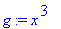
| > |
g(5); # Tämä on tuhoon tuomittu.
|
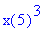
Huomaamme nyt, että olis ollut mukavampi käsitellä funktiona. No sehän käy:
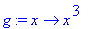
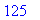
What is the difference
unapply vs ->
?
-
Nuolimäärittely evaluoi (vasta) suoritusaikana.
-
unapply evaluoi (jo) määrittelyaikana.
| > |
a:=x^2: f:=x->a;g:=unapply(a,x);
|
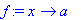
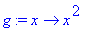
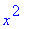
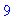
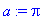
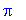
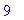
Tässä tilanteessa siis nuolimääritys
->
toimi "omituisesti", kun taas
unapply
toimi "odotetusti".
Siniset määritysrivit yllä kertovat kyllä asian hyvin, niitä kannattaa seurailla.
Error, `->` unexpected
Jatketaan tästä (harj0):
Varoitus:
Hengenvaarallista: Älä koskaan määrittele funktiota tyyliin F(x):=lauseke;
Tällöin tulee määritellyksi funktion F arvo yhdessä pisteessä x, muilla symboleilla funktio f on määrittelemätön.
Poikkeus
: Funktion määrittelyä täydentävien
poikkeusarvojen
määrittelyssä tämä on hyödyllistä, esimerkki otetaan kohta.)
Palataan nyt vielä tuohon hengenvaaraan:
| > |
F(x):=x^3; # kokeillaan kiellettyä leikkiä.
|
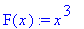
Tuo on syntaksiltaan oikein, mutta hyvin hämäävää.
Mitä on F(x)
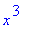
Näyttää, kuin toimisi oikein. Vaan eipas toimi muilla kuin x:llä.
| > |
F(x),F(3),F(a),F(sin(z));
|
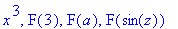
Toisin sanoen funktio on määritelty vain, kun argumenttina on symboli
x
.
Warning, premature end of input
Esimerkki:
Funktion määrittelyn täydentäminen poikkeusarvoilla
.
Haluamme määritellä funktion, jota joskus kutsutaan nimellä
sinc,
olkoon tässä vain F
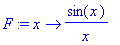
Error, (in F) numeric exception: division by zero
Yleinen sääntö ei määrittele F-funktiota 0:ssa, koska siinä tulee 0:lla jako.
Annamme siksi funktiolle 0:ssa sopivan arvon suoralla asetuksella:
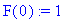
| > |
F(a),F(1/2),F(0),F(sin(x));
|
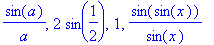
| > |
seq(F(x),x=-2..2);evalf(%);
|
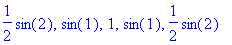
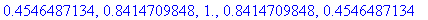
Remember:
evalf
means:
eval
uate
f
loating point.
Warning, premature end of input
-
Lue lisää:
-
[HAM] ss. 62-63
Jatketaan aihetta:
Newtonin menetelmän
valossa
.
(Voi olla hyvä lukea ensin derivaatoista, vaikka Virrankosken oppaasta tai HAM:sta, ehkä kannattaa tehdä ensin alla oleva pikku tehtävä.)
Olkoonpa ratkaistavana yhtälö
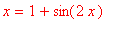 .
.
Määritellään funktio:
Warning, premature end of input
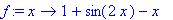
| > |
N1:=x->x-f(x)/diff(f(x),x);
|
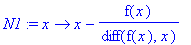
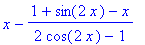
Ihan hyvä, mutta tässä tyylissä tehdään paljon työtä, jokaisella kutsulla muodostetaan ensin f-funktion symbolinen
derivaatta. Huomattavasti ekonomisempaa on tehdä symboliset operaatiot vain kerran, määrittelyaikana:
| > |
N:=evalf@unapply(x-f(x)/diff(f(x),x),x);
|
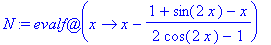
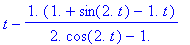
| > |
for j from 1 to 5 do
x[j]:=N(x[j-1]):
end do:
|
| > |
seq(eval(x[j]),j=0..5);
|
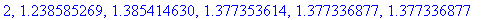
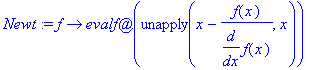
Jos haluaisimme määritellä yleisen "kirjastofunktion"
Newt
, voisimme tehdä funktion, joka ottaa syötteeksi funktion f ja palauttaa tulokseksi iterointifunktion
Newt:
| > |
Newt:=f->evalf@unapply(x-f(x)/diff(f(x),x),x);
|
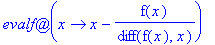
Esim
.
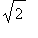 , eli funktion
, eli funktion
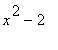 nollakohta.
nollakohta.
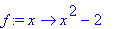
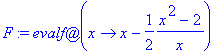
Voimme iteroida ilman for-do-rakennetta @@-operaattorilla:
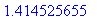
Iterointioperaattori @@ (kts. [HAM] s. 64)
| > |
(F@F@F@F@F)(10.); # Sama asia pitemmin.
|
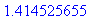
Lue iterointia koskevia varoituksen sanoja s. 66 [HAM].
Harjoitustehtävä
Määrittele polynomifunktio
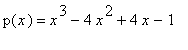 .
.
Määritä nollakohdat ja paikalliset minimit sekä maksimit. Piirrä funktio ja sen derivaatta.
Tarkista laskemalla funktion arvot, että nollakohdat ovat nollakohtia.
Käsittele polynomia ensin lausekkeena ja sitten funktiona. Mitkä ovat kunkin tavan hyvät/huonot puolet.
Derivaattalauseke -- diff
Derivaattafunktio -- D (Käyttele helppiä )
?plot, ?solve,?fsolve ?diff, ?D
Tämäntyyppisten tehtävien, niin yksinkertaisia matemaattisesti kuin ovatkin, sujuva hallinta tekee Maple-työskentelystä nautittavaa puuhaa ja auttaa pitkälle.
9. Sievennystä ja yhtälön ratkaisua
Pohdiskelua
simplify
- yleissieventäjä, ensimmäiseksi tarjoiltava.
expand
- kertoo auki
collect - kokoaa
? collect
ja kokeile joitakin esimerkkejä. Varsin hyvä komento monessa paikassa.
factor
- Jakaa tekijöihin.
convert
- ... Monenmoisiin konversioihin sievennyksessä esim
convert(lauseke,parfrac,muuttuja);
Huomaa, että lauseke ei muutu, uusi tulos palautetaan. Jos halutaan päivittää lauseke, on komennetava
lauseke:=convert(lauseke,parfrac,muuttuja);
solve
- ratkaisee yhtäön tai systeemin
fsolve
- ratkaisee numeerisesti
| > |
(x^3+1)/(x^2-x+1);simplify(%);
|
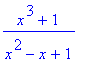
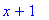
| > |
expand((x^2-4)*(x+1)*(x-2)*(x^2+x+1));
|
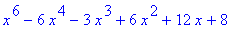
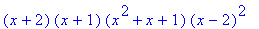
Yhtälöistä
-
[SOL] s. 11-12
-
[HAM] s. Luku 6 s. 133 - 142
| > |
yhtalot:={2*x-5*y=12, 12*x+4*y=17}; # Kyseessä on joukko
|
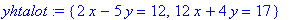
| > |
ratk:= solve(yhtalot, {x,y});
|
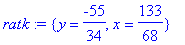
Maple ei sijoita ratkaisuja muuttujille arvoiksi, vaan palauttaa sijoitussäännöt. Ne voidaan antaa suoraan
| > |
subs
-komennolle. Mieti seuraavan komentojonon logiikkaa!
|
Warning, premature end of input
| > |
subs(ratk,x),subs(ratk,y);
|
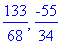
| > |
X:=subs(ratk,x); Y:=subs(ratk,y);
|
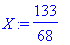
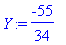
Tarkistaminen käy vaivattomasti:
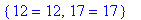
Voidaan myös käyttää
lhs
(left hand side) ja
rhs
(right hand side)-tapaa, mutta se on hiukan vähemmän elegantti ja myös altis Maplen harrastamalle järjestyksen vaihtumiselle ratkaisujoukossa. Niinpä tätä tyyliä ei voida ajaa automaattisesti, vaan tuloksiin on puututtava interaktiivisesti, mikä voi olla kiusallista, jos on "vakavahenkisestä" dokumentista kyse. Joka tapauksessa tämäkin tyyli kannattaa omaksua.
Error, missing operator or `;`
| > |
rhs(ratk[1]);lhs(ratk[1]);
|
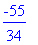
| > |
lhs(ratk[2])=rhs(ratk[2]);
|
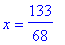
Ratkaisun sijoittaminen muuttujan arvoksi
Tässä nyt on toisin sanoin selitetty samaa, pyyhi omasta dokustasi pois tai järjestä paremmin.
Tietysti näin:
| > |
X:=rhs(ratk[1]);Y:=rhs(ratk[2]);
|
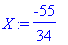
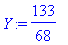
Turvallisempi ja elegantimpi tapa (jota edellä mainostettiin):
Suorita ratk-yhtälöiden ilmaisemat korvaamiset lausekkeessa (pelkkä) x ja
suorita ratk-yhtälöiden ilmaisemat korvaamiset lausekkeessa (pelkkä) y .
Edellisessä y-yhtälö jää vaille käyttöä (kun pelkkä x ei sisällä y:tä) ja jälkimmäisella vastaavasta syystä x-yhtälö.
ratk
-joukon järjestys ei näyttele mitään osaa.
Warning, premature end of input
| > |
X:=subs(ratk,x);Y:=subs(ratk,y);
|
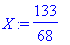
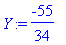
Tehokkain, mutta turvattomin tapa, joskus kylläkin tosi kätevä:
assign(ratk);
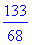
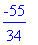
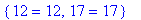
| > |
solve(yhtalot,{x,y}); # assign-komennon jälkeen x ja y eivät ole #vapaita muuttujia, josta syystä solve menee virheeseen.
|
assign(ratk);
toimii ikäänkuin ratk-yhtälöissä
yhtälömerkki (=) vaihdettaisiin sijoitusmerkkin (:=)
Yhtälöiden toteutuminen saadaan hyvin kätevästi tarkistetuksi kirjoittamalla vain
yhtalot;
Sensijaan yhtälöiden ratkaisua ei voida toistaa,
ennekuin muuttujat x ja y on vapautettu arvoistaan.
| > |
x:='x':y:='y':solve(yhtalot,{x,y});
|
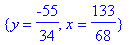
Joukot { }, jonot, listat [ ]
Tässä vähän University of North Carolinan sivulta poimittua tekstiä:
Observe that we have now employed three different kinds of grouping symbols: "()","{}", and "[]". They are used for different purposes, and Maple requires that they be used correctly. The standard parentheses "()" are used with functions as in
factor(x^2-1)
and
sin(Pi)
. The braces "
{}
" are used to group a set as in
{x,y}
. The square brackets "
[]
" are used to pick a coordinate from a group as in
sol[2]
. We will see other uses for these symbols.
Hakasulut ovat myös listasulut.
Tärkeimmät tietorakenteet:
-
Jono
, esim:
-
> jono:=a,b,c;
-
Lista,
esim:
> lista:=[a,b,c];
> op(lista); # Listan operandi on sisältönä oleva jono
-
Joukko
, esim:
> joukko:={a,b,c};
> op(joukko); # Vastaavasti joukon operandi
Huom
: Listan järjestys on käyttäjän hallinnassa, joukon ei.
Joukon hyöty on ainakin se, että Maple osaa poistaa toistot ja joukko-operaatiot toimivat.
map
- funktion soveltaminen listan (tai muun rakenteen) jokaiseen alkioon (osaan)
Error, missing operator or `;`
| > |
lista:=[a,b,c];map(f,lista);
|
![lista := [a, b, c]](images/perusteita112.gif)
![[a^2-2, b^2-2, c^2-2]](images/perusteita113.gif)
| > |
jono:=a,b,c;lista:=[a,b,c];op(lista);joukko:={a,b,c}; op(joukko);
|
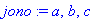
![lista := [a, b, c]](images/perusteita115.gif)
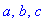
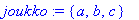
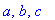
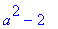
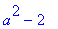
Huomaa, että jono ei ole samanlainen "paketti" kuin lista tai joukko. map-esimerkki osoittaa, että voidaksemme soveltaa tällaista operaatiota jonoon, se on ensin ympäröitävä listasuluilla
[]
ja lopuksi riisuttava sulut pois tuloksesta
op
-komennolla:
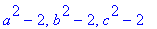
10. Piirtoa
[SOL] ss. 10 - 11
[HAM] Luku 3 ss. 89 - 100
Tavallinen käyrien piirto
Käyräparven voi sulkea joko joukkosulkuihin
{ }
tai listasulkuihin
[ ]
.
Jälkimmäinen lienee suositeltavaa, koska järjestys on silloin käyttäjän hallinnassa (esim jos halutaan värit hallitusti, tms).
| > |
plot([sin(x),cos(x)],x=0..4*Pi);
|
![[Maple Plot]](images/perusteita122.gif)
-
Ota hiiren vasemmalla kiinni kuvasta, saat kehyksen ja uudet valikot.
Valitse sama mittakaava akseleilla (1:1)
-
Jos grafiikka alkaa hidastaa työarkin selausta, kannattaa valita EDIT-valikon alimmasta,
Remove output.
Sitä kannattaa käyttää muutenkin silloin tällöin. Työarkki tiivistyy (ja nopeutuu) kummasti. Outputit saa takaisin saman EDIT-valikon toiseksi alimmaisesta
execute worksheet
-
Huomaa: Pi on Iso P, pieni i . (pi kirjoittuu oikean näköisesti, mutta Maple ei tunnista sitä
muuksi kuin kreikkalaiseksi kirjaimeksi. ) [No johan tuosta huomauteltiin.]
Parametrimuotoinen piirto
Syntaksi poikkeaa aika vähän, tämä täytyy vain oppia (tai katsoa aina uudelleen helpistä).
Aina ei ole hauskaa joutua valitsemaan hirellä, samaskaalaiisuus (ja monia muita) voidaan antaa plot-komennon tarkentimena.
| > |
plot([cos(t),sin(t),t=0..2*Pi],scaling=constrained);
|
![[Maple Plot]](images/perusteita123.gif)
Pisteet voidaan yhtä hyvin ajatella kompleksitason pisteinä. complexplot osaa käsitellä suoraan reaalimuuttujan kompleksiarvoista funktiota. Tässä on sekin mukava piirre, että syntaksi on luonnollisempi ja siten helpompi muistaa kuin tuossa parametrimuotoisessa R^2-piirrossa.
Warning, the name changecoords has been redefined
| > |
complexplot(cos(t)+I*sin(t),t=0..2*Pi,scaling=constrained,color=blue);
|
![[Maple Plot]](images/perusteita124.gif)
Edellinen voidaan ilmaista lyhyemmin eksponenttifunktion (Eulerin kaavan) avulla. Piirretään vaihteeksi pelkät pisteet.
| > |
complexplot(exp(I*t),t=0..2*Pi,scaling=constrained,color=cyan,style=point);
|
![[Maple Plot]](images/perusteita125.gif)
Taulukoidun datan piirto ("listaplotti")
Sometimes we will be interested in functions defined in terms of a discrete
table of values rather than a formula. For example, consider the following table of
temperatures recorded at various times on a spring day in Raleigh.
Time: | 6:00 a.m. | 10:00 a.m. | 12:00 p.m. | 4:00 p.m. | 5:00 p.m.
----------------------------------------------
Temp: | 45 deg. | 57 deg. | 65 deg. | 67 deg. | 66 deg.
Table of Temperatures on a Spring Day in Degrees Fahrenheit
To plot this data you must first define the points as a list. Since the time is recorded in a cyclic fashion, we will plot the times in the so-called "military style", i.e. 6:00 a.m. is 0600 and 6:00 p.m. is 1800.
| > |
ListOfPoints := [[600,45], [1000,57], [1200,65], [1600,67], [1700,66]];
|
![ListOfPoints := [[600, 45], [1000, 57], [1200, 65], [1600, 67], [1700, 66]]](images/perusteita126.gif)
The
plot
command allows you to plot a list of points and to connect them with straight lines (unless you choose another option). This is illustrated in the next command. Notice also the option which produces a title on the plot.
| > |
plot(ListOfPoints, title="Temperatures at Various Times");
|
![[Maple Plot]](images/perusteita127.gif)
While the data can be plotted in this way, because the data is given for a discrete set of points you may prefer the
style=POINT
option as illustrated in the next command. Note also the effect of the
symbol=CIRCLE
option.
| > |
plot(ListOfPoints, style=POINT, symbol=CIRCLE,symbolsize=15, title=`Temperatures at Various Times`);
|
![[Maple Plot]](images/perusteita128.gif)
Exercise
1. Plot the graph of
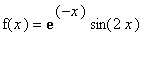 over the interval [
over the interval [
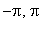 ] .
] .
2. Make a plot of the points in the following table:
X: | -1 | 0 | 1 | 2 | 3
-------------------------------------------
Y: | 2.72 | 1 | 0.368 | 0.135 | 0.0498
Make two plots, one with the points connected and the other with only the data points.
Miten saadaan kätevästi koordinaattiparien lista [[x1,y1],[x2,t2],...] ?
Olkoon annettu numeeriset listat (Matlabissa sanoisimme vektorit) X ja Y. Matlabin plot toimii tyyliin plot(x,y);
Maplessa täytyy muodostaa parien lista vaikkapa tähän tapaan:
| > |
a:=-Pi:b:=Pi:N:=20:h:=(b-a)/N:x:=seq(evalf(a+i*h),i=0..N);
|
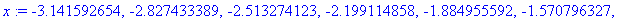
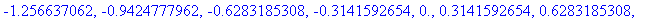
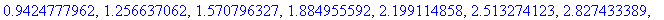
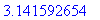
Olkoot y-arvot vaikkapa sin-funktion arvoja x-pisteissä. Parijono saataisiin nyt näin:
| > |
xy:=[seq([x[i],sin(x[i])],i=1..N+1)];
|
![xy := [[-3.141592654, .4102067615e-9], [-2.827433389, -.3090169936], [-2.513274123, -.5877852522], [-2.199114858, -.8090169941], [-1.884955592, -.9510565163], [-1.570796327, -1.], [-1.256637062, -.9510...](images/perusteita135.gif)
![xy := [[-3.141592654, .4102067615e-9], [-2.827433389, -.3090169936], [-2.513274123, -.5877852522], [-2.199114858, -.8090169941], [-1.884955592, -.9510565163], [-1.570796327, -1.], [-1.256637062, -.9510...](images/perusteita136.gif)
![xy := [[-3.141592654, .4102067615e-9], [-2.827433389, -.3090169936], [-2.513274123, -.5877852522], [-2.199114858, -.8090169941], [-1.884955592, -.9510565163], [-1.570796327, -1.], [-1.256637062, -.9510...](images/perusteita137.gif)
![xy := [[-3.141592654, .4102067615e-9], [-2.827433389, -.3090169936], [-2.513274123, -.5877852522], [-2.199114858, -.8090169941], [-1.884955592, -.9510565163], [-1.570796327, -1.], [-1.256637062, -.9510...](images/perusteita138.gif)
![xy := [[-3.141592654, .4102067615e-9], [-2.827433389, -.3090169936], [-2.513274123, -.5877852522], [-2.199114858, -.8090169941], [-1.884955592, -.9510565163], [-1.570796327, -1.], [-1.256637062, -.9510...](images/perusteita139.gif)
![xy := [[-3.141592654, .4102067615e-9], [-2.827433389, -.3090169936], [-2.513274123, -.5877852522], [-2.199114858, -.8090169941], [-1.884955592, -.9510565163], [-1.570796327, -1.], [-1.256637062, -.9510...](images/perusteita140.gif)
![xy := [[-3.141592654, .4102067615e-9], [-2.827433389, -.3090169936], [-2.513274123, -.5877852522], [-2.199114858, -.8090169941], [-1.884955592, -.9510565163], [-1.570796327, -1.], [-1.256637062, -.9510...](images/perusteita141.gif)
![xy := [[-3.141592654, .4102067615e-9], [-2.827433389, -.3090169936], [-2.513274123, -.5877852522], [-2.199114858, -.8090169941], [-1.884955592, -.9510565163], [-1.570796327, -1.], [-1.256637062, -.9510...](images/perusteita142.gif)
| > |
plot(xy);plot(xy,style=point,symbol=circle);
|
![[Maple Plot]](images/perusteita143.gif)
![[Maple Plot]](images/perusteita144.gif)
Huom:
plots
-pakkauksessa on
listplot
ja
pointplot
. Maplelle luonteenomaista on, että siinä on joukko redundantteja funktioita. Mielestäni on parempi oppia käyttämään harvempaa ydinfunktiojoukkoa kuin omaksua monenlaisia synonyymejä. Niissä voi toki olla joitakin uusia mahdollisuuksia, mutta esim. näissä ei välttämättä ole (kuka noita kaikkia tuhansia ehtii penkoa).
Taulukointi
Tässä teimme itse asiassa taulukon, joka on havainnollisempi usein matriisina.
| > |
txy:matrix(xy):linalg[transpose](xy):
|
Tilan säästämiseksi otetaan vähemmän dataa esimerkkiimme. Jätetäänpä myös
evalf
pois.
| > |
a:=-Pi:b:=Pi:N:=8:h:=(b-a)/N:x:=seq(a+i*h,i=0..N);
xy:=[seq([x[i],sin(x[i])],i=1..N+1)];
matrix(xy);
|
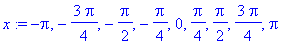
![xy := [[-Pi, 0], [-3/4*Pi, -1/2*2^(1/2)], [-1/2*Pi, -1], [-1/4*Pi, -1/2*2^(1/2)], [0, 0], [1/4*Pi, 1/2*2^(1/2)], [1/2*Pi, 1], [3/4*Pi, 1/2*2^(1/2)], [Pi, 0]]](images/perusteita146.gif)
![matrix([[-Pi, 0], [-3/4*Pi, -1/2*2^(1/2)], [-1/2*Pi, -1], [-1/4*Pi, -1/2*2^(1/2)], [0, 0], [1/4*Pi, 1/2*2^(1/2)], [1/2*Pi, 1], [3/4*Pi, 1/2*2^(1/2)], [Pi, 0]])](images/perusteita147.gif)
![matrix([[-Pi, -3/4*Pi, -1/2*Pi, -1/4*Pi, 0, 1/4*Pi, 1/2*Pi, 3/4*Pi, Pi], [0, -1/2*2^(1/2), -1, -1/2*2^(1/2), 0, 1/2*2^(1/2), 1, 1/2*2^(1/2), 0]])](images/perusteita148.gif)
| > |
array(xy); # Taas synonyymi, mutta tiettyjä erojakin yleisyydessa / matriisilaskukyvyissä.
|
![matrix([[-Pi, 0], [-3/4*Pi, -1/2*2^(1/2)], [-1/2*Pi, -1], [-1/4*Pi, -1/2*2^(1/2)], [0, 0], [1/4*Pi, 1/2*2^(1/2)], [1/2*Pi, 1], [3/4*Pi, 1/2*2^(1/2)], [Pi, 0]])](images/perusteita149.gif)
Grafiikoiden yhdistäminen, plots[display] ja textplot
Tässä tarvitaan lisägrafiikkapakkaus
plots
Warning, the name changecoords has been redefined
Selvitä itsellesi, mitä seuraavassa tehdään. Mieti tarkkaan, miksi jossain pitää antaa plot:lle argumentiksi
f(x) ja miksi taas jossain esim. tang. Voit sitten huvitella vaihtelemalla funktion määritelmää
ja / tai pistettä x0. Kirjoitetaan pieni malliskripti, jonkalaisia voit tehdä moninaisissa yhteyksissä.
| > |
x0:=1: f:=x->x^3: # Vaihtuva syöte
|
| > |
df:=diff(f(x),x): kk:=subs(x=1,df);
|
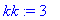
| > |
x0:=1: tang:=f(x0)+kk*(x-x0);
|
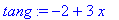
| > |
fkuva:=plot(f(x),x=0..2,color=red): tangkuva:=plot(tang,x=0..2,color=blue): p0kuva:=plot([[x0,f(x0)]],style=point,symbol=circle,symbolsize=15,color=black):
|
| > |
display([fkuva,tangkuva,p0kuva]);
|
![[Maple Plot]](images/perusteita152.gif)
Kokeile (mutta vain kerran elämässäsi, silloinkin syvästi katuen, että olit yllytyshullu),
mitä tapahtuu, kun vaihdat (:) -> (;) vaikkapa
fkuva:=; .
.. yllä. PLOT-tietorakenne paljastuu.
- No, mene edit-valikkoon ja -> remove output, kyllä se siitä.
Sometimes it will be desirable to
print text on a plot.
The
plots
procedure
textplot
will allow this. The following commands will serve as examples of the
textplo
t and
display
routines. Make sure you notice where colons and semicolons are used in these commands.
In the next commands it is important to use colons to punctuate the first two statements. Otherwise Maple will ouput an entire page of text describing the plot structure rather than the graph. The textplot in the second command causes the text x=0.6356,y=0.5000 to be printed at the point (.6356,.5000). The statement
align=RIGHT
aligns this text to the right of the point.
| > |
f := x -> exp(-x)*sin(3*x);
plot1 := plot(f, 0..3):# tai plot1:=plot(f(x),x=0..3):
plot2 := plots[textplot]([0.6356, 0.5000, "x=.6356, y=.5000"], align=RIGHT):
plots[display]({plot1, plot2});
|
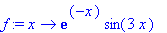
![[Maple Plot]](images/perusteita154.gif)
Huom:
plots-pakkauksen (kuten muidenkin pakkausten) funktioita voidaan käyttää myös lataamatta
koko pakkausta, tällöin pakkauksen nimeä ikäänkuin indeksoidaan ao. funktion nimellä
tyyliin
plots[display]
3d-grafiikkaa, animaatiot
Otetaan lämmönjohtumisesimerkki, jossa valaistaan
-
3d-pinnan piirtoa
-
Animaatiota
-
3d-kuvan projektiokäyräparven piirtoa
Tarkastellaan sivuiltaan lämpöeristettyä sauvaa, jonka päät upotetaan hetkellä t=0 jäävesisäiliöihin (0 astetta) ja jonka
alkulämpötilajakauma on
| > |
f:=x->100*sin(Pi*x/80);
|
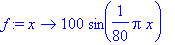
Huomaa funktiomääritys
.
Olkoon sauvan pituus L=80.
Tässä tapauksessa lämpöyhtälön ratkaisuna olevasta Fourier-sarjasta tulee vain yksi termi. Ratkaisu on (sopivalla lämmönjohtumiskertoimella)
| > |
u:=(x,t)->100*sin((Pi*x)/80)*exp(-0.001785*t);
|
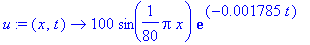
Pintapiirros
| > |
plot3d(u(x,t),x=0..80,t=0..400);
|
![[Maple Plot]](images/perusteita157.gif)
-
Klikkaa hiirellä kuvaan (ja tarvittaessa valitse "boxed") työkalunauhasta.
-
Kierrä kuvaa hiirellä.
-
Kokeile STYLE-valikosta PATCH ja PATCH with contour valintoja.
Animaatio
| > |
animate(u(x,t),x=0..80,t=0..300,frames=30,color=blue);
|
![[Maple Plot]](images/perusteita158.gif)
Lämpötilaprofiilit ja korkeuskäyrät
| > |
plot({seq(u(x,t),t=[0,10,50,100,200,300,400])},x=0..80);
|
![[Maple Plot]](images/perusteita159.gif)
| > |
contourplot(u(x,t),x=0..80,t=0..400);
|
![[Maple Plot]](images/perusteita160.gif)
Implicitplot
Tämä on periaatteessa sama kuin yhden korkeuskäyrän piirto.
| > |
implicitplot({x^2+y^2=1,x^3+y^3=1,x^10+y^10=1},x=-2..2,y=-2..2);
|
![[Maple Plot]](images/perusteita161.gif)
Tuohon tekisi mieli laittaa loppuun esim:
,color=[red,blue,black]);
mutta näköjään kaikki
plot
:n hyväksymät optiot eivät tässä toimi.
![]()
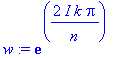
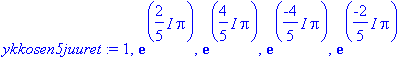
![[Maple Plot]](images/perusteita32.gif)

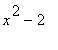 nollakohta.
nollakohta.
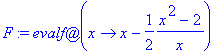
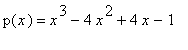 .
.
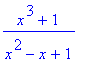
![[Maple Plot]](images/perusteita122.gif)
![[Maple Plot]](images/perusteita123.gif)
![[Maple Plot]](images/perusteita124.gif)
![[Maple Plot]](images/perusteita125.gif)
![[Maple Plot]](images/perusteita127.gif)
![[Maple Plot]](images/perusteita128.gif)
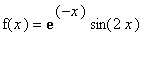 over the interval [
over the interval [
![[Maple Plot]](images/perusteita143.gif)
![[Maple Plot]](images/perusteita144.gif)
![matrix([[-Pi, 0], [-3/4*Pi, -1/2*2^(1/2)], [-1/2*Pi, -1], [-1/4*Pi, -1/2*2^(1/2)], [0, 0], [1/4*Pi, 1/2*2^(1/2)], [1/2*Pi, 1], [3/4*Pi, 1/2*2^(1/2)], [Pi, 0]])](images/perusteita147.gif)
![matrix([[-Pi, -3/4*Pi, -1/2*Pi, -1/4*Pi, 0, 1/4*Pi, 1/2*Pi, 3/4*Pi, Pi], [0, -1/2*2^(1/2), -1, -1/2*2^(1/2), 0, 1/2*2^(1/2), 1, 1/2*2^(1/2), 0]])](images/perusteita148.gif)
![matrix([[-Pi, 0], [-3/4*Pi, -1/2*2^(1/2)], [-1/2*Pi, -1], [-1/4*Pi, -1/2*2^(1/2)], [0, 0], [1/4*Pi, 1/2*2^(1/2)], [1/2*Pi, 1], [3/4*Pi, 1/2*2^(1/2)], [Pi, 0]])](images/perusteita149.gif)
![[Maple Plot]](images/perusteita152.gif)
![[Maple Plot]](images/perusteita154.gif)
![[Maple Plot]](images/perusteita157.gif)
![[Maple Plot]](images/perusteita158.gif)
![[Maple Plot]](images/perusteita159.gif)
![[Maple Plot]](images/perusteita160.gif)
![[Maple Plot]](images/perusteita161.gif)