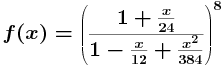- 2, 4, 6, 8, ..., 20
- 10, 8, 6, 4, 2, 0, -2, -4, ..., -10
- 1, 1/2, 1/3, 1/4, 1/5, ..., 1/10
- 0, 1/2, 2/3, 3/4, 4/5, ..., 9/10
Muista 1) Pisteittäiset laskutoimitukset, 2) Aloitus:
x=linspace(a,b,n); y=f(x); Puolipisteet komentojen lopussa
(Jos et muista, niin itket tai ainakin hiljaa kärsit.)
- exp(-x²)
- x sin(2x²+1)
- tan x välillä
[-pi/2,9*pi/2]. (Ennen axis- tai ylim-komentoa kuva on varsin epäinformatiivinen.) - Sama kuin edellä, mutta hallitummin, ilman (miltei) pystysuoria viivoja ja käyttäen hyväksi tan-funktion jaksollisuutta. Tähän voit hyvin katsoa ratkaisun suoraan C. van Loan - tiedostosta TangentPlot.m
Tämä on exp-funktion rationaaliapproksimaatio, ns. Pade-approksimaatio. Piirrä kuvaaja välillä [0,1].
Aloita vaikka: x=linspace(0,1,200);
Neuvo: Selkeyden vuoksi kannattaa ottaa käyttöön apumuuttujia, kuten osoittaja, nimittaja . Piirrä samaan kuvaan exp-funktio eri värillä ja eri kuvaan erotus f-exp.
t=linspace(0,2*pi); plot(sin(t),cos(t),'-',[1 1 -1 -1 1],[-1 1 1 -1 -1],'-'); axis([-1.5 1.5 -1.5 1.5]) axis square