Fourier-sarjat
24.11.05 KP3, L/fouriersarjat.mws ja html
| > |
with(plots):read("e:ns05.mpl");
|
Warning, the name changecoords has been redefined
Jaksollinen jatkaminen
Jokainen jollain välillä [a,b] määritelty funktio voidaan jatkaa jaksollisena (p=b-a) koko R:ään.
Esim:
| > |
f:=x->x^2: # välillä [0,1], jatka 1-jaksoisena!
|
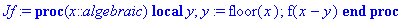
![[Maple Plot]](images/fouriersarjat2.gif)
| > |
f:=x->x^2: # välillä [-1,1], jatka 2-jaksoisena!
|
Kanttiaalto
| > |
f:=x->piecewise(x>0,1,x<0,-1); plot(f,-1..1);
|
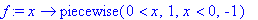
![[Maple Plot]](images/fouriersarjat4.gif)
| > |
Jf:=JJ(f,-1..1): plot(Jf,-4..4);
|
![[Maple Plot]](images/fouriersarjat5.gif)
Fourier-kertoimet, esimerkkejä Fourier-sarjoista
Fourier-kertoimien kaavat, jotka saatiin ortogonaalisuuden perusteella. Kaavat johti jo kauan ennen
Fourieria
, kukas muu kuin
Euler
v. 1777.
| > |
a0:=(1/(2*Pi))*Int(f(x),x=-Pi..Pi);
|
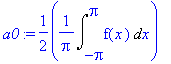
| > |
an:=(1/Pi)*Int(f(x)*cos(n*x),x=-Pi..Pi);
|
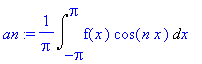
| > |
bn:=(1/Pi)*Int(f(x)*sin(n*x),x=-Pi..Pi);
|
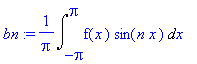
| > |
sarja:='a0'+Sum('an'*cos(n*x)+'bn'*sin(n*x),n=1..infinity);
|
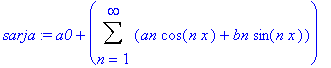
| > |
osasumma:=(x,N)->a0+add(an*cos(n*x)+bn*sin(n*x),n=1..N):
|
Fourier
-sarjojen muodostaminen on nyt helppoa. Toki voi tulla integrointivaivaa, mutta Maplea voi käyttää
nautinnollisesti hyödyksi. Voi tietysti syntyä myös tilanteita, joissa on turvauduttava numeeriseen integrointiin.
Siihenkin Maplessa on välineitä.
Esim 1, kanttiaalto
| > |
f:=x->piecewise(x>0,1,x<0,-1);
|
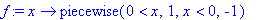
| > |
Jf:=JJ(f,-Pi..Pi); #plot(Jf,-2*Pi..2*Pi);
|
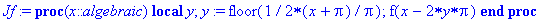
| > |
a0:=(1/(2*Pi))*Int('f'(x),x=-Pi..Pi);
|
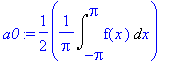
| > |
a0:=(1/(2*Pi))*2*int(f(x),x=0..Pi);
|
a0:=0;
| > |
an:=(1/Pi)*Int('f'(x)*cos(n*x),x=-Pi..Pi); an:=0;
|
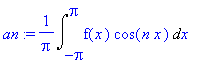
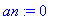
| > |
bn:=(1/Pi)*Int('f'(x)*sin(n*x),x=-Pi..Pi);
|
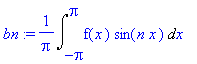
| > |
bn:=2*(1/Pi)*int(1*sin(n*x),x=0..Pi);
|
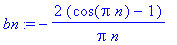
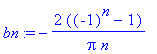
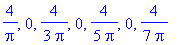
| > |
sarja:=Sum('b[n]'*sin(n*x),n=1..infinity);
|
![sarja := Sum(b[n]*sin(n*x),n = 1 .. infinity)](images/fouriersarjat21.gif)
| > |
osasumma:=(x,N)->add(bn*sin(n*x),n=1..N);
|
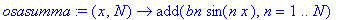
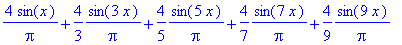
| > |
sarja:=(4/Pi)*Sum(sin(2*k-1)*x/(2*k-1),k=1..infinity); # Muista iso Sum !
|
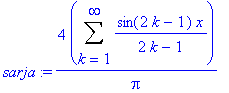
Kuvaajia:
| > |
plot([Jf(x),osasumma(x,1)],x=-2*Pi..2*Pi);
|
![[Maple Plot]](images/fouriersarjat25.gif)
| > |
plot([Jf(x),osasumma(x,1),osasumma(x,3),osasumma(x,5)],x=-2*Pi..2*Pi);
|
![[Maple Plot]](images/fouriersarjat26.gif)
| > |
plot([Jf(x),seq(osasumma(x,N),N=1..7)],x=-Pi..Pi);
|
![[Maple Plot]](images/fouriersarjat27.gif)
| > |
plot([Jf(x),seq(osasumma(x,N),N=[1,3,5,31,67])],x=-Pi..Pi,color=[gray,black,green,blue,red]);
|
![[Maple Plot]](images/fouriersarjat28.gif)
| > |
plot([Jf(x),osasumma(x,101)],x=-0.1..Pi+.1,color=[gray,blue],numpoints=100);
|
![[Maple Plot]](images/fouriersarjat29.gif)
| > |
display(%,view=[0..Pi,0.7..1.3]);
|
![[Maple Plot]](images/fouriersarjat30.gif)
Miten voi kanttiaallon F-sarja supeta, vaikka kertoimet ovat harmonisen sarjan kertoimet. sin(n*x)-termien on pakko vaikuttaa asiaan. Tutkitaan:
| > |
g:=(x,k)->sin((2*k-1)*x);
|

| > |
plot3d(g(x,k),x=-Pi..Pi,k=1..10):
|
| > |
x:=Pi/2:plot([seq([k,g(x,k)],k=1..20)]):
|
| > |
kuva:=(x,N)->plot([seq([k,g(x,k)],k=1..N)],style=line);
|
![kuva := proc (x, N) options operator, arrow; plot([seq([k, g(x,k)],k = 1 .. N)],style = line) end proc](images/fouriersarjat32.gif)
| > |
display(seq(kuva(x,150),x=[seq(0.1*k,k=0..10*3)]),insequence=true):
|
Yleinen jakso p=2L
| > |
restart: with(plots): read("e:ns05.mpl");
|
Warning, the name changecoords has been redefined
| > |
a0:=1/(2*L)*Int('f'(x),x=-L..L);
|
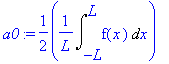
| > |
an:=1/L*Int('f'(x)*cos(n*Pi*x/L),x=-L..L);
|
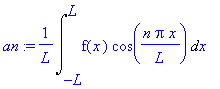
| > |
bn:=1/L*Int('f'(x)*sin(n*Pi*x/L),x=-L..L);
|
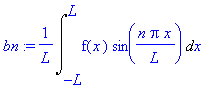
Esim: Puoliaaltotasasuunnattu siniaalto
| > |
u:= piecewise(t>-L and t < 0,0,t > 0 and t < L,E*sin(omega*t));
|
![u := PIECEWISE([0, -1/2*Pi-t < 0 and t < 0],[E*sin(2*t), -t < 0 and t-1/2*Pi < 0])](images/fouriersarjat36.gif)
| > |
L:=Pi/omega:plot(u(t),t=-1..1,axes=box); omega='omega': E:='E':L:='L':L:=Pi/omega:
|
![[Maple Plot]](images/fouriersarjat37.gif)
| > |
a0:=1/(2*L)*int(E*sin(omega*t),t=0..L);
|
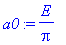
| > |
an:=1/L*int(E*sin(omega*t)*cos(n*omega*t),t=0..L); # Huom! n > 1
|
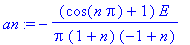
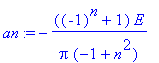
| > |
a1:=1/L*int(E*sin(omega*t)*cos(1*omega*t),t=0..L);
|
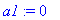
| > |
bn:=1/L*int(E*sin(omega*t)*sin(n*omega*t),t=0..L); # Huom! n > 1
|
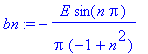
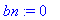
| > |
b1:=1/L*int(E*sin(omega*t)*sin(1*omega*t),t=0..L);
|
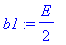
| > |
sarja:=a0+Sum(an*cos(n*omega*t),n=2..infinity)+b1*sin(omega*t);
|
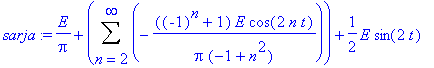
| > |
osasumma:=unapply(a0+sum(an*cos(n*omega*t),n=2..N)+b1*sin(omega*t),t,N);
|
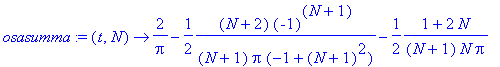
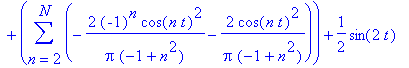
| > |
plot([u,osasumma(t,10)],t=-L..L);
|
![[Maple Plot]](images/fouriersarjat48.gif)
| > |
plot([seq(osasumma(t,N),N=2..10)],t=-L..L);
|
![[Maple Plot]](images/fouriersarjat49.gif)
| > |
plot([osasumma(t,50)],t=-L..L,numpoints=100,axes=boxed);
|
![[Maple Plot]](images/fouriersarjat50.gif)
![]()
![[Maple Plot]](images/fouriersarjat2.gif)
![]()
![[Maple Plot]](images/fouriersarjat4.gif)
![[Maple Plot]](images/fouriersarjat5.gif)
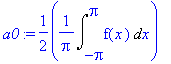
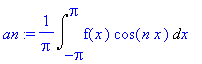
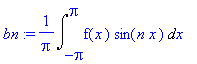
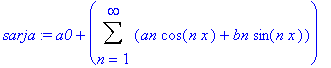
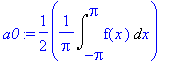
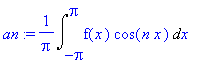
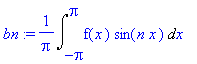
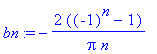
![sarja := Sum(b[n]*sin(n*x),n = 1 .. infinity)](images/fouriersarjat21.gif)
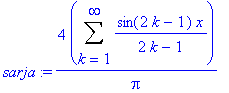
![[Maple Plot]](images/fouriersarjat25.gif)
![[Maple Plot]](images/fouriersarjat26.gif)
![[Maple Plot]](images/fouriersarjat27.gif)
![[Maple Plot]](images/fouriersarjat28.gif)
![[Maple Plot]](images/fouriersarjat29.gif)
![[Maple Plot]](images/fouriersarjat30.gif)
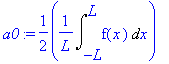
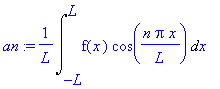
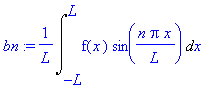
![u := PIECEWISE([0, -1/2*Pi-t < 0 and t < 0],[E*sin(2*t), -t < 0 and t-1/2*Pi < 0])](images/fouriersarjat36.gif)
![[Maple Plot]](images/fouriersarjat37.gif)
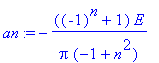
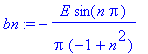
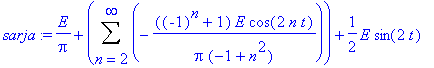
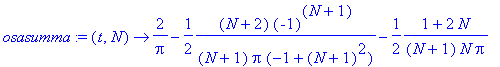
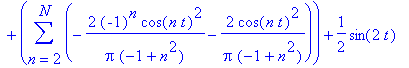
![[Maple Plot]](images/fouriersarjat48.gif)
![[Maple Plot]](images/fouriersarjat49.gif)
![[Maple Plot]](images/fouriersarjat50.gif)