Kurssista on ylimääräinen tenttimismahdollisuus lauantaina 12.5.2007 klo 10.00. Sali ilmoitetaan kyseisenä päivänä pääaulan tentti-ilmoitustaululla.

Luennoin keväällä 2007 TKK:n matematiikan laitoksella kurssin, joka johdattelee differentiaaligeometrian kauniisiin ideoihin ja tuloksiin. Erityisesti kevään 2007 kurssilla keskitytään käyrien ja pintojen geometriaan. Tavoitteena on motivoida abstraktin monistojen teorian tarvetta intuitiivisten geometristen kysymysten avulla.

Pintojen kaarevuusteoria alkoi jo Leonhard Eulerin (1707-1783) tutkimuksilla vuonna 1760 ja jatkui Jean Babtiste Marie Meusnierin (1754-1793) julkaisuilla vuodelta 1774 koskien pinnan pääkaarevuuksien ja keskikaarevuuden suhdetta: . Joseph-Louis Lagrange (1736-1813) osoitti vuonna 1760, että ehto , määrittelee luokan pintoja, jotka minimoivat annetun reunakonfiguraation sisään jäävän pinta-alan. Tällaisia pintoja kutsutaan minimipinnoiksi. Vuonna 1816 Johann Carl Friedrich Gauss (1777-1855) käynnisti modernin differentiaaligeometria kehityksen huomaamalla, että kokonaiskaarevuus voidaan laskea käyttämällä pelkästään pinnan sisäistä metriikkaa, joka on riippumaton pinnan upotuksesta ympäröivään euklidiseen avaruuteen. Tämän kuuluisan lauseen ('Theorema Egregium') julkaisuvuotta 1825 pidetään teorian lähtölaukauksena. Lisäksi Gauss selvitti kokonaiskaarevuuden roolin pinnan geodeettisen kolmion kulmien summan laskemiseksi. Tästä oli vain pieni askel yleiseen kompaktin pinnan Gauss-Bonnet-kaavaan, joka yhdistää puhtaasti topologisen pinnan invariantin, Eulerin karakteristikan ja täysin geometrisen suureen, kokonaiskaarevuuden toisiinsa:

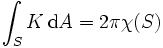
Seuraava kulmakivi oli Georg Friedrich Bernhard Riemannin (1826-1866) väitöskirja vuodelta 1854, jossa esiteltiin abstraktin lähestymistavan ideat. Tämän jälkeen teoria on laajentunut jatkuvassa vuorovaikutuksessa fysiikan ja mm. sellaisten matematiikan alojen kuin topologia, analyysi ja osittaisdifferentiaaliyhtälöiden teoria, koskettamaan lähes kaikkea modernin matematiikan ja fysiikan tutkimusta ja sovelluksia.

Kurssilla tutustutaan tähän historiallisesti ensimmäiseen vaiheeseen modernin tietämyksen valossa. Erityisesti tutustutaan Frenet-kehyksiin, kehittyviin pintoihin, minimipintoihin ja Gauss-Bonnet-lauseeseen.

Kevään 2007 kurssi on luonteeltaan yleissivistävä ja sopii kaikille matematiikasta ja sen soveltamisesta kiinnostuneille. Esitiedoiksi riittää avoin ja utelias mieli. Kurssi on mahdollista suorittaa kahdella välikokeella tai tentillä ja täydentää aktiivisella osallistumisella laskuharjoituksiin tai kurssin aihepiiriin liittyvällä harjoitustyöllä.

Tervetuloa!