
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
MATLAB-tehtäviä koskien monen muuttujan analyysia.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. Muista, että Jacobin matriisi koostuu vektori- tai skalaariarvoisen funktion F ensimmäisistä osittaisderivaatoista:
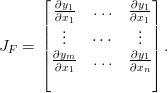
Kuinka laskisit numeerisen Jacobin matriisin? Vihje: Muista, että numeerisesti
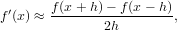
- 2. Harjoitellaan usean muuttujan funktioiden piirtämistä. MATLABissa tämä tehdään määrittelemällä ensin piirtoalueen peittävä diskretointi, tai hila. Tämä määritellään komennolla meshgrid. Luodaan esimerkiksi suorakulmion [1, 2] × [3, 4] peittävä hila:x = 1:0.2:2;
y = 3:0.2:4;
[X Y] = meshgrid(x,y);Nyt muuttujissa X ja Y ovat hilapisteiden x- ja y-koordinaatit. Niillä voidaan suorittaa laskutoimituksia kuten tavallisillakin muuttujilla; on vain pidettävä mielessä että kyseessä ovat nyt matriisit, eli yleensä haluamme valita alkioittaiset operaatiot matriisioperaatioiden sijaan.
Pintojen piirtäminen tapahtuu komennoilla surf ja mesh. Lasketaan ja piirretään funktion
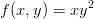
kuva:
Z = X.*Y;
% Huomaa alkoittainen kertolasku
surf(x,y,Z);.
Piirrä näillä keinoin seuraavien funktioiden kuvat
- f(x,y) =
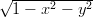 alueessa [−
alueessa [−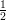 ,
,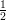 ] × [−
] × [−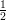 ,
,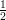 ]
]
- f(x,y) = x3 − 3xy alueessa [−1, 1] × [−1, 1].
Toinen yleinen tapa kuvata usean muuttujan funktioita on käyttää tasa-arvokäyriä. Näitä piirretään komennolla contour, syntaksi on sama kuin tavallisilla piirtokomennoilla. Kokeile piirtää myös edellisten funktioden tasa-arvokäyrät.
- f(x,y) =
- 3. Vektorianalyysissä on todistettu että funktion tasarvo-käyrä on aina gradientin normaali. Tutkitaan tätä nyt käytännössä. Piirrä funktiolle
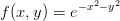
tasa-arvokäyrät haluamassasi hilassa käyttäen komentoa contour (komennon syntaksi on sama kuin tavallisten piirtokomentojen). Tämän jälkeen laske funktion numeerinen gradientti tässä hilassa funktiolla gradient. Funktio palauttaa tässä tapauksessa kaksi matriisia, joissa on pisteittäiset numeeriset estimaatit arvoille
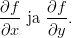
Gradientit kannattaa piirtää vektorikenttänä, MATLABin tapauksessa komennolla quiver. Esimerkiksi, jos halutut osittaisderivaatat ovat matriiseissa dx ja dy niin piirto tapahtuisi komennolla quiver(x,y,dx,dy). Lopuksi piirrä kuvat näkyviin päällekäin komentamalla:
contour(x,y,z)
hold on
quiver(x,y,dx,dy)Tutki kuvasta, ovatko gradienttinuolet suorassa kulmassa tasa-arvokäyriä vastaan.
- 4. Muista, että Jacobin matriisi koostuu vektori- tai skalaariarvoisen funktion F ensimmäisistä osittaisderivaatoista:
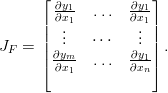
Kuinka laskisit numeerisen Jacobin matriisin? Vihje: Muista, että numeerisesti
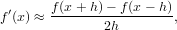
- 5. Funktiofunction Jf = numjaco(F,m,x,n)
% f is a function with m components,
% x is a vector with n components,
% the result is an m by n matrix.
Jf = ones(m,n); h = 1e-4;
f = fcnchk(F);
for j =1:n
e = zeros(n,1); e(j) = 1;
Jf(:,j) = (f(x+h*e)-f(x-h*e) )/(2*h);
end;laskee vektorikentän F numeerisen Jacobin matriisin, olettaen että käytetty kanta on standardi. Jos vektorikentässä on vain yksi komponentti, kyseessä on kyseisen funktion gradienttivektori.
Kopioi edellä oleva funktio tiedostoon, ja määrittele funktiot
- f(x,y) = x2y
- g(x,y) = xex2+y
ja laske niiden numeeriset gradientit pisteissä (1, 2) ja (2,−4). Vertaa tulosta tarkkoihin arvoihin:
![[ ] [ x2+y 2 x2+y]
∇f = 2xy ∇g = e + 2x e
x2 xex2+y](matlabHarVektori12x.png)
- 6. Piirrä funktion f(x,y) = e−x2−y2 määrittelemä pinta (x,y)-tason neliön [−2, 2] × [−2, 2] alueella. Laske tämän funktion integraali yli kyseisen neliön. Kyseisen integraalin arvo koko tason ylitse on π. Vihje: Pinnan piirtämiseen tarvitset sopivan alueen peittävän hilapisteistön. Näitä luodaan MATLABissa komennolla meshgrid, katso help meshgrid. Pinta piirretään komennolla mesh tai surf, katso dokumentaatiota.
Integraalin laskemiseen kannattaa käyttää funktiota dblquad. Katso kutsumisohjeet dokumentaatiosta. dblquadin ensimmäisen argumentin tulee olla funktio: tässä kannattaa käyttää MATLABin anonyymifunktioita. Esimerkiksi ∫ 03 ∫ 23xydxdy = dblquad(@(x,y)x.*y,2,3,0,1). Jälleen kerran, tutki dokumentaatiota function_handle.
- 7. Laske funktion f(x,y) = 3 + cos(x) + cos(y) määräämän pinnan ja suorakulmion [0,π] × [0, 2π] väliin jäävä tilavuus. Piirrä havainnolistava kuva. Vihje: Tilavuuteen tarvitset kaksinkertaista integraalia dblquad, pinta piirretään komennoilla meshgrid ja mesh.
- 8. Piirrä funktion f(x,y) = y2 −x2 tasa-arvokäyrät ja gradienttivektorikenttä, ja totea, että gradientti on aina kohtisuorassa tasa-arvokäyrää vasten. Vihje: Laske gradientti funktiolla gradient, ja piirrä tasa-arvokäyrät komennolla contour. Gradienttivektorikentän saat piirrettyä komennolla quiver.
- 9. Määritä pinnan z = −x2 − y2 normaalivektori, ja piirrä sen vektorikenttä samaan kuvaan pinnan kanssa. Vihje: Aloita määrittelemällä jokin tason suorakulmio funtion meshgrid avulla - tämän jälkeen voit määritellä pinnan, eli matriisin z. Pinnan normaalivektorin saat laskettua funktiolla surfnorm. Piirrä ensiksi pinta komennolla surf(x,y,z), sen jälkee kirjoita hold on, jonka jälkeen kirjota quiver3(x,y,z,u,v,w), missä u,v ja w ovat surfnormin palauttamat matriisit.
