
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
MATLAB-tehtäviä kompleksiluvuista ja kompleksianalyysista
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mlK001.tex
Ensiapuohjeita
- Sijoitus muuttujaan esim: >> z=(1+i)/(1-2*i)
Puolipiste lopussa estää tulostuksen. - Muuttujan sisällön näet kirjoittamalla sen nimen ilman puolipistettä
- Lopeta puolipisteeseen, jos komentosi tuottaa dataa paljon, isojen tulosteiden vilistäminen ruudulla on pelkkää kärsimystä.
- Jos kuitenkin unohdit, niin CTR-C
- Vektorin voi muodostaa esim. näin: >> vektori=[-1,0,4,5.2-3.45*i]
Pitempiin vektoreihin: help colon, help linspace - Kun teet aritmetiikkaa vektoreille tyyliin
>> x=linspace(0,1); y=(x.^2).*sin(x);
niin muista piste ja ymmärrä. (Tässä sulut vain selvennykseksi.) - Kaikki vähänkin vakavampi työskentely kannattaa tehdä avaamalla editorilla tekstitiedosto, jonne kerätään Matlab-ajon komennot (ja mahdollisesti tärkeimmät tulosteet).
- Matriisi muodostetaan tyyliin >> A=[1 2 3;4 5 6]
2. rivi: A(2,:), 3. sarake: A(:,3) . Kokeile ihmeessä!
Tämä ei siis ole tehtävä, alla vain tämän ohjeen Latex-koodi.
- Sijoitus muuttujaan esim: >> z=(1+i)/(1-2*i)
- 2. mlK002.tex
Sijoita muuttujalle z arvo 2 + 3i. Laske Matlabilla z:n reaaliosa, imaginaariosa,liittoluku, moduli (itseisarvo) ja argumentti (napakulma). Piirrä pisteet z ja z. Anna sopiva axis-komento, jotta saat paremman koordinaatiston. Piirrä sitten samaan kuvaan jana origosta pisteeseen z punaisella värillä ja origosta pisteeseen z sinisellä.
Sopivia Matlab-komentoja: real, imag, conj, abs, angle, sign, plot, axis, hold on Tutki kutakin helpillä tyyliin help real jne.
Opiskele aihetta ”kompleksilukujen piirtäminen” :
math.aalto.fi/˜apiola/matlab/opas/lyhyt/grafiikka.html#complexplotTässä lyhyesti:
- plot(z) piirtää pisteen z tasoon, jos z on kompleksiluku.
- Yleisemmin, jos z on kompleksivektori, plot(z) piirtää z-vektorin pisteiden kautta murtoviivan.
- Jos halutaan pelkät pisteet, niin plot(z,’o’) (tai esim plot(z,’xb’) jos sinisellä ristillä). - 3. mlK003.tex
Olkoon z:lla edellisen tehtävän arvo. Suorita komennot ja selvitä aina itsellesi, mitä kukin tekee.>> z=sign(z)
>> w=[z,z^2,z^3,z^4,z^5,z^6,z^7,x^8]
>> plot(w)
>> axis equalPiirrä samaan kuvaan säteet origosta kuhunkin w-vektorin pisteeseen vaikka punaisella.
Vihje: Muista hold on ja sitten vaan annat plot:lle argumentiksi 2:n pituisia vektoreita ja käytät komentoeditoria (napsuttelet nuolinäppäintä ja editoit).Mitä havaitset, jos ajattelet kompleksiluvun potensseja (vaikkapa De Moivreta)?
Matlab-tekniikkaa:
- Miksi ei tarvitse kirjoittaa z.^2 ?
- Entä jos haluaisit piirtää potenssit 1:100 ? Miksi nyt täytyy kirjoittaa .^ ?Suorita Matlab:ssa: help arith
Lue: .../opas/ei-niin-lyhyt/osa2.html#luku4 matriisi- ja taulukko-operaatioesimerkit ja
...opas/lyhyt/perusteet.html#sec:matriisilaskenta - 4. mlK004.tex
Muodosta vektori, jossa on luvut wn,k =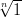 ,k = 0…n − 1. n:n arvolla 10.
,k = 0…n − 1. n:n arvolla 10.
a) Käytä juurikaavoja.
b) Ratkaise (numeerisesti) polynomiyhtälö zn = 1 ( help roots)Piirrä yksikköympyrä ja samaan kuvaan kaikki ykkösen n:nnet juuret vaikka ’o’-merkillä), missä vaikkapa n = 10. Kokeile eri n:n arvoilla.
Kirjoita Matlabin editorilla tiedosto h1teht3.m (tms.) ja tee siitä Matlab skripti tyyliin:
% Harjoitus 1 tehtävä 3 , tiedosto h1teht3.m
% Nimi ja opno (harjoitukseksi myöhempiin tarpeisiin)
%
n=10 % Tätä voit vaihdella.
k=0:n-1 % kokonaislukuvektori.
w=... % w-vekori, jossa nuo n:nnet juuret.
Skripti, jossa on Matlab-komentoja (ja selityksiä %-merkin takana), suoritetaan Matlabissa komentamalla h1teht3 tai leikkaus/liimaus- menetelmällä. Suosittelemme jälkimmästä myös siksi, että lienee yksinkertaisinta sijoittaa tärkeimmät komentojen tulokset samaan tiedostoon, jolloin sitä ei enää voi suorittaa skriptinä (ellei halua nähdä virheilmoitussumaa).
- 5. mlK005.tex
Puhdas kynä/paperi-tehtävä. Hahmottele seuraavat alueet kompleksitasossa (z-tasossa) ja niiden kuva- alueet kuvauksessa w = ez. Kiinnitä myös huomiota siihen, kuuluuko reuna mukaan. Tässä z = x + iy
(a) −1 < x < 1,−π < y < π.
(b) 0 ≤ y ≤ π∕2. (Mieti, kuuluuko 0 mukaan kuvaan.)
(c) π < y ≤ 3π.
(d) ln 3 < x < ln 5. - 6. mlK006.tex
Avaa
http://www.math.hut.fi/teaching/k3/03/L/CA1.html
ja sieltä kohta demoexp. Voit käytellä skriptiä leikkaamalla/liimaamalla omaan Matlab-työtiedostoosi ja sieltä komentoikkunaan. Tässä vaiheessa ei ole välttämätöntä ymmärtää kaikkia skriptin Matlab-komentoja, kunhan näet, miten sitä modifiomalla voit tehdä haluamiasi juttuja.(a) Suorita ensin komennot ja katso, että saat samanlaiset kuvat kuin CA1.html:ssä.
(b) Havainnollista exp-funktiota katsomalla joidenkin suorakulmioalueiden kuvautumista.
(c) Voit myös helposti muuttaa skriptiä yleisluontoisemmaksi ottamalla x-vektorin pituuden n käyttöön ja kirjoittamalla vastaavanlaisen for-silmukan kuin y-vektorille on tehty. - 7. mlK007.tex
(Puhdas käsinlasku)
Kompleksiluvulla eiα kertominen suorittaa kierron kulman α verran. Kyseessä on tason ℝ2 lineaarikuvaus, jolla niin ollen on matriisiesitys. (Muistele 1-kurssien asioita, lineaarikuvauksia käsitellään tälläkin kurssilla lähemmin.)Johda kiertokuvauksen matriisiesitys muodostamalla tulo w = eiαz, z = x + iy = reiΘ
Ohje: Ei tarvitse muuta kuin kirjoittaa eiα(x + iy) muotoon Re + iIm ja samaistaa kompleksiluku x + iy pystyvektorin [x,y]T kanssa.
Opetus: Kiertokuvauksia (ja eräitä muitakin tason lineaarikuvauksia) voidaan käsitellä erityisen kätevästi kompleksiaritmetiikan avulla. Matriisilaskujen sijasta voidaan harrastaa kompleksiaritmetiikkaa.
Seuraavassa tehtävässä harrastetaan tätä oikein olan takaa.
Olennaista on, että käytössä on ohjelma, joka osaa laskea kompleksisilla vektoreilla. Matlab on tällainen (myös Maple ja Mathematica).
- 8. mlK008.tex
Alla on versio kuuluisan matemaatikon Arnoldin ns. kissaa, jonka toteutamme Matlabilla varsin yksinkertaisena tyylitelmänä. Harjoituksen ajatuksena on demonstroida kompleksiaritmetiikan mahdollisuuksia kiertokuvauksien käsittelyssä. Samalla saamme rutiinia niin Matlabissa kuin yleensäkin kompleksiluvuilla laskemisessa.Käsittelemme tässä kissaa tavallisuudesta poiketen kompleksilukuvektorina.
Tehtävässä ei ole jätetty juurikaan itse keksittävää. Niinpä jos aika on tiukalla, tämä tehtävä sopii oikein hyvin omatoimisesti läpikäytäväksi vaikka kotona.
Selvitä itsellesi juurta jaksain, mitä kussakin vaiheessa tehdään. Kissa ja sen pyöritys on pelkkää kompleksiaritmetiikkaa.
Komennot on annettu “ideointiyyliin”, siksi koodia on niin paljon.
Suorita ensin nämä komennot: (Huomaa puolipisteen käyttö, jos dataa on “vähänkin paljon”.)
clf % clear graphics
t=0:pi/100:2*pi; % tai esim. t=linspace(0,2*pi);
paa=.1*exp(i*t);
plot(paa)
axis equal
hold on
silmat=[-0.05+i*.055, 0.05+i*.055]
plot(silmat,’+’)
nena=.02*i+.003*exp(i*t);% t-vektori muodostettiin yllä.
plot(nena,’r’)
%nena=.02*i
%plot(nena,’o’) % Tämä olisi ‘‘laiskan miehen nenä’’
% Suuksi sopiva ympyrän kaari välillä (-2*pi/3,-pi/3)
phi=linspace(-2*pi/3,-pi/3);
suu=0.05*exp(i*phi);
plot(suu,’.’)
korvat=[.1*exp(i*pi/6),.1*exp(i*5*pi/6)]
plot(korvat,’o’) % ‘‘Laiskan miehen korvat’’Tässä on peruskissa.
Nyt ryhdymme pyörittelemään kissaparkaa. Päätä ei tarvitse pyörittää, ympyrä ei pyöritettäessä miksikään muutu. Riittää, kun pyöritämme suuta, nenää, silmiä ja korvia.
Kootaan ensin kissan osat yhteen vektoriin ja tehdään äskeinen uudestaan kissavektorilla.
figure(1) % Tätä tarvitaan vain palattaessa takaisin kuvasta 2.
% Ajatellaan, että figure(1) on z-taso ja figure(2) w-taso.
clf % Grafiikan putsaus
t=0:pi/100:2*pi; % Syytä tehdä uudestaan, vanha t voisi olla jo ihan muuta
paa=.1*exp(i*t); % vaikkei näillä komennoilla satukaan.
plot(paa)
axis equal
hold on
zkissa=[silmat,nena,korvat,suu];
plot(zkissa,’or’) % Pelkät pisteet merkillä ’o’ värillä ’r’Avataan uusi grafiikkaikkuna ja piirretään siihen kierrettyjä kissoja.
figure(2) % w-taso
clf
wkissa=exp(i*pi/4)*zkissa
paa=.1*exp(i*t);
plot(paa)
axis equal
hold on
plot(wkissa,’or’)
shg % show graphicsNyt voit jatkaa kissaleikkiä alla olevaan tyyliin tai jotenkin muuten. Helpointa ja opettavaisinta on kirjoittaa Matlabin editorilla alla olevat rivit (ja mahdollisesti myös zkissarivit) omien mieltymystesi mukaan modifioiden tiedostoon kissa.m. Kun tiedosto on polun varrella, voit sanoa istunnossasi kissa, editoida kissa.m:ää ja taas komentaa kissaa.
clf
alpha=pi/4; % Kiertokulma, helppo muutella.
wkissa=exp(i*pi/4)*wkissa
paa=.1*exp(i*t);
plot(paa)
axis equal
hold on
plot(wkissa,’or’)
shgSeuraavaksi jo sormet syyhyävät kissan käsittelyyn matriisina ja kiertomatriisilla kerrottuna (vrt. [D]-teht. 5). Maltamme kuitenkin mielemme ja jätämme seuraavaan kertaan.
Palannemme kissaan muutenkin yleisempien lineaarikuvausten yhteydessä, tällöin saatamme kaltoin kohdella sitä paljon enemmän, anteeksi kissa!
- 9. mlK009.tex
Matlab on ennenkaikkea matriisikieli. Jos kompleksiaritmetiikka sujuu käteväti, niin samoin on laita matriisilaskujen. Katsotaan siksi vielä, miten edellinen hoidettaisin matriisioperaatioin. (Vrt. teht. 4) Näin saadaan malli myös yleisemmille linaarikuvauksille.Tällä kerralla esitämme kissan tavanomaisemmassa muodossa kaksirivisenä reaalisena matriisina, jossa kukin sarake edustaa kissan pistettä ℝ2:ssa.
Olkoon zkissa kuten edellä.
alpha=pi/4; % muuttele tarpeen mukaan.
A=[cos(alpha), -sin(alpha);sin(alpha),cos(alpha)] % Kiertomatriisi.
zkissa=[real(zkissa);imag(zkissa)]; % zkissasamaistus C ¡-> R^2
wkissa=A*zkissa; % Mahtavan kätevää on tämäkin. Kun zkissapisteet ovat
% matriisin sarakkeina, niin kertomalla kiertomatriisilla A,
% saadaan wkissapisteiden muodostama matriisi.
figure(1); clf
plot(zkissa(1,:),zkissa(2,:),’o’) % Tämä on kaikkein tavallisin plot-
% komennon muoto, kun data on reaalista.
axis equal
figure(2); clf
plot(wkissa(1,:),wkissa(2,:),’*r’)>> z=2+3*i
z =
2.0000 + 3.0000i
>> plot(z)
>> plot(z,’*’)
>> axis([0 4 0 4])
>> hold on
>> plot([0 z])
>> abs(z)
ans =
3.6056
>> angle(z)
ans =
0.9828
>> atan(3/2)
ans =
0.9828
