
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Tehtäviä differentiaaliyhtälöiden ratkaisemiseen MATLABissa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mlD001.tex (iv3 harj.1 av 2001)
Tätä tehtävää harjoitellaan Matlab-teknisesti loppuviikon harjoituksissa. Osattava esittää (ke 19.9.) liitutaululla käsin piirtäen periaatteessa.Tarkastellaan diffyhtälöä y′ = y − x alueessa −1 ≤ x,y ≤ 1,
Piirrä xy-koordinaatistoon suuntakenttä ja isokliinejä käsin ja kokeile myös Matlabia laskimen roolissa. Ota hilaväliksi aluksi vaikka h = 0.5.
Matlab-laskussa kannattaa muodostaa matriisi, sanokaamme K, jonka alkioina ovat arvot yi − xj, i = 1…5,j = 1…5 tähän tapaan:
h=0.5; t=-1:h:1;x=0:h:2
for i=1:5
for j=1:5
K(i,j)=y(i)-x(j)
end
endKoska matriisissa rivi-indeksi i juoksee alaspäin, on helpompaa sijoittaa arvot koordinaatistoon kääntämällä matriisin sarakkeet ylösalaisin; tämä tapahtuu komennolla flipud. Katso siis matriisista flipud(K) arvot ja merkitse ne kynällä piirrokseen. Tarkista käsin (tai “skalaarilaskimella” (Matlabkin käy)) muutama alkio ainakin. (Hilan tihentäminen käy nyt helposti muuttamalla vain yllä h:ta.)
Myöhemmin opimme, että K-matriisin muodostaminen käy kätevämmin, tehokkaammin ja rutiininomaisemmin näin:x=...;y=... % Kuten edellä
[X,Y]=meshgrid(x,y);
K=Y-X; % Jos esiintyy kertolaskua, potenssia ym.,
% on varustettava pisteellä, siis
% .*, .^ ./ (taulukko-operaatiot)Nyt meillä on kaikki data kerättynä suuntakentän piirtämistä varten. Voit katsoa skriptiä suuntak1.m alla aputiedostossa ja miettiä, mitä siinä tapahtuu. (myös: http://www.math.hut.fi/teaching/v/matlab/suuntak1.m)
Lopuksi voit kokeilla LAODE-funktiota dfield8 (versio v. 2012) , jonka käyttö ei vaadi Matlabin tuntemista lainkaan. http://math.rice.edu/˜dfield/
Avainsanat: matlabDiffyhtälöt, mlbDifferentiaali,suuntakenttä
Viitteet: [LAODE] Golubitzky-Dellnitz: Linear Algebra and Differential Equations using Matlab, Brooks/Cole 1999. - 2. mlD002.tex [vastaava Maple: ...mplD003.tex] (iv3/2001, harj. 1)
Millä xy-tason käyrillä on ominaisuus: Käyrän tangentin kulmakerroin jokaisessa pisteessä (x,y) on −
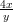 ?
?
Ratkaise yhtälö muuttujien erottelulla (“separation of variables”). Piirrä suuntakenttä isokliineja apuna käyttäen käsin vaikkapa alueessa [−2, 2] × [−2, 2].
Kokeile myös LAODE-funktiota dfield8. Tässä on käytettävä ahkerasti stop-näppäintä, ratkaisu ajautuu aina ongelma-alueelle, mikäli x-akseli on mukana.
Voit myös täydentää kuvaa alussa laskemillasi ratkaisukäyrillä tyyliin:
x=linspace(-2,2,30);y=x; [X,Y]=meshgrid(x,y);
Z=... % muista pisteitt“”aiset laskutoimitukset.
contour(x,y,Z,1:10); shgKokeile ja selitä!
Vihje: Hae m-tiedosto dfield8 sivulta http://math.rice.edu/˜dfield/ ja sijoita se Matlab-polkusi varrelle.
Kirjoita Matlab-istuntoon : dfield8
Avainsanat: MatlabDy, diffyhtälöt, suuntakenttä, isokliinit, mlDifferentiaali(yhtälöt)Viitteet:
[LAODE] Golubitzky-Dellnitz: Linear Algebra and Differential Equations using Matlab, Brooks/Cole 1999.
- 3. mlD0021.tex
Totea, että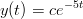
toteuttaa differentiaaliyhtälön y′ = −5y.
Piirrä ratkaisukäyräparvi, kun vakio c saa 21 arvoa tasavälisesti välillä [0,4].
Piirrä paksummalla viivalla alkuehdon y(0) = 1 toteuttava kuvaaja ja merkitse alkupiste rinkulalla.
Vihje:
Ratkaisu:
%% Skripti piirtaa ratkaisukayraparven ...
close all
t= linspace(-.1,.4);
y = exp(-5*t);
plot(t,y);
axis([-.1 .4 0 2])
hold on
for c=linspace(0,4,21)
plot(t,c*y)
end
plot(0,1,’o’)
plot(t,y,’LineWidth’,2)
hold off
title(’Ratkaisuparvi dy:lle y’’(t) = -5 y(t)’) % Huomaa hipsukan(’)kahdennus.Avainsanat: MatlabDiffyht, MatlabODE, diffyhtälöt, ratkaisukayraparvi, Matlab-tekniikkaa
- 4. mlD0021b.tex
Tehtävän mlD0021 b-kohta:
Tee edellinen Matlab:n symbolilaskentakonetta, Mupad:ia käyttäen.Totea Mupad:n avulla suoraan yhtälöön sijoittamalla , että
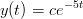
toteuttaa differentiaaliyhtälön y′ = −5y.
Määritä myös diffyhtälön yleinen ratkaisu sekä alkuhdon y(0) = c toteuttava ratkaisu solve-komennolla (kts. vihje)
Piirrä ratkaisukäyräparvi, kun vakio c saa 21 arvoa tasavälisesti välillä [0,4]. (Tai suunnilleen tuonverran)
Piirrä paksummalla viivalla alkuehdon y(0) = 1 toteuttava kuvaaja ja merkitse alkupiste rinkulalla.
Sopii tietysti myös Maplelle, syntaksi muistuttaa läheisesti muPad:ia.
Vihje:
dyhtalo:=ode(y’(t)=-5*y(t),y(t))
aayht:=ode(–y’(t)=-5*y(t),y(0)=c˝,y(t))
ratk:=solve(...)
Y:=op(ratk)
parvi:=plot(Y $ c=0..4 step 1/5,t=-.1..0.4)Grafiikkojen yhdistäminen on laatijalta vielä hakusessa. Maplella display-komennolla.
Ratkaisu:
Avainsanat: MatlabDiffyht, Matlab/muPadODE, diffyhtälöt, ratkaisukayraparvi, Matlab/muPad-tekniikkaa
- 5. mlD003.tex (iv3/2001, harj. 1, teht. 3) (Jatkoa: mlD007.tex)
Lisääntymiskykyinen populaatio, jonka lisääntymistä rajoittavia tekijöitä ei ole, noudattaa yleensä likimain Malthus’n lakia, ts. nykyhetkellä kasvunopeus on verrannollinen populaation nykykokoon.Muodosta ilmiölle differentiaaliyhtälömalli ja ratkaise.
Ratkaisussa esiintyy vakiot y0 = populaation koko alkuhetkellä ja k = ”lisääntymiskykyvakio”.
Täydennämme vanhaa tuttua USA:n väkilukutaulukkoa arvoilla, jossa toinen rivi ilmaisee väkiluvun miljoonissa ja ensimmäinen vuosiluvun.
1800 1830 1860 1890 1920 1950 1980
5.3 13 31 63 106 150 230a) Määritä k kahden ensimmäisen datasarakkeen avulla. Tutki, mihin vuosilukuun saakka malli antaa siedettävän tuloksen ja mistä alkaen sietämättömän.
b) Määritä k ensimmäisen ja viimeisen datasarakkkeen perusteella (jolloin kyseessä ei enää ole tulevaisuuden ennustaminen), ja tutki tämän mallin käyttäytymistä muissa datapisteissä.
c) Havainnollista kuvilla, käytä tarpeen mukaan logaritmista skaalaa.
Vihje: Voit valita ajan 0-hetken vuosiluvuksi 1800 (miksi?). Toki ei mitenkään välttämätöntä.
Avainsanat:MatlabDy, diffyhtälöt, mlDifferentiaali(yhtälöt), populaationkasvumalli, Malthus’n laki
Vastaavanlaisia tehtäviä: http://matriisi.ee.tut.fi/˜piche/ode/ Pichet: TTY 1999, course 73107 (hyvä kokonaisuus):
1) Perusesim tähän kohtaan: In 1980 the population of Altlantia was 254512; in 1995 it was 294726. What is its population in 2000. (Vuosilukuihin voisi lisätä nyt vaikka 15.)
2) Jatkoa: mlD007.tex
- 6. mlD004.tex [Maple-versio: ...mplD004.tex] (iv3/2001, harj. 1, LV teht. 1-2)
Laskuvarjohyppääjän yhtälö. Oletetaan, että hyppääjän + varustuksen massa = m ja ilmanvastus on verrannollinen nopeuden neliöön, olkoon verrannollisuskerroin = b. Tällöin Newtonin 2. laki antaa liikeyhtälön:
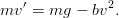
Olkoon yksinkertaisuuden vuoksi m = 1,b = 1 ja g = 9.81m∕s2.
Piirrä suuntakenttä.
Oletetaan, että laskuvarjo aukeaa, kun v = 10m∕s, valitaan tämä alkuhetkeksi t = 0. Piirrä tämä ratkaisukäyrä suuntakenttäpiirrokseen. Yritä nähdä suuntakentästä, että kaikki ratkaisut näyttävät lähestyvän rajanopeutta v ≈ 3.13 ja että ratkaisut ovat joko kasvavia tai pieneneviä (ja millä alkuarvoilla mitäkin, ja mitä tarkoittaa fysikaalisesti)
Määritä rajanopeus suoraan yhtälöstä.
Käytä Matlab-piirroksiin funktiota dfield8 ja Maplessa DEtools-kirjaston DEplot-funktiota.
Vihje: Kts. [HAM] ss. 169-170 tai ?DEplot
> with(DEtools)
> with(plots)Suuntakenttään:DEplot,
grafiikkojen yhdistämiseen: display.
dfield-ohje:
Hae m-tiedosto dfield8 sivulta http://math.rice.edu/˜dfield/ ja sijoita se Matlab-polkusi varrelle.
Kirjoita Matlab-istuntoon : dfield8
Avainsanat: MatlabDy, MapleDy, diffyhtälöt, suuntakenttä, isokliinit, mplDifferentiaali(yhtälöt), mlDifferentiaali(yhtälöt)
Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998
- 7. mlD005.tex (Pichet Course 73107)
Määritä diffyhtälön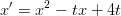
Mikä on tämän funktion minimipisten likiarvo (vaikka 2:n tai 3:n numeron tarkkuudella).Vihje: Hae m-tiedosto dfield8 sivulta http://math.rice.edu/˜dfield/ ja sijoita se Matlab-polkusi varrelle.
Kirjoita Matlab-istuntoon : dfield8
Kun sinulla on yhtälö, suuntakenttä ja ratkaisukäyrä, voit valita Edit/Zoom in, jolla pääset tarkentamaan minipisteen hakua (askeleen kerrallaan).
Ennen minimin hakua kannattaa poistaa piirtämäsi ratkaisukäyrät Options/Erase solutions, niin Options/Keyboard input-valinnalla voit antaa tarkan alkuarvon.Avainsanat:MatlabDy, diffyhtälöt, mlDifferentiaaliyhtälöt, suuntakenttä, dfield8
- 8. mlD006.tex
Kun Marsiin laskeutuvan luotain laukaisee laskeutumisrakettinsa, sen nopeutta kuvaa differentiaaliyhtälö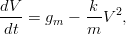
missä gm = 3.688 on Marsin painovoimakerroin, k = 1.2 on aerodynaaminen vastusvoima, ja m = 150 on luotaimen massa kilogrammoissa. Käytä vapaan pudotuksen rajanopeutta alkuarvona (Marsissa rajanopeus on 67.056 m/s), ja ratkaise yhtälö välillä [0 : 0.05 : 6]. Piirrä sekä nopeuden että kiihtyvyyden kuvaajat. Vihje:
- 9. mplD017.tex, mlD007.tex
Huomasimme, että eksponentiaalinen kasvumalli, ns. Malthus’n laki y′ = ky ei toimi USA:n väestödataan pitkällä aikavälillä. Mallia voidaan tarkentaa lisäämällä sopiva kasvua rajoittava termi, tällöin johdutaan ns. logistiseen kasvulakiin:y′ = ay − by2
USA:n väestödataan liityen Verhulst arvioi v. 1845 arvot a = 0.03 ja b = 1.610−4, kun t mitataan vuosissa ja väkiluku y(t) miljoonissa.
Opettajalle: Tehtävä voidaan käsitellä ehkä luontavamminkin kokonaan erillisenä numeeristen diffyhtälöratkaisujen opetuksesta. Tällöin otetaan vain alla olevat kohdat (c) ja/tai (d).
(a) Ratkaise tehtävä (y(0) = 5.3) Eulerin menetelmällä käyttämllä askelpituussa h = 10
(b) rk4:llä käyttäen n. nelinkertaista askelta (voit kokeilla pienempiäkin)
(c) Matlabin ode45:llä.
(d) Laske analyyttinen ratkaisu Maplella (kyseessähän on Bernoullin yhtälö.
Piirrä kuvia ja laske kaikissa tapauksessa ratkaisujen arvot annetuissa taulukkopisteissä. (ode45-tapauksessa onnistuu ainakin sovittamalla dataan splini funktiolla spline, joka on maailman helppokäyttöisin.)
kts. http://www.math.hut.fi/teaching/v/matlab/opas.html#splinit
(Nykyään (2012) ei tarvita erillistä splinisovitusta, laskentapisteet voidaan antaa suoraan ode45-funktiolle syötteenä.) Vihje:function [T,Y]=eulerS(f,Tspan,ya,n)
% Tämä vain kehittely- ja opettelutarkoituksessa.
% Funktio eulerV hoitaa niin skalaari- kuin vektoriversion.
% (24.2.04, modifioitu 21.8.2010)
% Esim: y’=t+y, y(0)=1
% f=@(t,y)t+y
% [T,Y]=eulerS(f,[0 4],1,6), plot(T,Y,T,Y,’.r’);shg
a=Tspan(1);b=Tspan(2);
h=(b-a)/n;
Y=zeros(n+1,1);T=(a:h:b)’; %Pystyvektorit yhdenmukaisesti ode45:n
Y(1)=ya; % kanssa
for j=1:n
Y(j+1)=Y(j)+h*f(T(j),Y(j));
end;Viitteitä:
http://math.aalto.fi/opetus/kp3-ii/06/L/L14dynumkalvot.pdf
http://www.math.hut.fi/˜apiola/matlab/opas/lyhyt/esim/eulerS.m
(Listaus yllä) - 10. mlD008.tex,mplD018.tex
Tarkastellaan yhtälöä y′ = −2α(t − 1)y. Ratkaise aluksi analyyttisesti (saat käyttää Mapleakin.)Totea kuvasta ja derivaattaehdosta yhtälön stabiilisuus/epästabiilisuusalueet. Ota kuvassa ja aina tarvittaessa vaikkapa α = 5.
Ratkaise yhtälö sekä Eulerilla että BE:llä. Sopivia arvoja voisivat olla vaikkapa h = 0.2, väli: [1, 4.5], y(1) = 1.
Vertaa kokeellisesti stabiilisuukäyttäytymistä teorian ennustamaan ja pane merkille, miten epästabiilisuus käytännössä ilmenee.
Tämä tehtävä soveltuu erityisen hyvin Maplella tehtäväksi, se on pitkälle ideoitu [HAM] sivulla 124, myös Euler ja BE ovat valmiina. (Koodit saa kurssin maple-hakemistosta.) ** Tulee aputiedostoon **** apu puuttuu, editoi viitteet! ** Vihje:
Viitteitä:
http://math.aalto.fi/opetus/kp3-ii/06/L/L14dynumkalvot.pdf
http://www.math.hut.fi/˜apiola/matlab/opas/lyhyt/esim/eulerS.m
(Listaus yllä) - 11. Ratkaise differentiaaliyhtälö
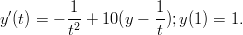
käyttäen Backward-Euler menetelmää:
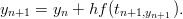
Jotta tämä onnistuisi, tulee jokaisella iteraation askeleella ratkaista yhtälö
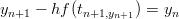
yn+1:n suhteen. Tämä tarkoittaa, että yleisen ratkaisimen kirjoittaminen olisi vaikeaa, mutta tässä eksplisiittisessä tapauksessa se onnistuu.
Vertaa sitten saamaasi tulosta MATLABin ode45 funktiolla saamaasi: kuinka selität eron? Vihje:
- 12. Maple,Matlab (H2T10)
- Ratkaise alkuarvotehtävä
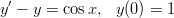
analyyttisesti Maplella ja numeerisesti Matlabilla. Piirrä ratkaisukäyrä.
- Anna alkuarvoksi symboli c ja piirrä ratkaisukäyräparvi sopivalla välillä,
kun c = −0.9,−0.8,…, 0.
Miltä parvi näyttää suurilla x :n arvoilla. Tässä pitäisi erottua kolmenlaista käytöstä.
Vihje: Maple: dsolve, Matlab: ode45
Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu.
- Ratkaise alkuarvotehtävä
- 13. mplD007.tex (iv3/2001, harj. 2, AV teht. 1)
Ratkaise (AA)-tehtävä y′− 2xy = 1, y(0) = −0.5Tässä näyttää siltä, että (EHY):n erikoinen olisi helppo löytää, mutta huomaat pian, että luonnolliset yritteet eivät toimi. (Kyseessähän on lineaarinen, mutta ei-vakiokertoiminen yhtälö.)
Ratkaise vaan sitten kiltisti integroivan tekijän menettelyllä.
Integrointi johtaa erf-funktioon, Maple antaa sen suoraan, voit myös konsultoida KRE-kirjaa hakusanalla erf. Lausu siis ratkaisu erf:n avulla.
Piirrä suuntakenttäpiirros Maplen DEtools-pakkauksen DEplot-funktion avulla (kts [HAM] s. 169), voit toki käyttää myös Matlab:n dfield8-funktiota (ohje alla).
Valitse alkuarvoja y0 väliltä (−1,−0.5) yrittäen löytää kriittistä arvoa y0, joka jakaa ratrkaisukäyrät plus tai miinus ääretöntä lähestyviin. (Tuo kriittinen ratkaisukäyrä on rajoitettu.) Käytä hyväksesi erf-funktion ominaisuutta lim x→∞erf(x) = 1 laskeaksesi tarkan arvon y0:lle.
Vihje: dfield-ohje: Hae m-tiedosto dfield8 sivulta http://math.rice.edu/˜dfield/ ja sijoita se Matlab-polkusi varrelle.
Kirjoita Matlab-istuntoon : dfield8
Avainsanat: MapleDy, diffyhtälöt,erf, mplDifferentiaali(yhtälöt)
Viitteet: [KRE] E. Kreyszig: Advanced Engineering Mathematics, Wiley
[HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998. - 14.
- Piirrä tasokäyrä (x,y) = (e−t∕20 cos t,e−t∕10 sin t) (faasitaso).
- Piirrä edelliset koordinaattikäyrät x(t) ja y(t) (aikataso).
Vihje: Muista (.*), kun muodostat vektorilausekkeita. kokeile eri parametrivälejä. Kokeile linspace(a,b,n):ssä muitakin kuin oletusarvoa n = 100. Käytä axis-komentoa. Ja kysele help:llä.
Uusi grafiikkaikkuna: >> figure, Useampia samaan kuvaan: >> hold onAvainsanat: Differentiaaliyhtälöryhmä, aikakuva,faasikuva,grafiikka,plot
- Piirrä tasokäyrä (x,y) = (e−t∕20 cos t,e−t∕10 sin t) (faasitaso).
- 15. Kun Marsiin laskeutuvan luotain laukaisee laskeutumisrakettinsa, sen nopeutta kuvaa differentiaaliyhtälö
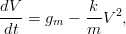
missä gm = 3.688 on Marsin painovoimakerroin, k = 1.2 on aerodynaaminen vastusvoima, ja m = 150 on luotaimen massa kilogrammoissa. Käytä vapaan pudotuksen rajanopeutta alkuarvona (Marsissa rajanopeus on 67.056 m/s), ja ratkaise yhtälö välillä [0 : 0.05 : 6]. Piirrä sekä nopeuden että kiihtyvyyden kuvaajat. Vihje:
- 16. Ratkaise toisen kertaluvun alkuarvotehtävä
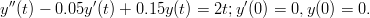
Vihje: Voi olla avuksi määritellä y1 = y,y2 = y′, jolloin toisen kertaluvun tehtävä muuttuu ensimmäisen kertaluvun systeemiksi
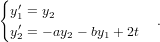
- 17. Eulerin menetelmä on klassinen menetelmä differentiaaliyhtälöiden ratkaisemiseksi. Menetelmän lähtökohtana on yhtälö
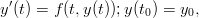
josta koetetaan ratkaista y(t) kun t = [t0,tn]. Menetelmä perustuu t:n diskretoinnille: t muunnetaan joksikin vektoriksi T = (t0,t0 + h,…,tn), jonka jälkeen koetetaa etsiä vastaavia arvoja y(t0 + ih). Merkintöjen selvyyden vuoksi kirjoitetaan t0 + jh = tj. Eulerin menetelmässä approksimoidaan arvoa y(ti) seuraavasti:
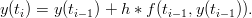
Ratkaise Eulerin menetelmällä differentiaaliyhtälö
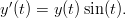
Käytä eri h:n arvoja, ja vertaa oikeaan ratkaisuun e1−cos(t). Vihje: Eulerin menetelmä MATLABissa on helpointa toteuttaa yksinkertaisena silmukkana. Olettaen, että yhtälön oikea puoli on kirjoitettu funktioon f(t,y), Euler-iteraatio voidaan tehdä seuraavasti:
for n = 2:length(t)
y(n) = y(n-1)+h*f(t(n-1),y(n-1));
endmissä t on vektori joka on ratkaisuvälin diskretointi, ja h on t:n pisteiden välinen etäisyys.
- 18. Rungen-Kutan menetelmä differentiaaliyhtälöiden ratkaisemiseksi on huomattavasti kehittynyt versio Eulerin menetelmästä. Menetelmässä määritellään seuraavasti:
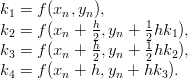
Diskretointiaskeleeksi tulee nyt
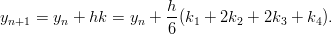
- Ratkaise edellisen tehtävän yhtälö
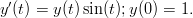
käyttämällä Rungen-Kutan menetelmää. Vertaa tulosta sekä todelliseen ratkaisuun y(t) = e1−cos(t), että Eulerin menetelmällä saavutettuun. Mitä huomaat tarvittavasta askelkoosta?
- Ratkaise alkuarvotehtävä
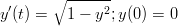
käyttämällä Rungen-Kutan menetelmää.
- Ratkaise edellisen tehtävän yhtälö
- 19. Ratkaise toisen kertaluvun alkuarvotehtävä
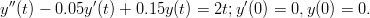
Vihje: Voi olla avuksi määritellä y1 = y,y2 = y′, jolloin toisen kertaluvun tehtävä muuttuu ensimmäisen kertaluvun systeemiksi
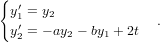
- 20. Eulerin menetelmä on klassinen menetelmä differentiaaliyhtälöiden ratkaisemiseksi. Menetelmän lähtökohtana on yhtälö
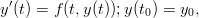
josta koetetaan ratkaista y(t) kun t = [t0,tn]. Menetelmä perustuu t:n diskretoinnille: t muunnetaan joksikin vektoriksi T = (t0,t0 + h,…,tn), jonka jälkeen koetetaa etsiä vastaavia arvoja y(t0 + ih). Merkintöjen selvyyden vuoksi kirjoitetaan t0 + jh = tj. Eulerin menetelmässä approksimoidaan arvoa y(ti) seuraavasti:
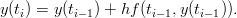
Ratkaise Eulerin menetelmällä differentiaaliyhtälö
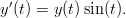
Käytä eri h:n arvoja, ja vertaa oikeaan ratkaisuun e1−cos(t). Vihje: Eulerin menetelmä MATLABissa on helpointa toteuttaa yksinkertaisena silmukkana. Olettaen, että yhtälön oikea puoli on kirjoitettu funktioon f(t,y), Euler-iteraatio voidaan tehdä seuraavasti:
for n = 2:length(t)
y(n) = y(n-1)+h*f(t(n-1),y(n-1));
endmissä t on vektori joka on ratkaisuvälin diskretointi, ja h on t:n pisteiden välinen etäisyys.
- 21. Rungen-Kutan menetelmä differentiaaliyhtälöiden ratkaisemiseksi on huomattavasti kehittynyt versio Eulerin menetelmästä. Menetelmässä määritellään seuraavasti:
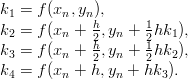
Diskretointiaskeleeksi tulee nyt

- Ratkaise edellisen tehtävän yhtälö
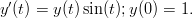
käyttämällä Rungen-Kutan menetelmää. Vertaa tulosta sekä todelliseen ratkaisuun y(t) = e1−cos(t), että Eulerin menetelmällä saavutettuun. Mitä huomaat tarvittavasta askelkoosta?
- Ratkaise alkuarvotehtävä
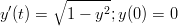
käyttämällä Rungen-Kutan menetelmää.
- Ratkaise edellisen tehtävän yhtälö
- 22. mlD105.tex
Ratkaise differentiaaliyhtälöryhmä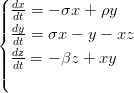
numeerisesti välillä [0, 20], kun σ = 10,ρ = 28 ja β = 8∕3. Piirrä ratkaisukäyrät samaan kuvaan, ja piirrä käyrät x(t) ja z(t) parametrisesti. Tämän jälkeen piirrä 3-ulotteinen parametrisoitu käyrä kaikista koordinaateista.
Onko ratkaisu rajoitettu? Suppeneeko se kohti jotain arvoa?
Kokeile muuttaa alkuarvoja, sekä parametrien arvoja. Vallitsevan teorian mukaan systeemi on kaoottinen dynaaminen systeemi, jonka käyttäytyminen voi muuttua merkitsevästi jo pienistä muutoksista lähtötilanteessa; itse asiassa termi perhosvaikutus keksittiin kuvaamaan juuri tämän systeemin käytöstä. Vihje: Kolmiulotteinen parametrisoitu käyrä (tai pistejoukko) piirretään MATLABissa funktiolla plot3.
- 23. Kirjoita heiluriyhtälö Θ′′ +
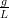 sin(Θ) = 0 ensimmäisen kertaluvun systeemiksi ja
samantien Matlab-funktioksi (joko inline tai m-tiedosto). Voit ottaa g∕L = 1.
sin(Θ) = 0 ensimmäisen kertaluvun systeemiksi ja
samantien Matlab-funktioksi (joko inline tai m-tiedosto). Voit ottaa g∕L = 1.
Laske ratkaisu sopivalla aikavälillä (esim.
![[0,10]](matlabHarDY31x.png) ) ja kolmella erilaisella alkuarvolla,
joilla saat erityyppiset ratkaisut. Käytä ode45-funktiota.
) ja kolmella erilaisella alkuarvolla,
joilla saat erityyppiset ratkaisut. Käytä ode45-funktiota.
Piirrä ratkaisukäyrät aikatasoon ja trajektorit faasitasoon.
- 24. Reuna-arvotehtävä tähtäysmenetelmällä (Moler odes teht. 7.19 ss. 45–47.) Olkoon ratkaistavana reuna-arvotehtävä y′′ = y2 − 1, y(0) = 0, y(1) = 1. Tee Matlab-funktio, joka ottaa argumentikseen ”alkunopeuden” 0:ssa ja palauttaa vastaavan AA-tehtävän ratkaisun arvon 1:ssä, vähennä siitä vielä 1, niin sinulla on funktio, jota sopii tarjota fzero:lle.
- 25. Ratkaise differentiaaliyhtälö
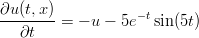
nelikulmiossa [0, 5] × [−2, 2], alkuarvokäyrällä u(0,x) = e−x2.
Piirrä tuloksista kuva:
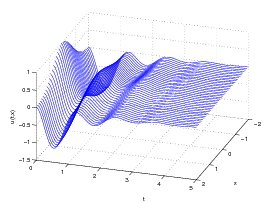 Vihje: Määrittele ensin sopivan harva diskretaatio välille [−2,2], ja sen jälkeen tähän
diskretaatioon sopiva alkuarvokäyrä, sen jälkeen ratkaise differentiaaliyhtälö numeerisesti (ode45)
vuoroittain kullekin alkuarvolle.
Vihje: Määrittele ensin sopivan harva diskretaatio välille [−2,2], ja sen jälkeen tähän
diskretaatioon sopiva alkuarvokäyrä, sen jälkeen ratkaise differentiaaliyhtälö numeerisesti (ode45)
vuoroittain kullekin alkuarvolle.
- 26. Ratkaise nk. Rösslerin systeemi
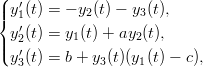
missä a,b,c ovat parametreja, välillä t ∈ [0, 100]. Käytä alkuarvoja y(0) = [1, 1, 1]T ja (a,b,c) = (0.2, 0.2, 2.5).
Kyseessä on kaoottinen systeemi, ts. ratkaisurata riippuu suuresti joko alkuarvoista ja parametreista. Saatuasi ratkaisun, piirrä ratkaisun kuvia alkuarvon muuttujana, ja tutki kuinka pienet muutokset aiheuttavat havaittavia eroja.
- 27. Tässä tehtävässä mallinnetaan lyijyn kulkeutumista elimistöön ja sieltä pois. Ratkaistavaksi tulee epähomogeeninen differentiaaliyhtälöryhmä.
Taustaa. Lyijyä kulkeutuu ihmiselimistöön hengityksen, ruoan ja juoman kautta. Keuhkoista ja vatsalaukusta lyijy kulkeutuu nopeasti verenkierron mukana maksaan ja munuaisiin, ja imeytyy edelleen hitaasti muihin pehmytkudoksiin ja hyvin hitaasti luustoon. Se kulkeutuu elimistöstä pois pääasiassa virtsan mukana, mutta myös hikoilun, hiusten ja kynsien kautta (ks. kuva):
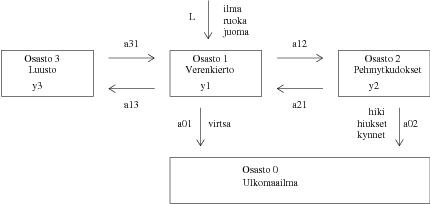
Mallinnamme ihmiselimistöä eri osastoina (veri, pehmytkudokset, luusto). Funktio xi(t) (i = 1, 2, 3) merkitsee lyijypitoisuutta osastossa i hetkellä t. Pitoisuuden yksikkö on mikrogramma ja ajan vuorokausi. Oletamme, että lyijyn virtausnopeus osastosta i osastoon j on suoraan verrannollinen pitoisuuteen xi(t) kertoimella aji > 0. Ulkomaailmalle on oma osastonsa, jotta mallista saadaan mielekäs, mutta emme ole kiinnostuneita ulkomaailman lyjypitoisuuksista. Lisäksi oletamme, että lyijyn virtaus ulkomaailmasta elimistöön tapahtuu vakionopeudella L – tämä ilmenee yhtälöryhmän oikeana puolena kuten pakottava voima massa-jousi-systeemeissä eikä siis liity ulkomaailman osastoon.
1. Matriisimuotoilu. Edellisen sivun mallista saadaan epähomogeeninen differentiaaliyhtälöryhmä
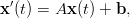
(1) missä
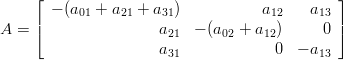
ja b = (L, 0, 0).
- Selitä edellisen sivun mallin perusteella miksi matriisi A ja vektori b ovat kuten yllä.
- Miksi matriisi A on aina kääntyvä? (Ks. Matlab-tiedosto.)
- Etsi differentiaaliyhtälöryhmälle (1) erityisratkaisu xe(t).
2. Käytännön esimerkki. Tutkijat mittasivat pitkän aikavälin lyijypitoisuuksia vapaaehtoisen, terveen kaupunkilaismiehen (Los Angeles) veressä, luustossa ja kudoksissa. Mittausten pohjalta saatiin L = 49, 3 mikrogrammaa / päivä ja seuraava taulukko (yksikkönä 1/päivä):
a21 = 0, 011, a12 = 0, 012 (verestä kudoksiin ja takaisin) a31 = 0, 0039, a13 = 0, 000035 (verestä luihin ja takaisin) a01 = 0, 021, a02 = 0, 016 (poistuma verestä ja kudoksista) - Syötä ylläolevat arvot matriisiin A.
- Laske uudelleen kohdan 1 yksittäisratkaisu xe.
- Etsi homogeeniselle differentiaaliyhtälöryhmälle x′(t) = Ax(t) yleinen ratkaisu xh(t).
- Mikä on epähomogeenisen differentiaaliyhtälöryhmän (1) yleinen ratkaisu?
- Ratkaise (1) alkuarvolla x(0) = 0, ts. määritä kehon lyijypitoisuudet ajan funktiona tapauksessa, jossa henkilö on juuri muuttanut Los Angelesiin keho vailla lyijyä.
- 28. Kirjoita heiluriyhtälö Θ′′ +
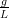 sin(Θ) = 0 ensimmäisen kertaluvun systeemiksi ja
samantien Matlab-funktioksi (joko inline tai m-tiedosto). Voit ottaa g∕L = 1.
sin(Θ) = 0 ensimmäisen kertaluvun systeemiksi ja
samantien Matlab-funktioksi (joko inline tai m-tiedosto). Voit ottaa g∕L = 1.
Laske ratkaisu sopivalla aikavälillä (esim.
![[0,10]](matlabHarDY39x.png) ) ja kolmella erilaisella alkuarvolla,
joilla saat erityyppiset ratkaisut. Käytä ode45-funktiota.
) ja kolmella erilaisella alkuarvolla,
joilla saat erityyppiset ratkaisut. Käytä ode45-funktiota.
Piirrä ratkaisukäyrät aikatasoon ja trajektorit faasitasoon.
- 29. Reuna-arvotehtävä tähtäysmenetelmällä (Moler odes teht. 7.19 ss. 45–47.) Olkoon ratkaistavana reuna-arvotehtävä y′′ = y2 − 1, y(0) = 0, y(1) = 1. Tee Matlab-funktio, joka ottaa argumentikseen ”alkunopeuden” 0:ssa ja palauttaa vastaavan AA-tehtävän ratkaisun arvon 1:ssä, vähennä siitä vielä 1, niin sinulla on funktio, jota sopii tarjota fzero:lle.
- 30. Maple,Matlab (H2T10)
- Ratkaise alkuarvotehtävä
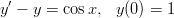
analyyttisesti Maplella ja numeerisesti Matlabilla. Piirrä ratkaisukäyrä.
- Anna alkuarvoksi symboli c ja piirrä ratkaisukäyräparvi sopivalla välillä,
kun c = −0.9,−0.8,…, 0.
Miltä parvi näyttää suurilla x :n arvoilla. Tässä pitäisi erottua kolmenlaista käytöstä.
Vihje: Maple: dsolve, Matlab: ode45
Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu.
- Ratkaise alkuarvotehtävä
- 31. Ratkaise differentiaaliyhtälö
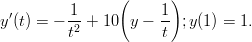
käyttäen Backward-Euler menetelmää:
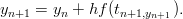
Jotta tämä onnistuisi, tulee jokaisella iteraation askeleella ratkaista yhtälö
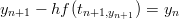
yn+1:n suhteen. Tämä tarkoittaa, että yleisen ratkaisimen kirjoittaminen olisi vaikeaa, mutta tässä eksplisiittisessä tapauksessa se onnistuu.
Vertaa sitten saamaasi tulosta MATLABin ode45 funktiolla saamaasi: kuinka selität eron? Vihje:
