
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Maple harjoitustehtäviä liittyen perusaritmetiikkaan kanssa toimimiseen Maplessa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mplV000.tex
Ohjeita
Kerätään ohjeita näiden tehtävien aihepiiriin liittyen. “Tehtävä”-linkistä saat LATEX-koodin, josta sopivan osan voit haluamallasi tavalla muokaten liittää tehtäväpaperiisi.
Taylorin polynomit
Kahden muuttujan Taylorin polynomi kehitettynä pisteesä p voidaan kirjoittaa:
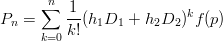
Tästä on helppo arvata, miten useamman muuttujan polynomi rakentuu.
Erityisesti 2. asteen Taylorin kaava voidaan kirjoittaa muotoon
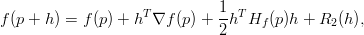
Neliömuotojen definiittisyys
Määr: Neliömuoto q(x) = xT Ax (A on symmetrinen matriisi) on
- 1.
- positiivisesti definiitti, jos q(x) > 0 ∀x≠0,
- 2.
- negatiivisesti definiitti, jos q(x) < 0 ∀x≠0,
- 3.
- positiivisesti semidefiniitti, jos q(x) ≥ 0 ∀x ∈ ℝn ja ∃y≠0, jolla q(y) = 0,
- 4.
- negatiivisesti semidefiniitti, jos q(x) ≤ 0 ∀x ∈ ℝn ja ∃y≠0, jolla q(y) = 0,
- 5.
- indefiniitti, jos ∃x,y siten, että q(x) > 0 ja q(y) < 0.
Samoja definiittisyyskäsitteitä käytetään myös symmetrisestä matriisista A.
Suunnattu derivaatta ja gradientti
- Suunnattu derivaatta pisteesä p0 vektorin v suunassa saadaan lasketuksi pisteessä p0 lasketun gradientin ja suuntayksikkövektorin sisätulona.
- Siispä funktio kasvaa nopeimmin gradientin suuntaan ja sen kasvu on 0 gradienttia vastaan kohtisuoraan suuntaan.
- Suunta, johon funktion kasvu on 0 on tasa-arvokäyrän (tai -pinnan) tangentin (tangenttitason) suuntainen, joten gradientti on normaalin suuntainen.
Pinnan normaali ja tangenttitaso
Jos pinnan yhtälö esitetään muodossa F(x,y,z) = 0, saadaan edellisen perusteella pinnan tangenttitason yhtälö pisteessä p0 näin:
∇F(p0)(p − p0) = 0
Jos pinta on annettu muodossa z = f(x,y), saadaan siten normaalin suunta funktion F(x,y,z) = f(x,y) − z gradienttina.
Tästä seuraa, että pisteeseen p0 asetetun tangenttitason yhtälö voidaan kirjoittaa muotoon
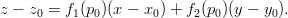
(f1ja f2 tarkoittavat osittaisderivaattoja.)
Kahden pinnan leikkauskäyrän tangentti
Leikkauskäyrän tangentti on kohtisuorassa molempien pintojen normaalia vastaan (eikö vain!). Siten leikkauskäyrän tangentin suuntainen vektori saadaan pinnan normaalivektorien ristitulona t = n1 × n2.
Kriittiset pisteet, ääriarvot
Kriittinen piste (KRP) p: ∇f(p) = 0.
Kriittisen pisteen laatu selviää (jos selviää) Hessen matriisin Hf(p) definiittisyydestä.
Symmetrisen matriisin definiittisyyskäytös selvitetään ominaisarvojen avulla. Jos matriisi on 2 ⋊ 2, voidaan käyttää determinanttia (kts. tehtävä mplV006a). Isommillekin matriiseille on determinanttiehtoja, mutta ne on hankala muistaa ja käyttää, jääkööt muistoksi “determinanttien kulta-ajoilta”.Maple-ohjeita
Vektorikenttä ja gradientti
with(linalg): with(plots):
fieldplot(grad(f(x,y),[x,y]),x=a..b, y=c..d,arrows=slim,color=x);
# a:lla, b:lla jne. oltava tietysti numeeriset arvot.Uusissa Maplen versioissa on kirjastopakkaus VectorCalculus ja siellä funktio Gradient lukuisine valitsimineen. Kts. helppi. Vanhan linalg-kirjaston kunnon grad on perustarpeisiin ehkä yksinkertaisin ja helppokäyttöisin.
Oma pikku funktio on usein selkein, se voidaan määritellä ongelmakohtaisesti esim. toimimaan vain 2d-tilanteessa. Tällainen gradienttifunktio voitaisin kaikessa yksinkertaisuudessaan määritellä näin: gradi2:=(f,x,y)->[diff(f,x),diff(f,y)]
Pintapiirroksen “valaiseminen” esim. avaruuskäyrillä
Usein pintapiirrosta voidaan täsmentää ja tarkentaa ja ymmärtää paremmin, kun piirretään sopivia avaruuskäyriä pinnalle spacecurve:lla.
Alla on esimerkki, jossa piirretään napasädettä pitkin kulkevan pystytason ja annetun pinnan leikkauskäyrä sekä käyrän projektio xy-tasossa. Varsin käyttökelpoinen tapa monessa yhteydessä. Tätä voi modifioida tarpeen mukaan.
with(plots):
f:=(x,y)->4-x^2-y^2;
x:=r*cos(Theta):y:=r*sin(Theta): Theta:=Pi/4:
pystyleikkaus:=spacecurve(–[x,y,f(x,y)],[x,y,0]˝,r=0..2,thickness=3,
color=blue,axes=BOX)
# HUOM! html:ssa edellinen nakyy vaarin, pitaa olla:
# pystyleikkaus:=spacecurve(Aaltoauki[x,y,f(x,y)],[x,y,0]Aaltokii,r=0..2,...)
# missa Aalto tarkoittaa aaltosulkua,
x:=’x’:y:=’y’: # Kannattaa muistaa vapauttaa.
pinta:=plot3d(f(x,y),x=-2..2,y=-2..2):
display([pinta,pystyleikkaus],style=patchcontour,transparency=0.5); - 2. mplV001.tex
Piirrä seuraavien funktioiden tasa-arvokäyrät:- x3 − xy3
- sin(x)cosh(y)
- cos 2(x) cosh(y)
- 3. mplV0011.tex
Mitkä ovat seuraavien funktioiden luonnolliset määrittelyjoukot:
a) f(x,y) =
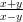 , b) f(x,y) = ln(1 + xy) c) f(x,y) = arcsin(x + y) .
, b) f(x,y) = ln(1 + xy) c) f(x,y) = arcsin(x + y) .
Piirrä (ensin käsin ja sitten Maplella) tasoon kunkin määrittelyjoukon kuva. Mitä topologisia ominaisuuksia joukoilla on? (avoin, suljettu, rajoitettu, yhtenäinen, joukon reuna, jne.)
Muodosta näiden funktioiden korkeuskäyrien (tasa-arvokäyrien) yhtälöt. Muodosta myös pystyleikkauskäyrät tasojen x = 1 ja y = 1 kanssa kussakin tapauksessa. Hahmottele käsin ja piirrä Maplella. Vihje: Tasa-arvokäyriä voi piirtää kommennolla contourplot (ensin with(plots))). Lisää Maple-ohjeita 1. “tehtävässä” mplV000.tex.
- 4. mplV0012.tex
Onko seuraavilla funktioilla raja-arvo, kun (x,y) → (0, 0) :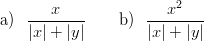
Suorita Maplella visualisointeja. Vihje: Tasa-arvokäyriin: contourplot (ensin with(plots))), pintoihin: plot3d (ei tarvitse latauksia) .
Lisää Maple-ohjeita “tehtävässä”1.(mplV000.tex). - 5. mplV0013.tex
Olkoon f : ℝ2 → ℝ,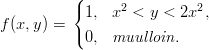
Osoita, että funktiolla on sama raja-arvo origossa lähestyttäessä mitä tahansa suoraa pitkin, mutta siitä huolimatta varsinaista raja-arvoa ei ole olemassa. Missä pisteissä funktio on jatkuva ja missä taas ei?
Suorita Maplella visualisointeja. Vihje: Kulje erityisesti O:sta alkavaa nousevaa sädettä (kulmakerroin posit.) 1. neljänneksessä kulkien sitä alaspäin kohti origoa. Mitä tapahtuu lopulta, kun ollaan riittävän lähellä O:a? Ratkaisu: Piirrä kuvaaja funktion rajoittumasta mielivaltaiselle origon kautta kulkevalle suoralle; tutki tätä varten, missä pisteissä ko. suora leikkaa paraabelit y = x2 ja y = 2x2. Funktio on epäjatkuva näillä paraabeleilla.
- 6. mplV0014.tex
(a) Muodosta funktion ln(1 + ex2y3z) 1. kertaluvun osittaisderivaatat kaikkien muuttujien suhteen.(b) Osoita, että funktio arctan
 toteuttaa Laplacen osittaisdifferentiaaliyhtälön
toteuttaa Laplacen osittaisdifferentiaaliyhtälön
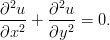
(Tällaisia funktioita sanotaan harmonisiksi funktioiksi.) Vihje: Laske ainakin joku käsin ja tarkista kaikki Maplella. Tällaiset mekaaniset, tarkkuutta vaativat tehtävät ovat onnen omiaan CAS-ohjelmille, kuten Maple, Mathematica. Maplen diff hoitelee homman.
- 7. mplV0015.tex
(Myös mplDi017.tex (poistetaan))
Oletetaan, että funktioilla u(x,y) ja v(x,y) on jatkuvat toiset osittaisderivaatat ja ne toteuttavat ns. Cauchy-Riemannin yhtälöt: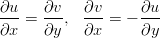
Osoita, että u ja v ovat harmonisia, eli toteuttavat Laplacen differentiaaliyhtälön:
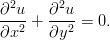
Mapletekniikkaa: b) Kirjoita CR-yhtälöt tyyliin
diff(u(x,y),x)=diff(v(x,y),y)
Maplen diff-operattorin täytyy tietää, että lauseke, johon derivointi kohdistuu, sisältää muuttujat x ja y. Muussa tapauksessa se räväyttää ilman muuta tuloksen 0 (nolla), joka on samalla tehtävän suorituksen arvo. Ratkaisu: mplVektori/mplV0015R.mw ja .pdf - 8. mplV0016.tex
Olkoon f(x,y) = x3y2 + x4 sin y + cos(xy). Laske osittaisderivaatat f xxy, fxyx, fyxx ja totea, että ne ovat samat.Voit antaa Maplen laskea.
- 9. mplV0017.tex
Laske yhdistetyn funktion derivoimissääntöä (eli ketjusääntöä, ”chain rule”) käyttäen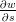 ja
ja 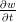 , kun
, kun
(a) w = x ln(x2 + y2), x = s + t,y = s − t ,
(b) w = ex+2y sin(2x − y), x = s2 + t2, y = 2s2 − t2Tee käsin ja tarkista Maplella.
- 10. mplV0018.tex
Kolmionmuotoisen maa-alan kahden sivun mitatut pituudet ovat 224 m ja 158 m ja niiden välinen kulma 64∘ . Pituusmittauksen virheraja on 0.4 m ja kulman 2∘ . Mikä on pinta-alan likimääräinen suhteellinen maksimivirhe.Vast: n. 2 %
- 11. mplV0019.tex
Osittaisderivoituvan funktion f : ℝ2 → ℝ gradientti ∇f määritellään näin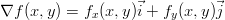
Olkoon f(x,y) = |xy| .
(a) Piirrä tasa-arvokäyrät(korkeuskäyrät) f(x,y) = k,k = 1, 2, 3.
(b) Piirrä f:n gradienttikenttävektoreita fieldplot:n avulla samaan kuvaan korkeuskäyräpiirrosten kanssa. Kun käytät samaa skaalaa akseleilla pitäisi kuvasta näkyä, miten gradienttivektorin ja korkeuskäyrän suunnat suhtautuvat toisiinsa.
Vihje: Gradientti voidaan ladata useastakin kirjastosta. Selvintä on määritellä itse:
gradi2:=(f,x,y)->[diff(f,x),diff(f,y)]
(Voit myös ladata: with(linalg); ja saat käyttöön funktion grad)with(plots) lataa contourplot- ja fieldplot-funktiot.
Grafiikkojen yhdistäminen:kuva1:=contourplot(...)
kuva2:=fieldplot(...)
display(kuva1,kuva2); - 12. mplV00191.tex
Työarkilla ../MattieT/mplteht/ohjeet/pintoja.mw (ja .pdf) kohdassa ”toinen esimerkki” tarkastellaan funktiota f(x,y) =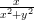 . Sekä plot3d- että contourplot-kuvat
ovat lievästi sanoen harhaisia. (Toki erilaisilla optioilla voi plot3d-kuvaa olennaisesti
parantaa.) Selvitä, minkälainen kuvaaja todellisuudessa on. Tarvitset taas
sekä Maplea että kynää ja paperia. Piirtele myös pystyleikkauksia, oikeita
korkeuskäyriä ym. ***
. Sekä plot3d- että contourplot-kuvat
ovat lievästi sanoen harhaisia. (Toki erilaisilla optioilla voi plot3d-kuvaa olennaisesti
parantaa.) Selvitä, minkälainen kuvaaja todellisuudessa on. Tarvitset taas
sekä Maplea että kynää ja paperia. Piirtele myös pystyleikkauksia, oikeita
korkeuskäyriä ym. ***
Hm, tämä on parasta muuttaa tehtäväksi (tai esimerkiksi), ratkaisu on suoraan tuolla, ja uudemmat versiot ovat poistaneet harhat.
*** Vihje: Usein pintapiirrosta voidaan täsmentää ja tarkentaa ja ymmärtää paremmin, kun piirretään sopivia avaruuskäyriä pinnalle spacecurve:lla.
Alla on esimerkki (sama kuin alussa ohjetiedostossa mplV000.tex), jossa piirretään napasädettä pitkin kulkevan pystytason ja annetun pinnan leikkauskäyrä sekä käyrän projektio xy-tasossa. Varsin käyttökelpoinen tapa monessa yhteydessä. Tätä voi modifioida tarpeen mukaan.
with(plots):
f:=(x,y)->4-x^2-y^2;
x:=r*cos(Theta):y:=r*sin(Theta): Theta:=Pi/4:
pystyleikkaus:=spacecurve(–[x,y,f(x,y)],[x,y,0]˝,r=0..2,thickness=3,
color=blue,axes=BOX)
# HUOM! html:ssa edellinen nakyy vaarin, pitaa olla:
# pystyleikkaus:=spacecurve(Aaltoauki[x,y,f(x,y)],[x,y,0]Aaltokii,r=0..2,...)
# missa Aalto tarkoittaa aaltosulkua,
x:=’x’:y:=’y’: # Kannattaa muistaa vapauttaa.
pinta:=plot3d(f(x,y),x=-2..2,y=-2..2):
display([pinta,pystyleikkaus],style=patchcontour,transparency=0.5);
display(pystyleikkaus); # Katsotaan pelkkaa leikkauskayraa. - 13. mplV00192.tex
Maaston korkeus (merenpinnasta mitattuna) karttakoordinaattien funktiona olkoon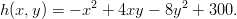
- Kulkuri K ottaa pisteestä (1, 2,h(1, 2)) lähtöaskeleen kaakkoon. Nouseeko
hän vai laskeutuuko?
Tämä on käsinlaskutehtävä, mutta tee Maplella. Havainnollista Maplepiirroksin:
Pintapiirros: plot3d, korkeuskäyrät: contourplot tai implicitplot. Leikkauskäyrä kaakko-luode-suuntaisen pystytason kanssa. - Muodosta funktion h(x,y) gradienttifunktio (gradienttikenttä). Piirrä gradienttikenttä plots-pakkauksen funktiolla fieldplot. Yhdistä korkeuskäyräpiirros tämän kanssa display-funktion avulla.
Vihje: Gradienttikentän voi laskea (tietysti käsin) tai derivoimalla Maplen diff:llä tai linalg-pakkauksen funktiolla grad. Ei ole pahitteeksi, jos kokeilet kaikkia tapoja.
- Kulkuri K ottaa pisteestä (1, 2,h(1, 2)) lähtöaskeleen kaakkoon. Nouseeko
hän vai laskeutuuko?
- 14. mplDi0019a.tex
Osittaisderivoituvan funktion f : ℝ2 → ℝ gradientti ∇f määritellään näin ∇f(x,y) = fx(x,y)i + fy(x,y)j .Olkoon f(x,y) = |xy| .
(a) Piirrä tasa-arvokäyrät(korkeuskäyrät) f(x,y) = k,k = 1, 2, 3.
(b) Piirrä f:n gradienttivektoreita ∇f(x,y) tasa-arvokäyrien pisteisiin. Kun käytät samaa skaalaa akseleilla (scaling=constrained), pitäisi kuvasta näkyä, miten gradienttivektorin ja korkeuskäyrän suunnat suhtautuvat toisiinsa.Vihje:
Aloita työarkki näin:
> restart:
> with(plots): with(plottools):
> nuoli:=(alkup, loppup,vari)->arrow(alkup,loppup,0.01,0.05,0.02,color=vari);
> korkeuskayra:=k->implicitplot(abs(x*y)=k,x=-2..2,y=-2..2);
> # Maariteltiin grafiikka-arvoinen funktio, usein tosi katevaa!
> kkparvi:=display(seq(korkeuskayra(k),k=1..3);
>Kts. lisää: mplDi0002Apu.mw
- 15. mplV003.tex
Piirrä avaruuskäyrä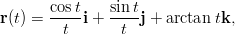
kun t ∈ [1,T] ja T = 100. Määritä käyrän kaarenpituus ja tutki, onko sillä raja-arvoa, kun T →∞. Vihje: Käyrä on luontevinta kirjoittaa listaksi r = [cos(t)/t,sin(t)/t,arctan(t)] ja laskea kaarenpituus integraalista ∫ |r′(t)|dt.
- 16. Määritä funktion f(x,y) = x2 − y suurin arvo ympyrällä x2 + y2 = 1. Käytä Lagrangen menetelmää. Vihje: (diff, solve, f:= (x,y)->(x2+y). Jos et ehdottomasti osaa Lagrangen menetelmää, lataa with(Student[MultivariateCalculus]) ja tutki LagrangeMultipliers-dokumentaatiota.
- 17. mplV006.tex
Lausu neliömuodon q(x) = xT Ax definiittisyydet symmetrisen matriisin A ominaisarvojen (merkkien) avulla.(Määritelmä paperin lopussa (tai kokoelman alussa).) Vihje: Lausu neliömuoto pääakselikoordinaattien yi avulla, sitten voit lukea kuin avointa kirjaa.
(Puhdas päättelytehtävä, “tietokonevapaa”.) - 18. mplV006a.tex
(Puhdas päättelytehtävä, “tietokonevapaa”.)
Osoita 2 × 2 symmetrisen matriisin A tapauksessa, että matriisi on- definiitti (pos. tai neg.), jos ja vain jos det(A) > 0 ,
- indefiniitti, jos ja vain jos det(A) < 0 ,
- semidefiniitti, jos ja vain jos det(A) = 0
![[ a c ]
c b](mapleHarVektori16x.png) ja muodosta karakteristinen polynomi. Käytä hyväksesi toisen
asteen yhtälön juurien ominaisuuksia. (Jos et muista, niin kerro auki (λ − λ1)(λ − λ2).)
Ratkaisu: mplV006aR.pdf ja .mw (html:ssa ratkaisu-linkki)
ja muodosta karakteristinen polynomi. Käytä hyväksesi toisen
asteen yhtälön juurien ominaisuuksia. (Jos et muista, niin kerro auki (λ − λ1)(λ − λ2).)
Ratkaisu: mplV006aR.pdf ja .mw (html:ssa ratkaisu-linkki)
- 19. mplV006b.tex
Määritä seuraavien neliömuotojen matriisit sekä definiittisyys:(a) q(x1,x2) = 2x12 + 4x 22 + x 1x2
(b) q(x1,x2,x3) = x32 + 2x 1x3 + 2x2x3
(c) q(x1,x2,x3,x4) = x12 + 2x 42 − 4x 2x3Esitä neliömuodot pääakselikoordinaateissa. Ei ole pahitteeksi, vaikka piirrät joitakin kuvia. Vihje: Avainsanat: 1neliomuoto,1pos1neg1definiitti, 1paaakseliprobleema, 1principalaxes,1ominaisarvot,1eigenvalues,1mplVektori
- 20. mplV006c.tex
Mitä kartioleikkausta edustaa yhtälö x12 + 24x 1x2 − 6x22 = 5Muunna yhtälö pääakselimuotoon ja piirrä kuva. (Voit ottaa mallia KRE Exa 6 s. 396 ”Transformation to principal axes”.)
tai GRE 11.6 s. 589 Voit myös katsoa: http://www.math.hut.fi/teaching/y3/harj/tyo/heigen.html
Muista: Hyperbelin luonteva parametriesitys on x = a cosh t, y = b sinh t
Maple-ohjeita: harj6ohje.mws -TODO!- Vihje: Avainsanat: 1neliomuoto,1pos1neg1definiitti, 1paaakseliprobleema, 1principalaxes,1ominaisarvot,1eigenvalues,1mplVektori
- 21. TV-yhtiö on (pahaa aavistamatta) palkannut matemaatikon seikkailukilpailun juontajaksi. Kilpailussa tehtävänä on kiertää mahdollisimman lyhyt reitti sen kolmion sisällä, jonka kärjet ovat pisteissä (0, 0), (2, 0) ja (0, 2). Lähtö tapahtuu pisteestä (1, 0), ja kilpailijan tarvitsee koskettaa jokaista muuta kolmion sivua ja palata sitten alkupisteeseen Määritä lyhin tällainen reitti, ja sen pituus. Vihje: Muodosta matkan funktio f(x,y) – mieti ensin, mitä kuvaa x ja mitä y, ja sen jälkeen, kuinka etäisyys laskettaisiin (vihje: Euklidinen etäisyys). Tämän jälkeen etsi funktion f kriittiset pisteet, eli osittaisderivaattojen nollakohdat, ja tutki niiden laatua. Valitse näistä pisteistä minimin tuottava, ja laske pituus.
- 22. mplV010.tex
Määritä funktion f(x,y) =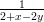 astetta 2 oleva Taylorin polynomi kehitettynä
pisteessä (2, 1) Tee 2. asteen polynomi ensin käsin ja sitten Maplella. Kts. myös
ohjetiedostoa (tulee).
astetta 2 oleva Taylorin polynomi kehitettynä
pisteessä (2, 1) Tee 2. asteen polynomi ensin käsin ja sitten Maplella. Kts. myös
ohjetiedostoa (tulee).
Avainsanat: Usean muuttujan Taylorin polynomi, diff, D, perushelppo . Ratkaisut tehtäviin mplV010 ja mplV011: “ratkaisut”-linkistä (molemmat samassa työarkissa).
- 23. mplV011.tex
- Muodosta funktion f(x,y) = cos(x + sin y) toisen asteen Taylorin polynomi kehitettynä (0, 0):ssa. Miten hyvän approksimaaton saat arvolle f(0.1,−0.2) ? (Vertaa laskimen tai Maplen antamaan arvoon, ei tarvitse miettiä jäännöstermiarviota.)
- Määritä funktion f(x,y) =
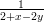 asteita 2,3 ja 4 olevat Taylorin
polynomit kehitettynä pisteessä (2, 1)
asteita 2,3 ja 4 olevat Taylorin
polynomit kehitettynä pisteessä (2, 1)
- Piirrä funktio f(x,y) ja eriasteisia Taylorin polynomeja pintapiirrokisna ja/tai korkeuskäyrinä.
Kts. myös harj7ohje.mws
Avainsanat: Usean muuttujan Taylorin polynomi, diff, mtaylor,plot3d,contour. Vihje: a)-kohta on käsinlasku, tarkistukseen siinäkin Maplen diff. b)-kohta Maplen diff -funktiolla. Lopuksi voit kokeilla myös mtaylor-komentoa. (Tarkoitus on Maple-avusteinen oppiminen, ei liian valmiiden “nappuloiden” paineleminen.) Ratkaisut tehtäviin mplV010 ja mplV011: “ratkaisut”-linkistä (molemmat samassa työarkissa).
- 24. mplV012.tex
Määritä funktion f(x,y) = x3 + y3 − 3xy kriittiset pisteet (KRP) ja niiden luonne. (min/max/satula/singulaari) Havainnollista piirroksin.Avainsanat: Kriittiset pistet, min/max, osittaiderivaatta, nollakohta. Vihje: Yhtälösysteemin ratkaisu: solve(–yht1,yht2˝,–x,y˝); Polynomiyhtälöissä kannattaa usein jatkaa komennolla allvalues. Numeerinen ratkaisu: fsolve
- 25. mplV013.tex
Määritä funktion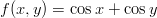
kriittiset pisteet (KRP) ja niiden luonne. (min/max/satula/singulaari) Havainnollista piirroksin.
Avainsanat: Kriittiset pisteet, min/max, osittaiderivaatta, nollakohta. Vihje: Yhtälösysteemin ratkaisu: solve(–yht1,yht2˝,–x,y˝);
- 26. DOKU mplV013a.tex
Määritä funktion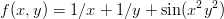
Maplen lisäksi kannattaa kokeilla Matlab:lla meshgrid, max/min, find ...-tekniikkaa. Toki ihan optimointiin räätälöityjä funktioitakin kummallakin ohjelmalla. Mutta ensisijaisesti ihan perustekniikoita, please!. (Osoittautuu sitäpaitsi, että minimize-tyyppiset “mustat laatikot” eivät oikein pärjää joka kohdassa.)
Jatkotehtävä: Määritä kaikki kriittiset pisteet yo. alueessa ja niiden luonne (max/min/satula).
Vihje: Vaatimattomasta ulkoasustaan huolimatta voi olla hiukan työläs, mutta sitäkin opettavaisempi.
Jatkotehtävässä esiintyy ehkä yllättävääkin käytöstä. - 27. mplV014.tex
Joudut tekemään vastuunalaisen päätöksen mitoista valmistettaessa laatikkoa. Pohjamateriaali on kaksi kertaa niin kallista pinta-alayksikköä kohti kuin sivu- tai kansimateriaali. Millä mitoilla saat V-tilavuuksisen laatikon materiaalikustannukset minimoiduksi? Perustele, että ratkaisusi on globaali minimi joukossa {(x,y)|x > 0,y > 0}. (Toisia derivaattoja ei välttmättä tarvita.)Avainsanat: minimointi,optimointi, osittaiderivaatta, nollakohta. Vihje: Sopii puhtaasti käsinlaskuun, toki saa käyttää Maplea laskuapualaisena.
- 28. mplV016.tex
Määritä funktion f(x,y) = x3 + y3 − 3xy kriittiset pisteet (KRP) ja niiden luonne. (min/max/satula/singulaari) Havainnollista piirroksin.Avainsanat: Kriittiset pisteet, min/max, osittaiderivaatta, nollakohta. Vihje: Yhtälösysteemin ratkaisu: solve(–yht1,yht2˝,–x,y˝); Polynomiyhtälöissä kannattaa usein jatkaa komennolla allvalues. Numeerinen ratkaisu: fsolve
- 29. mplV017.tex
- Olkoon f(x,y) =
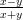 .
.
Määritä pinnan z = f(x,y) tangenttitaso pisteessä (2,−1). Piirrä pinta ja tangenttitaso ja pyörittele ja zoomaa. - Sama pinnalle z = arctan
 pisteessä (2, 2,π∕4).
pisteessä (2, 2,π∕4).
Vihje: (Kts. ..H/harj6ohje.mws) -TODO-
Avainsanat: 1mplVektori,1tangenttitaso,1tangent1plane,1several1variables - Olkoon f(x,y) =
- 30. mplV018.tex
Määritä lieriöiden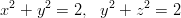
leikkauskäyrän pisteen (1,−1, 1) kautta kulkevan tangentin yhtälö.
Lieriöpinnan piirtäminen sujuu hyvin plot3d:llä. Kannttaa ajatella lieriö (kahdesta parametristä riippuvana) parametrimuotoisena pintana. Ensimmäisen lieriön luonnollinen parametriesitys on x =
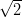 cos t,y =
cos t,y = 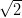 sin t,z = z. Tässä siis t ja z ovat
parametreja.
sin t,z = z. Tässä siis t ja z ovat
parametreja.
Edellinen voisi näyttää tältä:
plot3d([sqrt(2)*cos(t),sqrt(2)*sin(t),z],t=0..2*Pi,z=c..d);
Jälkimmäinen vastaavasti. Kuvat yhdistetään:
display(kuva1,kuva2);
Huom! plot3d on monipuolinen funktio, sille voi antaa pinnan muodossa f(x,y), mutta myös parametrimuodossa yllä kaavailtuun tapaan.
- 31. Määritä funktion f(x,y) = x2 − y suurin arvo ympyrällä x2 + y2 = 1. Käytä Lagrangen menetelmää. Vihje: (diff, solve, f:= (x,y)->(x2+y). Jos et ehdottomasti osaa Lagrangen menetelmää, lataa with(Student[MultivariateCalculus]) ja tutki LagrangeMultipliers-dokumentaatiota.
