
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Maple harjoitustehtäviä liittyen lineaarialgebraan ja matriisien kanssa toimimiseen Maplessa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. Tiedosto: mplP001.tex
Ohjelmat: Maple, [Mathematica]Sievennä lauseke
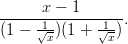
Vihje: Kokeile funktiota simplify.
- 2. mplP002.tex (PA P1 s.2011)
- 1.
- Klikkaa hiirellä (Viikkoharjoitukset-sivun) tiedostoa (maple1.mw) tässä mplP002Pohja.mw ja avaa se ohjelmalla Maple 15. Käy läpi työarkin tehtävät ja siirry sen jälkeen alla oleviin tehtäviin.
- 2.
- a) Kokeile Maplen voimia seuraavien sarjojen kohdalla:
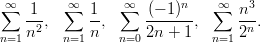
b) Montako termiä hajaantuvasta sarjasta
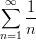
on otettava mukaan, jotta vastaava osasumma olisi vähintään 100?
(sum, evalf, infinity)
Vihje:
- 3. mplP002a.tex (PA P1 s.2011)
Fibonaccin lukujono (fn) määritellään alkuehdoilla f0 = 0, f1 = 1 ja palautuskaavalla fn+2 = fn + fn+1, kun n ≥ 2. Samat luvut saadaan suoraan lausekkeesta
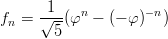
arvolla φ =
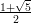 . Määrittele fn = f(n) funktiona ja osoita, että sekä alkuehdot
että palautuskaava toteutuvat.
. Määrittele fn = f(n) funktiona ja osoita, että sekä alkuehdot
että palautuskaava toteutuvat.
Vihje: Määrittele aluksi phi:= ... Palautuskaavan kohdalla on helpompi osoittaa jokin lauseke nollaksi kuin verrata kahta hankalaa lauseketta.
(sqrt, simplify, expand)Vihje: Muista funktiomääritys:
f:=n->... - 4. mplP002b.tex (PA P1 s.2011)
Intialaisen matemaatikon Srinivasa Ramanujanin (1887–1920) keksimän kaavan mukaan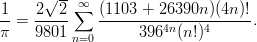
Tutki (numeerisesti), monennenko osasumman avulla saadaan luvun 1∕π likiarvo 50 desimaalin tarkkuudella.
b) Määrittele sarjan yleinen termi an = a(n) funktiona ja laske raja-arvo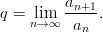
Sarja suppenee siis suunnilleen samaa vauhtia kuin sellainen geometrinen sarja, jonka suhdeluku on q.
(Pi, sqrt, sum, evalf(luku, desimaalien lkm), limit)Vihje: Muista funktiomääritys:
a:=n-> ... - 5. Suorita Maplella :> series(exp(x), x = 0, 10); # tai taylor(…);
> p:=convert(%,polynom);
> c:=coeffs(p,x);
> evalf(%);Selitä, mitä näissä tapahtuu. (Tutki tarvitessasi helpillä tyyliin ?convert.)
Piirrä polynomin p kuvaaja sopivalla välillä.
- 6. Etsi lukujen 12343243 ja 7681 suurin yhteinen tekijä.
Vihje: Suurin yhteinen tekijä lasketaan funktiolla igcd. Jos myös kertoimet halutaan tietää, kannattaa käyttää funktioita igcdex.
Luokittelu, avainsanat: Mapleperusteet, mplPerusteet, syt, gcd, lukuteoriaa
- 7. mplP006.tex (HA:n Maple-kirja ss. 48-50)
- 1.
- Laske 2123,π3,e5 neljälläkymmenellä (40) numerolla.
- 2.
- Mikä rationaaliluvuista
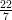 ,
,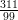 ,
,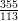 approksimoi parhaiten π:tä ?
approksimoi parhaiten π:tä ?
- 3.
- Kumpi luvuista πe , eπ on suurempi?
- 4.
- Jaa tekijöihin polynomi x3 − y3
Vihje:
?evalf
?factor - 8. mplP007.tex (HA:n Maple-kirja ss. 48-50)
Määrittele polynomilauseke p = x3 − 4x2 + 3x + 2.
Määritä p:n juuret ja piirrä kuvaaja välillä, joka sisältää juuret. Määritä myös paikalliset ääriarvot.Vihje:
p:= ... (ei siis p = ... (kuten Matlabissa))
plot(p,x=a..b)
?plot
solve yrittaa tarkkaa analyyttista ratkaisua (vaikka onnistuisi, voi olla turhan mutkikas)
fsolve numeerinen ratkaisijaLuokittelu: Maple perusteet, lausekkeet, yhtälöt, nollakohdat, grafiikka
- 9. mplP008.tex (HA:n Maple-kirja ss. 48-50)
Piirrä samaan kuvaan x4 ja 2x ja selvitä, kuinka monessa pisteessä ne leikkaavat. Varmaan joudut piirtämään useita kuvia eri alueilta.
Suurimman juuren etsimisessä voi oikean alueen ehkä löytää nopeimmin tyyppiä seq([x^4,2^x],x=a..b); olevalla komennolla.
Tutki fsolve-komennon help-teksti ja määritä likiarvo suurimmalle juurelle.
Vihje: seq(f(x),x=a..b) toimii kokonaislukuaskelin.
Toki askel voidaan säätää halutuksi tähän tyyliin:jono:=seq(a+i*h,i=0..10);Luokittelu: Maple perusteet, jonot (seq), yhtälöt, nollakohdat, grafiikka
- 10. mplP009.tex (HA:n Maple-kirja ss. 48-50)
Mitä tekevät seuraavat Maple-komennot:> sum(i^2,i=1..10);
> ifactor(1998); # Maple-oppaan kirjoitusvuosi
> ifactor(2012); # Aikaa on kulunut.
> solve(–x+2*y=5,x^2+y^2=10˝,–x,y˝);
> solve([x+2*y = 5, x^2+y^2 = 10], [x, y])Vihje: Kaksi solve-komennon muotoa liityvät tietorakenteisiin. Edellinen käsittelee joukkoina, jälkimmäinen listoina. (Joukon alkioilla ei ole määrättyä järjestystä päinvastoin kuin listassa.)
Luokittelu, avainsanat: Mapleperusteet, yhtälöryhmä, joukko, lista, tekijöihin jako.
- 11. mplP010.tex
Muodosta funktion cos(x) sin(x) ensimmäinen ja toinen derivaatta ja piirrä kunkin kuvaaja sopivaksi katsomallasi välillä kenties mieluiten eri koordinaatistoihin.Vihje:
- 12. mplP011.tex (HA:n Maple-kirja ss. 48-50)
Funktiolausekkeen derivaatta muodostetaan diff-komennolla.
Määritä seuraavien funktioiden 1. ja 2. derivaatta ja sievennä tulokset simplify-komennolla.
6x3 + 3x2 − 2x + 1 ,
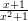 , cos(x2 + 1) , arcsin(2x + 3) ,
, cos(x2 + 1) , arcsin(2x + 3) , 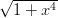 , arctan x
, arctan x
Luokittelu, avainsanat: Mapleperusteet, Maplediffint, lauseke, symbolinen derivointi, diff
- 13. mlP014.tex, mplP014.tex
Maple [Mathematica] , Matlab (erityisesti b)-kohta).
Tarkastellaan funktiota
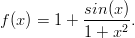
a) Maple: Määrittele f lausekkeeksi, laske f:n arvo pisteessä x = −2.0 ja piirrä kuvaaja välillä
![[− 5,5 ]](mapleHarPerusteet13x.png) .
.
Matlab:
Tee vastaava asia Matlabilla, kirjoita skripti. Huomaa, että Matlabissa täytyy ensin antaa x:lle numeerinen (vektori)arvo.b) Tee samat asiat, mutta nyt määrittelemällä f funktioksi.
Vihje:
a)
Maple Matlab:
> f:=1-... >> x=...
> subs... >> f=...
> plot >> plotb)
Maple Matlab
> f:=x->1-... >> f:=@(x) 1-...Ratkaisu: Ratkaisu:
mplPerusteet/mplP014R.mw ja .pdf
mlPerusteet/mlP014R.m ja .pdfLuokittelu:
mplteht/mplPerusteet/mplP014.tex, matlabteht/mlPerusteet/mlP014.tex
Avainsanat:
Mapleperusteet, funktiot, lausekkeet, Matlabperusteet
- 14. Laske funktion f(x) = e−x2 arvoja 0.5:n välein välillä 0…5, ja piirrä taulukoiduista arvoista kuvaaja
Vihje: Määrittele f funktioksi tyyliin f:=x-> ...
Muodosta jono seq-funktion avulla ja ympäröi se listasuluilla tyyliin: h:=0.5: x:=[seq(k*h),k=...]
Muodosta funktion arvot tyyliin y:=map(f,x)
Taulukon saat esim. array-funktiolla.
Datan voi piirtää nykyisin myös ”Matlab-tyylillä”: plot(x,y)Ratkaisu:
x := [seq(.5*k, k = 0 .. 10)]
f := x->exp(-x^2)
y := map(f, x)
array([x, y])
plot(x,y) - 15. Laske funktion f(x) = e−x2 arvoja 0.5:n välein välillä 0…5, ja piirrä taulukoiduista arvoista kuvaaja Vihje:
- 16. mplP017.tex [mplD019.tex]
Opiskelija ottaa lainaa 10000 euroa hetkellä k = 0 ja ryhtyy maksamaan sitä takaisin kuukauden päästä hetkellä k = 1. Kuukausikorko on 1% (huh!) ja takaisinmaksu tapahtuu kiintein maksuerin 450 EUR/kkOlkoon yk k:n kuukauden kuluttua jäljellä olevan velan määrä. Kirjoita differenssiyhtälö yk:lle.
Muodosta taulukko ja graafinen esitys, jossa on pisteet (k,yk), ja selvitä sen perusteella, miten kauan velan maksu kestää ja miten paljon rahaa opiskelijaparka käyttää koko projektiin.
Luokittelu: Maple-perusteet, Differenssi- ja differentiaaliyhtalot
Vihje:
