
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Maple harjoitustehtäviä liittyen lineaarialgebraan ja yhtälöryhmien ratkaisuun Maplessa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mplV000.tex
OhjeitaKerätään ohjeita näiden tehtävien aihepiiriin liittyen. “Tehtävä”-linkistä saat LATEX-koodin, josta sopivan osan voit haluamallasi tavalla muokaten liittää tehtäväpaperiisi.
Ominaisarvot ja -vektorit
Laskeminen
- Muodosta karakteristinen polynomi p(λ) = det(A − λI) ja määritä sen 0-kohdat, näin saat ominaisarvot.
- Ratkaise kutakin ominaisarvoa λ kohti lineaarinen yhtälösysteemi (A − λI)x = 0. Ratkaisu sisältää ainakin yhden vapaasti valittavan parametrin (muussa tapauksessa teit virheen λ:n laskennassa). Ratkaisuvektorit x ovat ominaisvektoreita. (Triviaalia nollavektoria ei kelpuuteta tähän kastiin.)
- “Oikeassa elämässä” ominaisvektorit lasketaan numeerisesti ja sitten ominaisarvot. Numeerinen laskenta on oma alansa, johon ei tässä paneuduta, vaan käytetään ohjelmistojen tarjoamia valmiita funktioita “mustina laatikkoina”.
Yleisiä ominaisominaisuuksia
- Kaksinkertaisen ominaisarvon tapauksessa voi olla yksi tai kaksi lineaarisesti riippumatonta ominaisvektoria.
- Eri ominaisarvoihin liittyvät ominaisvektorit ovat LRT.
- Symmetrisen matriisin ominaisarvot ovat reaaliset ja eri ominaisarvoihin liittyvät ominaisvektorit ovat ortogonaaliset.
Matriisin diagonalisointi
Jos n × n- matriisilla on n LRT ominaisvektoria, niin se on diagonalisoituva. Diagonalisointi (jos mahdollista) tarkoittaa matriisien X, D ja X−1 määrittämistä siten, että A = XDX−1 .
Käsin laskettaessa pitäisi osata kääntää 2 × 2-matriisi. Annetaan Maplen tehdä se yleisessä symbolisessa muodossa (ja generoida LATEX-muotoon), käytä hyväksesi:
A =
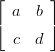
A−1 =
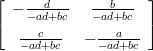
Lineaarikuvaus
Matriisi määrää lineaarikuvauksen (ja kääntäen). Tason tapauksessa siis 2 × 2-matriisi. Tehtävässä 6 on tarkoitus vain ottaa yleinen tason vektori (x,y), laskea sen kuva ao. matriisilla kerrottaessa, havainnollistaa piirroksella ja keksiä kuvaava nimitys.
Neliömuotojen definiittisyys
Määr: Neliömuoto q(x) = xT Ax (A on symmetrinen matriisi) on
- 1.
- positiivisesti definiitti, jos q(x) > 0 ∀x≠0,
- 2.
- negatiivisesti definiitti, jos q(x) < 0 ∀x≠0,
- 3.
- positiivisesti semidefiniitti, jos q(x) ≥ 0 ∀x ∈ ℝn ja ∃y≠0, jolla q(y) = 0,
- 4.
- negatiivisesti semidefiniitti, jos q(x) ≤ 0 ∀x ∈ ℝn ja ∃y≠0, jolla q(y) = 0,
- 5.
- indefiniitti, jos ∃x,y siten, että q(x) > 0 ja q(y) < 0.
Samoja definiittisyyskäsitteitä käytetään myös symmetrisestä matriisista A.
- 2. mplLi001.tex
Ratkaise yhtälöryhmä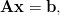
kun
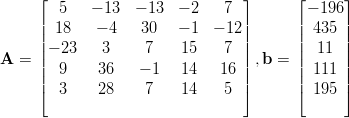
Vihje: Matriisin
![[a b c]
A = d e f](mapleHarLinis4x.png)
voi syöttää joko vaakavektoreita päällekkäin latomalla:
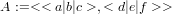
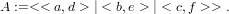
- 3. mplLi002.tex
Muodosta Maplessa matriisi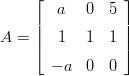
(a) Määrittele aliakset vihjeen mukaan.
(b) Muodosta karakteristinen polynomi suoraan määritelmän mukaan hyödyntäen aliaksia Det,Id.
(c) Muodosta karakteristinen polynomi LinearAlgebra-kirjaston CharacteristicMatrix ja Determinant-komentojen avulla.
(d) Sovella factor-komentoa polynomiin (sattuu onnistumaan), ja ratkaise puuttuvat juuret solve-komennolla.
e) Näppäise hiirellä matriisia A ja paina oikeaa painiketta. Valitse Eigenvalues, ja voit kokeilla muitakin.Vihje: Lataa kirjasto ja määrittele alias-nimet pitkille nimille:
> with(LinearAlgebra)
> alias(Det=Determinant,chmat=CharacteristicMatrix,Id=IdentityMatrix)
-
4.
mplLi003.tex
Tutustu tähän: http://www.math.hut.fi/teaching/v/3/02/L/LA.html, voit ottaa vastaavan .mws:n pohjaksi. Kirjoita viitteen http://www.math.hut.fi/teaching/v/3/00/L/G-J.html
Maple-työ LinaerAlgebra-tyylillä, LA.mws/html:n mallin mukaisesti. Tarkista rivioperaatiot ref- ja rref-aliaksia käyttäen. Selvitä ratkaisujen “lukumäärä” (olemassaolo ja mahd. vapaiden parametrien määrä). Tarkista lopuksi komennolla LinearSolve.Vihje: Maplessa on kaksi lineaarialgebrakirjastoa: vanhempi linalg ja uudempi LinearAlgebra. Tässä tehtävässä opetellaan uudemman käyttöä (se on mm. matriisien osien käsittelyn kannalta selkeämpää, selvästi Matlab-vaikutteista). Samalla opitaan/kerrataan oikeaa asiaa liittyen lineaaristen yhtälösysteemien perusoppiin.
-
5.
mplLi004.tex
Nyt emme enää harjoittele rivioperaatioilla laskemista, vaan kaikissa on lupa käyttää ref/rref-aliasoituja funktioita.Määritä kanta ℝ5:n aliavaruudelle, jonka virittävät vektorit v 1 = (1, 1, 0, 0, 1), v2 = (0, 2, 0, 1,−1), v3 = (0,−1, 1, 0, 2), v4 = (1, 4, 1, 2, 1), v5 = (0, 0, 2, 1, 3).
Jos Aatu saa tulokseksi jotkin vektorit ja Öhky saa jotkin toiset (saman määrän sentään toivottavasti), niin miten selvität, kumpi on oikeassa vai kenties kumpikin?
Vihje:
with(LinearAlgebra)
alias(ref=GaussianElimination,rref=ReducedRowEchelonForm)
- 6. mplLi005.tex
Olkoon A =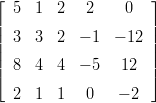 , ja merkitään sarakevektoreita a1,…,a5. Olkoon
B = [a1,a2,a4].
, ja merkitään sarakevektoreita a1,…,a5. Olkoon
B = [a1,a2,a4].
(a) Selvitä, miksi a3 ja a5 kuuluvat B:n sarakeavaruuteen col(B).
(b) Määritä nolla-avaruuden N(A) kanta.
(c) Olkoon T : ℝ5↦ℝ4 A:n määräämä lineaarikuvaus, ts. Tx = Ax (ts. T = L A). Selvitä, miksi T ei ole injektio eikä surjektio.Vihje:
with(LinearAlgebra)
alias(ref=GaussianElimination,rref=ReducedRowEchelonForm)
- 7. mplLi006.tex
Olkoon A =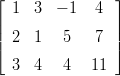
(a) Määritä sarakeavaruuden kanta.
(b) Määritä riviavaruuden kanta.
(c) Määritä nolla-avaruuden (ytimen) dimensio.
(d) Tarkista dimensioita koskevan peruslauseen toteutuminen.Vihje:
with(LinearAlgebra)
alias(ref=GaussianElimination,rref=ReducedRowEchelonForm)
- 8. mplLi007.tex
(a) Olkoon A m × n-matriisi ja Ab = [Ab] liitännäismatriisi. Lausu (välttämätön ja riittävä) ehto rangien r(A) ja r(Ab) avulla sille, että yhtälösysteemillä Ax = b olisi ratkaisu(ja) (eli on konsistentti).
(b) Osoita, että m × n-matriisille A pätee r(A) + n(AT ) = m
Vihje: Puhdas käsinlasku.
- 9. mplLi008.tex
(a) Osoita, että monomit 1,x,x2,…,xn ovat LRT ℝ:ssä. (b) Osoita, että ne ovat LRT myös jos määritelyjoukkona on mikä tahansa väli [a,b].
(Tietysti riittää tehdä pelkkä (b), niinhän.)
Tapoja on monia: (a)-kohdassa vektoriyhtälö voidaan derivoida toistuvasti ja laskea 0:ssa. Tai voidaan käyttää LRV-lemmaa ja todeta raja-arvokäytöksen perusteella, että xk ei voi yhtyä alemmanasteiseen polynomiin.
(b)-kohta hoituu ainakin polynomien tekijöihinjaolla (ei haittaa, vaikka tulee kompleksilukuja mukaan). Eräs tapa olisi osoittaa, että ns. Vandermonden matriisi on aina kääntyvä (sarakkeet LRT). (Toisaalta tämä tulee sivutuotteena, jos käytämme jotain muuta tapaa.) Kyseessä on matriisi, joka saadaan, kun monomit 1,x,…xn lasketaan n + 1:ssä pisteessä x 0,…,xn (Pisteet vaakasuuntaan, potenssit pystysuuntaan.) Maplen LinearAlgebra:ssa on VandermondeMatrix .
(c) Piirrä monomien kuvaajia vaikkapa välillä [−1, 1] ja yritä nähdä kuvasta lineaarinen riippumattomuus. Piirrä monomeja isoilla peräkkäisillä parillisilla (tai parittomilla) n:n arvoilla ja totea ”melkein LRV”. Tämä ilmenee numeerisessa laskennassa esim. interpolaatiopolynomin tapauksessa ”häiriöalttiutena”.
Vihje: Puhdas käsinlasku, paitsi c)-kohta.
- 10. mplLi009.tex
Matriisin N sarakkeet ovat koordinaatteja, jotka rajaavat ison N-kirjaimen.N =
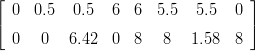
Piirrä ensin tuo N.
Sovella N:ään lineaarikuvausta, jonka matriisi on A =
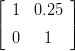 . Tämä on
tyyppiä ”leikkaus”, ”shear”. Piirrä tulos.
. Tämä on
tyyppiä ”leikkaus”, ”shear”. Piirrä tulos.
Skaalaa sen jälkeen x-koordinaatit kertomalla luvulla 0.75 ja piirrä taas.
Vapaaehtoinen lisäys. Pyörittele N:ää ”keskipisteen” ympäri siirtämällä keskipiste ensin O:oon ja kertomalla sopivalla kiertomatriisilla ja siirtämällä lopuksi takaisin.
Vihje: Ohje piirtoon: Nykyisin voidaan piirtää datapisteitä (yhdysjanoineen) Matlab-tyylisesti(kin) näin: > plot(v1,v2);
Matriisin M rivi k : M[k,1..-1]
(Vrt. Matlab: M(k,:))
Vanhempi tapa: Piirrettävä data pisteiden listana:
> convert(Transpose(N),listlist); plot(%); - 11. mplLi010.tex
(Kynä-paperitehtävä)
Tarkastellaan lämmönjohtumista ohuessa metallilevyssä. Oletetaan, että johtumista tapahtuu vain levyn suunnassa, ja levyn reunoilla on annetut (ajan suhteen) vakiolämpötilat. Levyn lämpötilat eri pisteissä asettuvat ajan kuluessa arvoihin, jotka ovat ajan suhteen vakioita, tällöin puhutaan lämpötilajakauman tasapainotilasta (”steady state”). Tehtävänä on määrittää lämpötilajakauma levyssä tasapainotilan vallitessa.Tarkastellaan kuvan mukaista tilannetta: (Klikkaa oikealla olevaa pdf-linkkiä, niin kuva näkyy kunnolla.)
--- 20----20---20----
— — — — —
10----*-----*-----*---40
— — — — —
10----*-----*-----*----40
— — — — —
----20----20----20---Kuvassa näkyvät annetut vakioreunalämpötilat (reunaehdot). Tehtävänä on laskea ratkaisuapproksimaatiot *:llä merkityissä sisäsolmupisteissä käyttäen seuraavaa periaatetta: Lämpötila levyn solmupisteessä on naapurisolmujen lämpötilojen keskiarvo.
Jos indeksoidaan solmupisteiden lämpötilat vaakarivijärjestyksessä: T1,…T6, voidaan ryhtyä kirjoittamaan yhtälöitä tyyliin:
T1 =
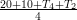 ,….
,….
Kirjoita koko 6 × 6- yhtälösysteemi ”standardimuodossa”.
Huom: Tasapainotilaratkaisu saadaan ns. Laplacen yhtälön ∇2T = 0 ratkaisuna. Tässä esitettyyn likimääräismenettelyyn ns. differenssimenetelmäänRatkaisua pyydetään seuraavassa tehtävässä.
- 12. mplLi011.tex
Ratkaise edellisen tehtävän yhtälösysteemi Maplea (tai Matlabia) käyttäen. (Tässä Maple-ohjeet.) Muodosta sitten edellisen tehtävän kuvan mukainen 4 × 5 matriisi, jossa on annetut reunalämpötilat sekä lasketut sisälämpötilat oikeilla kohdillaan. Ota nurkkapisteiden lämpötiloiksi kahden naapurisolmun lämpötilojen keskiarvo. Piirrä kuva, pyörittele hiirellä.Vihje: Tehtävässä riittää käytellä LinearAlgebra-kirjaston funktiota LinearSolve.
Ratkaisuvektorin muokkaaminen matriisiksi onnistuu mukavasti, kun leikkaat/liimaat alla olevan funktiomäärityksen Maple-työarkillasi. (Suorita leikkaus pdf-tehtävätiedostosta.)
Reshape:=(vek,m,n)->Matrix(linalg[matrix](m,n,convert(vek,list)));
Funktio on tehty vastaamaan Matlabin funktion reshape käytöstä siinä tapauksessa, jossa vektori muutetaan annetun kokoiseksi matriisiksi.
Lämpötilamatriisin rakentelu kannattaa hoidella (Matlabinomaiseen) tyyliin:
Tsisa:=Reshape(T,2,3); # vektorissa T on ratkaisulampotilat.
Tiso:=Matrix(4,5,0);
vaaka:=¡15—20—20—20—30>;
pysty:=...;
Tiso[2..3,2..4]:=Tsisa;
...Piirtäminen komennolla matrixplot (muista with(plots):)
matrixplot(Tiso,axes=boxed);
Pyörittele kuvaa hiirellä.
Huom: Sanomattakin on selvää, että tehtävä sopii erikoisen hyvin Matlab:lle. Tässä pikemminkin näytetään, että Maplen LinearAlgebra-työkaluilla voidaan matkia Matlab-työtapaa ja päästä lähelle samaa käsittelymukavuutta.
Lisätehtävä: Tee ratkaisu Matlabilla!
Palataan asiaan perusteellisemmin Matlab-tehtävien yhteydessä, jolloin käsitellään lähemmin differenssimenetelmää.
- 13. mplLi012.tex
Olkoon B = {1, cos t,…, cos 6t} ja C = {1, cos t,…, cos 6t}.Suorita Maple-komennot:
> cos(2*t): %=expand(%);
...
> cos(6*t): %=expand(%);Olkoon H = sp(B). Osoita, että B on H:n kanta. (Tämä on miltei pelkkä toteamus, sehän palautuu monomien LRT- ominaisuuteen.) Varsinainen tehtävä:
Kirjoita C:n vektorien B-koordinaattivektorit (käyttäen hyväksi edellä viitatun Maple-istunnon tuloksia) ja osoita niiden avulla, että C on LRT ja siis H:n kanta.
Vihje: Merkinnät kirjan Lay Linear Algebra mukaiset.
- 14. mplLi013.tex
Lay: Linear Algebra s. 277 teht. 17Olkoon B = {1, cos t,…, cos 6t} = {x 0,…,x6} ja C = {1, cos t,…, cos 6t} = {y0,…,y6}, kuten edellä (teht. mplLi012).
Edellä osoitettiin, että myös C on avaruuden H =sp{x0,…,x6} kanta.
(a) Muodosta P =
![[ ]
[y0]B | ... | [y6]B](mapleHarLinis13x.png) , ja laske P−1.
, ja laske P−1.
(b) Selitä, miksi P−1:n sarakkeet ovat vektorien x 0,…,x6 C-koordinaattivektoreita.
Kirjoita sitten trigonometrisiä kaavoja, joilla cos t:n potensseja voidaan lausua moninkertaisten kulmien kosinien avulla. Esimerkkinä sopivasta kaavasta olkoon: 5 cos 3t − 6 cos 4t + 5 cos 5t − 12 cos 6t.Tällainen esitysmuoto on mm. integroinnin kannalta erityisen hyödyllinen, kuten varmasti tiedät.
Vihje: Merkinnät kirjan Lay Linear Algebra mukaiset.
- 15. mplLi020.tex
Muodosta matriisin A =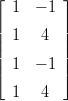 QR - hajotelma ja määritä sen avulla
PNS-ratkaisu yhtälölle Ax = b, missä b =
QR - hajotelma ja määritä sen avulla
PNS-ratkaisu yhtälölle Ax = b, missä b = ![[− 1,6,5,7]](mapleHarLinis15x.png) T
T
Mikä on PNS-virhe (“residuaali”) ||Ax − b|| ?
Kirjoita myös normaaliyhtälöt (mutta ei tarvitse ratkaista).
Vihje: Tämä on käsinlaskuksi tarkoitettu. Ainakin tarkistukseen ja ehkä välivaiheisiin sopii käyttää Maplea (Matlab-puolella - arvaa mitä!)
Huom: PNS-tehtäviä on myös hakemistoissa mlLinis, mplCurveFit mlCurveFit
- 16. Maple:
Muodosta Maplessa matriisi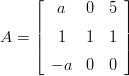
(a) Muodosta karakteristinen polynomi LinearAlgebra-kirjaston CharacteristicMatrix ja Determinant-komentojn avulla.
(b) Sovella factor-komentoa polynomiin (sattuu onnistumaan), ja ratkaise puuttuvat juuret solve-komennolla.
c) Näppäise hiirellä matriisia A ja paina oikeaa painiketta. Valitse Eigenvalues, ja voit kokeilla muitakin.Vihje:
- 17. mplLi030.tex
Laske matriisien A ja B ominaisarvot sekä B:n ominaisvektorit, kunA =
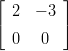 , B =
, B = 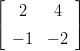
Voidaanko matriisien ominaisvektoreista muodostaa avaruuden ℝ2 kanta? (A-matriisin tapauksessa ei todellakaan tarvitse tätä johtopäätöstä varten laskea ominaisvektoreita.) Vihje: Käsinlasku/päättely Avainsanat: 1mplLinis,1ominaisarvot,1eigenvalues
- 18. mplLi031.tex
Matriisilla A =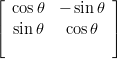 kertominen kiertää tason vektoreita kulmalla 𝜃.
Mieti ensin geometriselta kannalta, voiko tällä olla reaalisia ominaisarvoja
jollain/millään 𝜃:lla.
kertominen kiertää tason vektoreita kulmalla 𝜃.
Mieti ensin geometriselta kannalta, voiko tällä olla reaalisia ominaisarvoja
jollain/millään 𝜃:lla.
Laske sitten ominaisarvot ja -vektorit.
Vastaus laskutehtävään: Ominaisarvot: cos(𝜃) + i sin(𝜃), cos(𝜃) − i sin(𝜃) Ominaisvektorit: [1,−i], [1,i] Vihje: Käsinlasku/päättely, saa kokeilla myös Maple/Matlab/Mathematicalla Avainsanat: 1mplLinis,1ominaisarvot,1eigenvalues,1kiertokuvaus,1plane1rotation
- 19. mplLi032.tex
Muodosta matriisin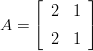
Käsinlasku/päättely, saa kokeilla myös Maple/Matlab/Mathematicalla Avainsanat: 1mplLinis,1ominaisarvot,1eigenvalues,1kiertokuvaus,1plane1rotation, 1matriisin1diagonalisointi, 1matrix1diagonalization
- 20. mplLi033.tex
Osoita, että vanha kunnon Fibonaccin jono (Fn) saadaan matriisin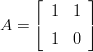
Diagonalisoi matriisi A, ja laske sen avulla kaava Fn:lle. Avainsanat: 1mplLinis,1ominaisarvot,1eigenvalues,1Fibonacci, 1matriisin1diagonalisointi, 1matrix1diagonalization
- 21. mplLi034.tex
Olkoon A =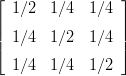
(a) Varmista, että näet päältäpäin, että ominaisvektoreista voidaan muodostaa ℝ3:n ortonormaali kanta.
(b) Laske ominaisarvot ja -vektorit Maplella käsinlaskutyyliä simuloiden (kts. L/ominaisarvot.mws), saat laskea käsinkin. Tarkista komennolla Eigenvectors (with(LinearAlgebra))
(c) Muodosta matriisin A ominaisvektoreista ortonormeerattu kanta ℝ3:lle. Eli muodosta matriisi X, jonka sarakkeina ovat normeeratut ominaisvektorit. Vihje: Tarkista ortonormaalisuus kertomalla XTX.
Tarkista, että diagonalisointi meni oikein kertomalla XTAX.Huom: Vektorin v euklidinen normi Maplella: norm(v,2); (Kts. myös ..L/ominaisarvot.mws) -TODO- Avainsanat: 1mplLinis,1ominaisarvot,1eigenvalues, 1matriisin1diagonalisointi, 1matrix1diagonalization, 1ortonormaai1ominaisvektorikanta, orthonormal1basisof1eigenvectors
- 22. mplLi035.tex
Spektri tarkoittaa ominaisarvojen joukkoa kompleksitasossa (n pistettä, joista osa saattaa yhtyä, spektraalisäde on r = max(|λj|) ja spektraaliympyrä siis r-säteinen ympyrä.) Spektri kertoo yleensä paljon matriisin luonteesta.Tehtävä Piirrä symmetristen, vinosymmetristen ja ortogonaalisten matriisien spektrejä. Lisää kuhunkin myös spektraaliympyrä.
Vihje: Jos A on mielivaltainen matriisi, niin sen avulla voit muodostaa symmetrisen matriisin esim: AT A tai A + AT , vinosymmetrisen AT − A Ortogonaalimatriiseja voit kehitellä vaikkapa soveltamalla GramSchmidt-funktiota satunnaismatriisin sarake (tai rivi)vektoreihin. Muista map.
Satunnaismatriisin tapauksessa toiminta voisi olla tämäntapaista:
> with(LinearAlgebra);
> z2xy:=z->[Re(z),Im(z)]; # Apufunktio, jolla muutetaan x+iy muotoon [x,y] .
> A:=RandomMatrix(20,20): # Hiiren oikea -> ‘‘browse’’ n”aytt”a”a alkiot.
> A:=convert(A,float); # Jotta siirryt numeeriseen menetelm”a”an...
> lam:=Eigenvalues(A); # ... ominaisarvojen laskennassa.
> plot(map(z2xy,[lam]),style=point,symbol=circle);
# Riisu vaikka ensin plot pois, niin n”aet piirrett”av”an rakenteen.Selvitä, vastaavatko kuvat odotuksiasi.
Avainsanat: 1mplLinis,1ominaisarvot,1eigenvalues,1spektri
- 23. mplLi036.tex
Viite: Lay s. 340 exa 8, s. 342 exe 27/28, vrt TE Huom 4.1 s. 44Olkoon T : ℝ4 → ℝ4 lineaarikuvaus, jonka matriisi luonnollisen kannan suhteen on
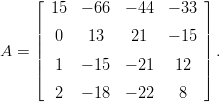
Määritä ℝ4:n kanta F, jonka suhteen T:n matriisi [T] F on diagonaalinen ja muodosta tuo diagonaalimatriisi.
Saat käyttää Eigenvectors:ia.
Avainsanat: 1mplLinis,1ominaisarvot,1eigenvalues,1matriisin1diagonalisointi, 1diagonalization
