
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Harjoitustehtäviä Maplen piirto-ominaisuuksien käyttöön.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. Tiedosto: mplG001.tex
Piirrä funktion f(x) = sin(8x) + sin(9x) kuvaaja.Vihje: Tarkastele riittävän pitkää väliä
- 2. mplG002.tex
- Suorita plot(1/x,x=-1..1); Miten saisit kuvan näyttämään paremmalta?
- Kokeile datan piirtoa tähän tapaan
h:=0.01: xy=seq([k*h,1/(k*h)],k=1..100);
plot([xy])(Data annettu xy-pisteiden listana.)
- ja myös:
x:=[seq(k*h,k=1..100)]: y:=map(z->1/z,x);
plot(x,y)(Matlab-tyylinen datan piirto (uusissa Maple-versioissa.))
- Kokeile nyt sitä Matlab-piirtoa vertailuksi viimeksi mainittuun:
h=0.01; x=h:h:1;
plot(x,1./x)
Vihje: a)-kohtaan:
( ?plot,options ). Etsi options-luettelosta discont=true- kohta. Kokeile myös, mitä discont(1/x,x); vastaa. - 3. mplG009.tex
Kun suoritat komennon with(plots): saat käyttöösi mm. funktiot contourplot ja implicitplot.
Kokeile vaikkapa contourplot(x^2+y^2,x=-5..5,y=-5..5) ja
implicitplot(x^2+y^2=1,x=-1..1,y=-1..1)Piirrä funktion f(x,y) = y ln x + x ln y korkeuskäyriä pisteen (1, 1) ympäristössä. Piirrä erityisesti se, joka kulkee pisteen (1, 1) kautta.
Klikkaa hiirellä kuvaa ja etsi käyrältä piste, joka on lähellä pistettä (1, 1). Seuraa pisteen koordinaatteja työkalunauhan vasemmasta laatikosta.
- 4. [Matlab,Maple,Mathematica] (Vihjeet ja ratkaisut tässä vain Matlab/Maple.)
Piirrä pintakuva ja korkeuskäyräpiirros funktiosta
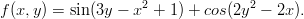
Ota alueeksi vaikka [-2 2 -1 1] .
Vihje:
1) Matlab
Käyttäjän täytyy itse muodostaa koordinaattihila ja sen pisteissä korkeusarvomatriisi Z. Tämä hoituu ”teho-operaattorilla” meshgrid, johon kannattaa panostaa muutenkin.
Korkeusarvomatriisi Z tehdään kahden muuttujan funktiolle tähän tapaan:x=linspace(a,b,m); y=linspace(c,d,n); % m ja n luokkaa 30.
[X,Y]=meshgrid(x,y);
Z=f(X,Y);(Kokeile periaatetta pienillä, hiukan erikokoisilla matriiseilla X,Y.)
Tässä funktion f on toimittava pisteittäisin operaatioin. Jos vaikka f(x,y) = x2 − y2, niin kirjoitettaisiin:Z=X.^2 - Y.^2;Pintoihin mesh(x,y,Z), surf(x,y,Z), ... Kokeile myös colorbar yms.
Matlabilla korkeuskäyriin contour , voit myös kokeilla ezcontour-funktiota. Mahdollisuus on kokeilla myös korkeuskäyrien valitsemistapoja, clabel.
Älä diskretoi liian hienoksi. Linspacessa 100 on ihan liikaa, n. luokkaa 30 olkoon lähtökohta.
2) Maple:
Helpompaa, koska hila tehdään ohjelman toimesta. Tulos ei aivan niin loistava kuin Matlabissa. (Osin tosin varsin hienoa tämäkin, ja “context sensitive”).with(plots):
plot3d(f(x,y),x=a..b,y=c..d);
contour(f(x,y),x=a..b,y=c..d); # Tarkista!Luokittelu:
mplteht/mplGrafiikka/mplGxx.tex, matlabteht/mlGrafiikka/mlGxx.tex
Avainsanat:
3D-grafiikka, pinta, pinnat, korkeuskäyrät, korkeuskayrat - 5. [Matlab,Maple,Mathematica] (Vihjeet ja ratkaisut tässä vain Matlab/Maple.)
Piirrä pintakuva ja korkeuskäyräpiirros funktiosta
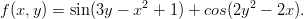
Ota alueeksi vaikka [-2 2 -1 1] .
Vihje:
1) Matlab
Käyttäjän täytyy itse muodostaa koordinaattihila ja sen pisteissä korkeusarvomatriisi Z. Tämä hoituu ”teho-operaattorilla” meshgrid, johon kannattaa panostaa muutenkin.
Korkeusarvomatriisi Z tehdään kahden muuttujan funktiolle tähän tapaan:x=linspace(a,b,m); y=linspace(c,d,n); % m ja n luokkaa 30.
[X,Y]=meshgrid(x,y);
Z=f(X,Y);(Kokeile periaatetta pienillä, hiukan erikokoisilla matriiseilla X,Y.)
Tässä funktion f on toimittava pisteittäisin operaatioin. Jos vaikka f(x,y) = x2 − y2, niin kirjoitettaisiin:Z=X.^2 - Y.^2;Pintoihin mesh(x,y,Z), surf(x,y,Z), ... Kokeile myös colorbar yms.
Matlabilla korkeuskäyriin contour , voit myös kokeilla ezcontour-funktiota. Mahdollisuus on kokeilla myös korkeuskäyrien valitsemistapoja, clabel.
Älä diskretoi liian hienoksi. Linspacessa 100 on ihan liikaa, n. luokkaa 30 olkoon lähtökohta.
2) Maple:
Helpompaa, koska hila tehdään ohjelman toimesta. Tulos ei aivan niin loistava kuin Matlabissa. (Osin tosin varsin hienoa tämäkin, ja “context sensitive”).with(plots):
plot3d(f(x,y),x=a..b,y=c..d);
contour(f(x,y),x=a..b,y=c..d); # Tarkista!Luokittelu:
mplteht/mplGrafiikka/mplGxx.tex, matlabteht/mlGrafiikka/mlGxx.tex
Avainsanat:
3D-grafiikka, pinta, pinnat, korkeuskäyrät, korkeuskayrat - 6. mplGxx.tex, mlGxx.tex (H2T6.tex )
Matlab,Maple,Mathematica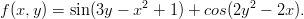
Piirrä pintakuva ja korkeuskäyräpiirros.
Ota alueeksi vaikka [-2 2 -1 1] .
Vihje: Tutustu samalla Matlabin meshgrid:n toimintaan.
Korkeusarvomatriisi Z tehdään kahden muuttujan funktiolle tähän tapaan:>> x=linspace(a,b,m); y=linspace(c,d,n); % m ja n luokkaa 30.
>> [X,Y]=meshgrid(x,y);
>> Z=f(X,Y);(Kokeile periaatetta pienillä, hiukan erikokoisilla matriiseilla X,Y.)
Tässä funktion f on toimittava pisteittäisin operaatioin. Jos vaikka f(x,y) = x2 −y2, kirjoitettaisiin: Z=X.^2 - Y.^2;Pintoihin mesh(x,y,Z), surf(x,y,Z), ... Kokeile myös colorbar yms.
Matlabilla korkeuskäyriin contour , voit myös kokeilla ezcontour-funktiota. Mahdollisuus on kokeilla myös korkeuskäyrien valitsemistapoja, clabel.
Älä diskretoi liian hienoksi. Linspacessa 100 on ihan liikaa, n. luokkaa 30 olkoon lähtökohta.
Maple: Helpompaa, mutta tulos ei aivan niin loistava kuin Matlabissa. (Osin tosin varsin hienoa tämäkin, ja “context sensitive”).
> with(plots):
> plot3d(f(x,y),x=a..b,y=c..d);
> contour(f(x,y),x=a..b,y=c..d); # Tarkista!Luokittelu:
mplteht/mplGrafiikka/mplGxx.tex, matlabteht/mlGrafiikka/mlGxx.tex
Avainsanat:
3D-grafiikka, pinta, pinnat, korkeuskäyrät, korkeuskayrat
