
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Harjoitustehtäviä liittyen differentiaali- ja integraalilaskentaan Maplessa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mplDi0001.tex Maple
Määritä funktion p(x) = x3 − 4x2 + 4x − 1 nollakohdat ja lokaali max/min. Piirrä funktion ja derivaatan kuvaajat.Vihje: solve,evalf,diff,plot. Yksinkertaisinta ehkä käsitellä lausekkeena, mutta saat kokeilla myös funktiotapaa.
- 2. mplDi0002.tex
Olkoon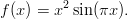
- Laske f′(4) käyttäen diff ja subs - komentoja. Laske tarkka arvo ja likiarvo. Muista: Pi edustaa vakiota π, pi edustaa vain vastaavaa kreikkalaista kirjainta ilman semantiikkaa.
- Sama D-operaattorin avulla.
- Miten voit a)-kohdassa muuttaa tuloksen derivaattafunktioksi?
- Määritä f′(4) erotusosamäärän raja-arvona.
Vihje: Komentoja: diff,D,subs,eval,evalf,limit
Funktiomääritykset: f:=x->lauseke(x)
(vrt. Matlab: f=@(x) lauseke(x))
Lausekkeen muuttaminen funktioksi “jälkikäteen”:
F:=unapply(lauseke(x),x
(lauseke(x) tarkoittaa lauseketta, jossa esiintyy symboli x.)
Huom! Uudet Maple-versiot (16 alkaen) armahtavat käyttäjää myös aiemmin ankarin kielloin varoitetusta funktiomäärityksen muodosta tyyliin:
f(x):=x*sin(x) Maple ystävällisesti kysyy, haluatko oikeasti määritellä funktioksi (ja 99%:ssa tapauksista vastaus on YES! (Uskallan sanoa.))Avainsanat: Maplediff, Mapleperusteet, lauseke/funktio
Vaikeusaste 1.
- 3. mplDi0002.tex
Olkoon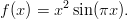
- Laske f′(4) käyttäen diff ja subs - komentoja
- Sama D-operaattorin avulla.
- Miten voit a)-kohdassa muuttaa tuloksen derivaattafunktioksi?
- Määritä f′(4) erotusosamäärän raja-arvona.
- 4. mplDi001.tex ([HAM] ss. 48-50)
Funktiolausekkeen derivaatta muodostetaan diff-komennolla.
Määritä seuraavien funktioiden 1. ja 2. derivaatta ja sievennä tulokset simplify-komennolla.6x3 + 3x2 − 2x + 1 ,
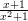 , cos(x2 + 1) , arcsin(2x + 3) ,
, cos(x2 + 1) , arcsin(2x + 3) , 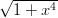 , arctan x
, arctan x
Vihje: Voit myös kirjoittaa lausekkeen työarkille, koskettaa sitä hiiren oikealla “context sensitive” näppäimellä, jolloin saat joukon Maple-komentoja, mm. diff, simplify ym.
Luokittelu, avainsanat: Mapleperusteet, Maplediffint, lauseke, symbolinen derivointi, diff
Viitteet:
[HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998.
- 5. mplDi0011.tex
Kuulantyönnön tulos riippuu kuulan alkunopeudesta v, lähtökorkeudesta h ja työnnön suuntakulmasta x seuraavan lausekkeen mukaisesti: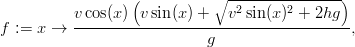
missä x ∈ [−π∕2,π∕2]. Käytetään SI-järjestelmän yksiköitä ja oletetaan, että h = 2, v = 14 ja g = 9.81. Määritä työnnön optimaalinen suuntakulma ja maksimitulos.
Kannattanee edetä seuraavien vaiheiden mukaan:
- Määrittele f funktiona; älä sijoita lukuarvoja tässä vaiheessa, niin voit tarkistaa, että lauseke on oikein.
- Sijoita lukuarvot h,v,g.
- Piirrä funktion f kuvaaja välillä −π∕2 ≤ x ≤ π∕2 ja tarkista, että se näyttää järkevältä. (Yleinen virhe: kertomerkkejä puuttuu!)
- Ratkaise maksimi kokeilemalla molempia tapoja: suoraan maximize TAI muodosta yhtälö f′(x) = 0, ratkaise numeerisesti fsolve-käskyllä, laske maksimi.
- Muuta saatu kulma asteiksi ja mieti, onko tulos järkevä.
- 6. mplDi002.tex
Olkoon f(x) = x2 − 4. Muodosta integraalifunktiot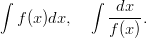
Tarkista tulokset derivoimalla.
Vihje: int ja Int. Voit myös aloittaa: int ¡ESC-näppäily>, saat valikon, josta valitset ∫ -merkin ja täydennät luonnollisen tapaan. Käytä simplify-komentoa tarvittaessa.
Luokittelu, Avainsanat: Maplediffint, int,Int,Mapleperusteet
.
- 7. mplDi003.tex
Määritä seuraavat integraalit:
Vihje: Ääretön: infinity. Huom: Voit kirjoittaa int(ESC), saat valikon, josta voit valita määrätyn integraalimerkin, rajojen paikalle kirjoitat sopivasti, ylärajan voit aloittaa infi(ESC), jolloin Maple antaa taas valikon, josta voit valita ∞-symbolin.
Toki voit kirjoittaa “vanhan hyvän ajan tapaan” int(f,t=0..infinity). - 8. mplDi004.tex
Huom! Alla jotkin kaavat html-sivulla epäselviä, suositus: avaa pdf-tiedosto (ellet jo avannut).Laske seuraavat integraalit. Määräämättömien integraalien tapauksessa tarkista tuloksesi derivoimalla. Määrätyissä integraaleissa, joista Maple ei suoriudu voit käyttää numeerista integrointia. Laske joitakin esimerkkejä (kuten h-kohta) “symbolisesti” ja sitten tulokselle numeerinen likiarvo ja toisaalta suoraan numeerisesti.
Huomaa, että ns. “suljettu muoto” on nykyisin epämääräinen käsite, sillä useat “perinteisesti mahdottomat” integraalit voidaan lausua Maple:n tuntemien erikoisfunktioiden (kuten erf ) avulla.
- a) ∫ 0π∕2 sin xdx b) ∫ x cos x2dx
- c) ∫
sin3x
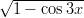 dx d)∫
ln xdx
dx d)∫
ln xdx
- e) ∫
x2
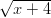 dx f) ∫
01
dx f) ∫
01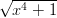 dx
dx
- g) ∫ 0πecos xdx h) ∫ −∞∞e−x2dx
Vihje: Integrointikomento on int. Lisäksi on komennon muoto Int, joka on ns. “hidas muoto” int:stä (“inert function”).
Numeerinen integrointi saadaan aikaan yhdistelmällä evalf(Int(...)) tai int(,...,numeric).
Muoto evalf(int(...)) yrittää ensin symbolista, ja evaluoi tuloksen. Jos symbolinen ei onnistu, integroi numeerisesti. Siksi saattaa olla paljon tehottomampi numeeriseen integrointiin.Avainsanat: mapleDiffint, symbolinen integrointi, numeerinen integrointi,erf
- 9. mplDi005.tex
Maple, Mathematica , Matlab (erityisesti b)-kohta).
Laske integraali
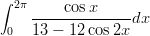
a) symbolisesti, b) numeerisesti. Piirrä integroitavan funktion kuvaaja. Mikä itse asiassa on integraalin arvo?
Vihje:
Mathematica:
Symbolinen integrointi tapahtuu funktiolla Integrate, numeerinen funktiolla
NIntegrate. Jälkimmäisessä sovelletaan suoraan jotakin numeerisen integroinnin menetelmää, jonka valintaan myös käyttäjä voi vaikuttaa. Ks. dokumentaatiota, erityisesti Implementation Notes.Maple:
Symbolinen integrointi tapahtuu funktiolla int, numeerinen funktiolla
int(...,type=numeric) tai evalf(Int(...)). Numeerisessa sovelletaan suoraan jotakin numeerisen integroinnin menetelmää, jonka valintaan myös käyttäjä voi vaikuttaa.
Esim: evalf(Int(f, x = 0 .. 2, digits = 20, method = ˙Dexp))Matlab:
Integrandi määritellään funktioksi (helpoimmin funktiokahvaksi “function handle”). Sitten quad-alkuiset Matlab-funktiot.Luokittelu:
mplteht/mplDiffint/mplDixx.tex, matlabteht/mlDiffint/mlDixx.tex
mmateht/mmaDiffint/mmaDi100
Avainsanat:
Symbolinen integrointi, numeerinen integrointi, funktiot, lausekkeet
Ratkaisu: ON (mplDi005R.mw, mplDi005R.pdf)
Viitteet:
http://math.tkk.fi/˜apiola/matlab/opas/lyhyt/m-files.html (Matlab:n funktiokahva, function handle)
.
- 10. mplDi005a.tex (PA, P1, tharj. 2, s. 2011)
Harjoituksessa käytetään Maple-ohjelmaa. Toisen harjoituksen tavoitteena on syventää tietoja funktioiden käsittelystä: aiheina ovat mm. derivointi, maksimointi, yhtälöiden ratkaiseminen (ja iterointi jos jää aikaa). Avaa Viikkoharjoitukset-sivulla oleva työarkki ja käy läpi siinä olevat esimerkit ja tehtävät. Sen jälkeen voit siirtyä alla oleviin tehtäviin, mikäli aikaa riittää.
- 1.
- Klikkaa hiirellä Viikkoharjoitukset-sivun tiedostoa maple2.mw
(tässä
http://www.math.hut.fi/opetus/Mattie/MattieT/mplteht/mplDiffint/mplDi005aPohja.mw), ja avaa se Maple-ohjelmalla. Käy läpi työarkin tehtävät ja siirry sen jälkeen alla oleviin tehtäviin. - 2.
- Putoavan kappaleen nopeus v = v(t) toteuttaa differentiaaliyhtälön
mv′(t) = mg−kv(t)2, jos positiivinen suunta on alaspäin ja ilmanvastus on
verrannollinen nopeuden neliöön kertoimella k > 0.
a) Osoita, että funktio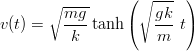
toteuttaa vaaditun differentiaaliyhtälön.
b) Mikä on rajanopeus lim t→∞v(t)?
Vihje: simplify-käsky ei tee sievennyksiä aivan loppuun, koska se ei tiedä, ovatko m,g,k positiivisia. Lisää käsky assume(m>0 and k>0 and g>0) ja kokeile sievennystä sen jälkeen. - 3.
- Kuulantyönnön tulos riippuu kuulan alkunopeudesta v, lähtökorkeudesta
h ja työnnön suuntakulmasta x seuraavan lausekkeen mukaisesti:
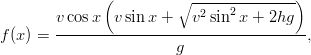
missä x ∈ [−π∕2,π∕2]. Käytetään SI-järjestelmän yksiköitä ja oletetaan, että h = 2, v = 14 ja g = 9.81. Määritä työnnön optimaalinen suuntakulma ja maksimitulos.
Kannattanee edetä seuraavien vaiheiden mukaan:
- Määrittele f funktiona; älä sijoita lukuarvoja tässä vaiheessa, niin voit tarkistaa, että lauseke on oikein.
- Sijoita lukuarvot h,v,g.
- Piirrä funktion f kuvaaja välillä −π∕2 ≤ x ≤ π∕2 ja tarkista, että se näyttää järkevältä. (Yleinen virhe: kertomerkkejä puuttuu!)
- Ratkaise maksimi kokeilemalla molempia tapoja: suoraan maximize TAI muodosta yhtälö f′(x) = 0, ratkaise numeerisesti fsolve-käskyllä, laske maksimi.
- Muuta saatu kulma asteiksi ja mieti, onko tulos järkevä.
Avainsanat: mplDiffint, PeruskurssiP1, putoavan kappaleen diffyhtalo, differentiaalyhtalo, yhtälö, simplify, assume
- 11. mplDi006.tex (Maple, Mathematica)
Laske integraali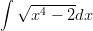
Yritä sieventää tulosta (äläkä masennu, kun ei sievene). Derivoi, sievennä ja hämmästy!
Vihje: Funktiot int (ja Int).
Tehtävä näyttää kovin viattomalta, mutta tulos voi yllättää ja lisätä kunnioitusta Maplen kykyihin. Samalla näkyy, että integroinnin ns. “suljettu muoto” on nykyohjelmissa huomattavasti laajentunut entisajoista.Luokittelu, avainsanat: MapleDiffint, integrointi, erikoisfunktiot
- 12. mplDi007.tex
[Isr] s. 46Ilmapallon tilavuus kasvaa nopeudella 10cm3∕s. Millä nopeudella säde kasvaa hetkellä, jolloin pallon pinta-ala on 200cm2?
Vihje: Periaate: V (t) =
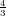 πr(t)3, A(t) = 4πr2. Derivoidaan: V ′(t) = lauseke, jossa esiintyy r(t) ja r′(t)
(implisiittinen derivointi). Tästä saadaan yksi yhtälö, josta voidaan ratkaista r′ V ′:n (tunnettu) ja
r:n avulla. r saadaan pinta-alaehdosta.
πr(t)3, A(t) = 4πr2. Derivoidaan: V ′(t) = lauseke, jossa esiintyy r(t) ja r′(t)
(implisiittinen derivointi). Tästä saadaan yksi yhtälö, josta voidaan ratkaista r′ V ′:n (tunnettu) ja
r:n avulla. r saadaan pinta-alaehdosta.
Voit aloittaa vaikka näin:
V:=(4/3)*Pi*r(t)^3; A:=4*Pi*r(t)^2;
yht1:=10=diff(V,t);yht2:=200=A;Huomaa, että diff soveltaa implisiittistä derivointia tuntemattomaan funktioon r(t).
Ratkaisu:
> V := (4/3)*Pi*r(t)^3;
> A := 4*Pi*r(t)^2;
> yht1 := 10 = diff(V, t);
> yht2 := 200 = A;
> r1 := solve(yht2, r(t));
> r1 := max(r1); # Valitaan pos.
> dr := solve(yht1, diff(r(t), t));
> subs(r(t) = r1, dr);Luokittelu, avainsanat: MapleDiffint, implisiittinen dervointi
Viitteet: [Isr] Robert Israel: Calculus: The Maple Way, Addison Wesley
- 13. mplDi008.tex
Missä pisteissä Cartesiuksen lehden x3 + y3 = 3xy tangentin suuntakulma jonkin koordinaattiakselin suhteen on = 45∘ ? Piirrä sekä käyrä että ko. tangentit (ainakin joku tangentti).Vihje: Implisiittinen derivointi ja numeerinen yhtälön ratkaisu fsolve lienevät paikallaan. Huomaa, että diff soveltaa implisiittistä derivointia tuntemattomaan funktioon y(x) (tai x(y)).
Luokittelu, avainsanat: MapleDiffint, implisiittinen derivointi, yhtälön numeerinen ratkaisu, fsolve
- 14. mplDi009.tex (Maple, Mathematica)
Muodosta funktion f(x) = arctan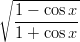 ensimmäinen ja toinen derivaatta. Piirrä
funktion ja derivaattojen kuvaajat.
ensimmäinen ja toinen derivaatta. Piirrä
funktion ja derivaattojen kuvaajat.
Vihje: Derivaatat ovat aluksi todella sotkuisia. Käytä komentoa simplify siistiäksesi tulostusta.
Kuvat saattavat yllättää ja johdatella pohtimaan, miksi?Ratkaisu:
(Poista kommentit ...)
%> f := x -> arctan(sqrt((1-cos(x))/(1+cos(x))))
%> plot(f(x),x=-2*Pi..2*Pi)
%> df := diff(f(x), x)
%> df:=simplify(df)
%> plot(df,x=-Pi..Pi)
%> d2f:=diff(df,x)
%> simplify(%)Luokittelu, avainsanat: diff, simplify, plot,diffint1, peruskurssi1
- 15. mplDi010.tex
Määritä funktion f(x) = arcsin(2x
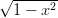 ) suurin ja pienin arvo välillä
[−1, 1].
) suurin ja pienin arvo välillä
[−1, 1].
Käytä symboliohjelmissa perinteistä “diffistekniikkaa” kuvan kanssa, Matlab:ssa raakaa “numeronmurskausta” tyyliin: linspace, plot, zoom, uusi linspace kapeammalla välillä, find, ...
Vihje: arcsin on Mathematicassa ArcSin, Maplessa arcsin ja Matlabissa asin.
Symbolilaskentaohjelma saattaa johtaa oikeaan tulokseen puutteellisin perustein, jos tarkkoja ollaan.Ratkaisu: Tämän kohdan ratkaisulinkissä Maple-ratkaisu, Matlab-ratkaisu vastaavassa Matlab-kohdassa (../../matlabteht/mlDiffint/mlDi010R.m ja .pdf)
Avainsanat: Diffint1,max/min, ääriarvot,peruskurssi1
- 16. mplDi011.tex
Ohjelmat: Maple,Mathematica
Laske sen alueen pinta-ala, jota rajoittavat käyrät y2 = x ja x − y = 3. Vihje: Mieti, kumpi on helpompaa: integrointi x- vai y-suunnassa. Ratkaisu: mplDi011.pdf (pdf-tiedosto),
mplDi011.mw (Maple ws)
...mmateht/mmaDiffint/mmaDi107R.nb (Mma-notebook)
Luokittelu:
mplteht/mplDiffint/mplDi011.tex, mmateht/mmaDiffint/mmaDi107.tex
Avainsanat:
Pinta-ala, integraali,diffintperusteet,peruskurssi1. - 17. mplDi012.tex
(Maple,Mathematica)
Määritä ellipsin 9x2 + 16y2 = 144 sisään piirretyn (akselien suuntaisen) suorakulmion maksimaalinen pinta-ala. Piirrä ellipsi ja suorakulmio.Ratkaisu: Maple: mplDiffint/mplDi012R.mw
mplDiffint/mplDi012R.pdfAvainsanat: Diffint1, ääriarvot, peruskurssi1,diffintperusteet
- 18. mplDi013.tex
(Mathematica,Maple)
Määritä funktion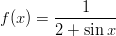
integraalifunktio ja piirrä sen kuvaaja. Onko tämä jatkuva? Pitäisikö sen olla jatkuva? Laske funktion integraali jakson [0, 2π] yli a) integroimalla analyyttisesti komennolla Integrate, b) integroimalla numeerisesti komennolla NIntegrate, c) muodostamalla ensin integraalifunktio komennolla Integrate ja sijoittamalla rajat tähän korvausoperaattoria käyttäen.
Vihje: Mathematica:
Komennolla Integrate lasketaan sekä integraalifunktio että määrätty integraali. Numeeriselle integroinnille (määrätyn integraalin laskemiseen) on komento NIntegrate. Korvausoperaattori on ReplaceAll eli /. .Maple: Integrointi: int, “hidastusmuoto”: Int.
Numeerinen integrointi: int(lauseke,x=a..b,numeric).
Arvon (a) sijoittaminen lausekkeen (F) muuttujaan (x): subs(x=a,F)Ratkaisu:
> f := 1/(2+sin(x)) # (Työarkilla matem. notaatio)
> F:=int(f,x)
> plot(F,x=0..2*Pi) # Oho, integroimisvakiot ei yhteensopivat.
> subs(x=2*Pi,F)-subs(x=0,F)
> simplify(%) # Ei voi olla, integroitava pos. koko välillä
> int(f,x=0..2*Pi)
> evalf(%)
> int(f,x=0..2*Pi,numeric) - 19. mplDi014.tex
(Mathematica,Maple)
Laske kardioidin r = 1 + cos φ kaarenpituus. Piirrä kuvio. Miten saat kardioidin kuvan oikeanmuotoiseksi? Tuntuuko saamasi pituus uskottavalta?Vihje: Kaarenpituusintegraali: ∫ ds = ∫
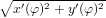 dφ.
dφ.
- 20. mplDi015.tex
Laske kaksinkertainen integraali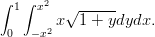
Laske tarkka arvo sekä likiarvo.
Vihje: Huom: Maplessa voit kirjoittaa integraalit, neliöjuuret ym. matemaattisena notaationa.
Tässä kaksoisintegraalissa syntyy jostain syystä oikeannäköisen matemaattisen kaavan kanssa vaikeaselkoinen virhe:
Error, unable to parse integral ... . Kyse on differentiaalitermin tulkintavaikeudesta.Perusnotaatio (int(int(...))) toimii varmasti.
Ratkaisu:
> int(int(x*sqrt(1+y), y = -x^2 .. x^2), x = 0 .. 1)
> evalf(%)Avainsanat: diffint2, kaksinkertainen integraali, peruskurssi2
- 21. mplDi016.tex
Osoita, että funktio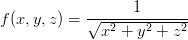
toteuttaa Laplace yhtälön fxx + fyy + fzz = 0.
Vihje: Laske osittaisderivaatat diff-komennolla. Tulos ei todennäköisesti suoraan anna nollaa, vaan kaipaa sieventämistä. Käytä tähän komentoa simplify.
Ratkaisu:
> f := 1/sqrt(x^2+y^2+z^2)
> diff(f, x, x)+diff(f, y, y)+diff(f, z, z)
> simplify(%)Avainsanat: diffint2, osittaisderivaatta, Laplacen yhtälö, peruskurssi2
- 22. mplDi017.tex
- Osoita, että funktio arctan
 toteuttaa Laplacen
osittaisdifferentiaaliyhtälön
toteuttaa Laplacen
osittaisdifferentiaaliyhtälön
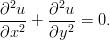
(Tällaisia funktioita sanotaan harmonisiksi funktioiksi.)
- Oletetaan, että funktioilla u(x,y) ja v(x,y) on jatkuvat toiset
osittaisderivaatat ja ne toteuttavat ns. Cauchy-Riemannin yhtälöt:
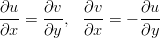
Osoita, että u ja v ovat harmonisia.
- Olkoon f(x,y) = x3y2 +x4 sin y +cos(xy). Laske osittaisderivaatat f xxy, fxyx, fyxx ja totea, että ne ovat samat.
Ratkaisu: mplDiffint/mplDi017R.mw ja .pdf
Avainsanat: Osittaisderivaatta, harmoniset funktiot, sekaderivaatat yhtyvät, diffint2, peruskurssi2
- Osoita, että funktio arctan
- 23. mplDi018.tex
Approksimoi numeerisesti kahden desimaalin tarkkuudella polun
![γ(t) = (cos(4πt),t2),t ∈ [0,1]](mapleHarDiffint24x.png)
pituutta. Idea on, että jaat välin [0, 1] n kappaleeseen tasapituisiä välejä, ja lasket näiden välien päätepisteitä vastaavien koordinaattien etäisyydet yhteen. Näin jakoa tihentämällä summan pitäisi lähestyä oikeaa pituutta. Muista, että saat tarkan pituuden laskemalla
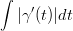
Vihje:
- 24. mplDi019.tex
Mat-1.1410 Matematiikan peruskurssi P1, syksy 2011, Pekka Alestalo
Harjoituksessa käytetään Maple-ohjelmaa. Viimeisen harjoituksen tavoitteena on tutustua integraalilaskentaan ja ratkaista siihen liittyvä sovellettu tehtävä. Lopuksi tutustutaan työarkin esimerkkien avulla jonojen, listojen ja matriisien käsittelyyn, jos jää aikaa.
Tarkista oman ryhmäsi aika ja paikka. Ota mukaasi (tämän paperin lisäksi) Viikkoharjoitukset-sivun Maple-pikaohje. Myös aikaisempien kierrosten malliratkaisut kannattaa kerrata.
- 1.
- Käy läpi edellisen kerran tehtävä 3 Noppa-sivun malliratkaisun avulla, ellet ehtinyt tehdä sitä viimeksi.
- 2.
- Klikkaa hiirellä Viikkoharjoitukset-sivun tiedostoa maple3.mw (puuttuu tästä toistaiseksi) ja avaa se ohjelmalla Maple 15. Käy läpi esimerkit ja laske annetut integraalit.
- 3.
- Työarkilla on annettu katenaariin eli ketjukäyrään liittyvä tehtävä,
jossa etsitään sellaisen köyden muotoa, jonka pituus on 6 ja jonka
päät on kiinnitetty pisteisiin (0, 1) ja (3, 2). Käy läpi esimerkkilaskut
väärästä yrityksestä paraabelin y = g(x) = Ax2 + Bx + C avulla ja
ratkaise sitten tehtävä oikean lausekkeen
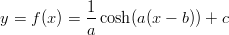
avulla. Ehdot tulevat siis muotoon f(0) = 1, f(3) = 2 ja
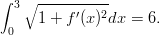
Piirrä lopuksi funktioiden f ja g kuvaajat samaan kuvaan ja vertaa tuloksia.
Hyödyllisiä vihjeitä:
- Kursoria ei tarvitse siirtää rivin loppuun ennen Enter-käskyä!
- Nuolinäppäimillä voi siirtyä yläindeksistä pois; samoin murtolausekkeissa.
- Pikanäppäimiä:
Ctrl + Delete poistaa käsky- tai tulosrivin
Ctrl + t siirtyy tekstitilaan
F5 siirtyy tekstitilassa kaavankirjoitustilaan ja takaisin
Ctrl + k tekee uuden käskyrivin kursorin yläpuolelle
Ctrl + j tekee uuden käskyrivin kursorin alapuolelle
Ctrl + l (l = label) liittää viittauksen aikaisemman tuloksen numeroon
Vihje:
- 25. mplDi020.tex
Integroi rationaalifunktiot: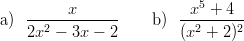
Saat käyttää Maplea apuna, mutta komennot convert(lauseke,parfrac,x) (puhumattakaan int :stä) ovat kiellettyjä muuhun kuin tarkistukseen. Katso mallia Maple-työskentelyyn vaikkapa /p/edu/mat-1.414/L2000/inttekn.mws:stä. Tehtävien ei pitäisi olla kohtuuttomia kokonaan käsinkään laskettaviksi.
** Linkki tuskin toimii, tee apu.zip ** Vihje:
Viitteitä: Tämä ja seuraavat n. 10 teht. kokoelmasta ... v2-3/H/harj2.tex (** Nootti systeemin rakentajalle(HA) **)
- 26. mplDi021.tex
Tynnyrin korkeus on h, pohjaympyrösöiden säteet a ja keskikohdalta otetun poikkileikkausympyrän säde b (a < b). Laske tynnyrin tilavuus, kun sivulaudat kaartuvat paraabelin muotoisesti.Vihje: Sopii käsinlaskuun ja Maple/Mathematica-harjoitteluun.
Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1
.
- 27. mplDi022.tex
Laske sen alueen pinta-ala, joka on ympyrän r = a sisäpuolella, mutta Bernoullin lemniskaatan r2 = 2a2 cos 2ϕ ulkopuolella. Vihje: Sopii käsinlaskuun ja Maple/Mathematica-harjoitteluun. Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1 - 28. mplDi023.tex
Laske asteroidin x = a cos 3t,y = a sin 3t koko pituus. Piirrä mielellään sekä Maplella (tai Mma:lla) että Matlabilla.Vihje: Sopii käsinlaskuun ja Maple/Mathematica(/Matlabkin)-harjoitteluun.
Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1
- 29. mplDi024.tex
Ketjukäyrän y = a cosh , |x|≤ a pyörähtäessä x-akselin ympäri syntyy
katenoidiksi kutsuttu pinta. Laske sen ala ja piirrä kuva (sopivalla a:lla).
Vihje: Sopii käsinlaskuun ja Maple/Mathematica(/Matlabkin)-harjoitteluun.
Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1
, |x|≤ a pyörähtäessä x-akselin ympäri syntyy
katenoidiksi kutsuttu pinta. Laske sen ala ja piirrä kuva (sopivalla a:lla).
Vihje: Sopii käsinlaskuun ja Maple/Mathematica(/Matlabkin)-harjoitteluun.
Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1 - 30. mplDi025.tex
Määritä ne p:n arvot, joilla seuraavat integraalit suppenevat ja määritä suppenevien integraalien arvot.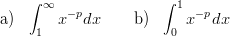
- 31. mplDi026.tex
Selvitä, suppeneeko ∫ 01 ln xdx. Integrointiin voit käyttää Maplen int-komentoa. Tarjoile ongelma Maplelle raja-arvona, johon sovellat limit-funktiota. Selvitä tuloksen oikeellisuus. Vihje: Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1 - 32. mplDi027.tex
Eulerin Γ-funktio määritellään kaavalla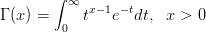
a) Osoita, että integraali suppenee aina kun x > 0.
b) Johda osittaisintegroimalla palautuskaava Γ(x):lle Γ(x − 1):n avulla ja osoita sitä käyttäen, että Γ(n + 1) = n!, kun n = 0, 1, 2,... .
c) Tutustu Gamma-funktioon piirtämällä Maplella tai Matlabilla. Huomaa, että Matlabissa ei ole (ollut) muuta tapaa n!:n laskemiseen kuin Gamman avulla. Pikku tarkennus (v. 2012): No, tokihan voi laskea: prod(1:n), mutta uudemmissa versioissa on myös factorial. Vihje: a)- ja b)-kohdat käsinlasku(pää-päättely)tehtäviä. Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1
- 33. mplDi028.tex (Maple,Matlab)
Selvitä, miksi seuraava Matlabin komentojono antaa exp-funktion (0:ssa muodostetun) Taylorin n-asteisen polynomin kertoimet.n=10,c=1:n,c=gamma(c+1),c=1./c,c=[1,c]
Huomaa, että kertoimet ovat kasvavan potenssin mukaan, joten jos/kun halutaan laskea polyval-funktiolla arvoja, on tehtävä y=polyval(fliplr(c),x);
a) Piirrä exp-funktio ja sen Taylorin polynomit Tk(x, 0), arvoilla k = 1…10 .
b) Suorita Maple-komento
seq(eval(subs(x=0,diff(exp(x),x$k) )),k=1..5); Se antaa varmasti idean, miten Maplen ja Matlabin yhteistyöllä voi kätevästi laskea minkä tahansa funktion Taylorin polynomeja x-vektorissa. Muodosta tällä tavoin joidenkin funktioiden Taylor-polynomitaulukoita ja kuvia.c) Muodosta ja piirrä edellisiä suoraan Maplella .
d) Kirjoita edellä olevat ideat (pieneksi, 2–3 komentoa) funktioksi taypolkert, joka yksinkertaisesti ottaa argumentikseen (Vaikkapa Maplella saatavan ) derivaattajonon, jossa siis käsiteltävän funktion derivaatat on laskettu kehityskeskuksessa. Funktion tulee palauttaa Taylorin polynomin kerroinjono. (Laskentapiste ei näy Matlab-funktiossa argumenttina, se tulee mukaan jo Maple (tai kynä/paperi)-vaiheessa.) Palauta kertoimet alenevien potenssien mukaan, siis “polyval-sopivasti”. Alku voisi olla tällainen:
function kertoimet=taypolkert(derjono)
% Lasketaan Taylorin polynomin kertoimet. Asteluku määräytyy
% derjonon pituudesta
% derjono: [f(x0),f’(x0),f’’(x0),...]
% pisteet, joissa lasketaan
Testaa funktiotasi ainakin samoilla kuin ennen funktion tekoa. Voi tietysti olla, että haluat mieluummin kirjoittaa funktion muodossa function y=taypol(derjono,x) . Tällöin polyval on mukana ja arvot lasketaan siis vektorissa x. No, tee miten haluat! Vihje: Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1,Taylorin polynomi,Matlabdiffint
- 34. mplDi029.tex (Maple,Matlab)
Laske sopivaa Taylorin polynomia ja siihen liittyvää virhetermiä hyväksi käyttäen likiarvo integraalille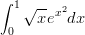
Vertaa laskemaasi approksimaatiota Maplen evalf(Int(..)); - komennon antamaan arvoon.
Pohdittavaksi: Onko Taylorin polynomin käyttö hyvä numeerisen integroinnin menetelmä? Missä tapauksessa on ja missä ei? Vihje: Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1,Taylorin polynomi,Matlabdiffint
- 35. mplDi030.tex (Maple,Matlab)
Muodosta lemniskaatan r2 = cos 2ϕ kaaren pituuden lauseke. Voit integroida välillä [0,π∕4] ja kertoa tuloksen 4:llä.Kokeile integroida Maplella, kenties tulos on hieman yllättävä, laske numeerinen approksimaatio evalf:lla.
Suorita with(student): ja kokeile funktioita trapezoid ja simpson. Huomaa, että integroitava on singulaarinen päätepisteessä, joten näillä täytyy jättää väli hieman vajaaksi. Pääsetkö lähelle oikeaa tulosta näillä välineillä. Katso myös kuvia, niin integrandista kuin integraalifunktiostakin (Niin, Maple osaa tosiaankin sellaisen muodostaa!) Vihje: Avainsanat: mapleDiffint, Mapleperusteet, peruskurssi1,Taylorin polynomi,Matlabdiffint,numeerinen integrointi
- 36. Selitä, miksi näin saadaan exp-funktion katkaistu Taylorin sarja. Suorita sitten Maplella tämäntyylistä:> series(exp(x), x = 0, 10); # tai taylor(…);
> p:=convert(%,polynom);
> c:=coeffs(p,x);
> evalf(%);Selitä, mitä näissä tapahtuu. (Tutki tarvitessasi helpillä komentoja niin Matlabissa kuin Maplessa.)
Piirrä ja taulukoi tulokset.
Vihje:
