
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Harjoitustehtäviä liittyen differentiaaliyhtälöiden ratkaisemiseen ja tutkimiseen Maplessa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mplD0009.tex
Putoavan kappaleen nopeus v = v(t) toteuttaa differentiaaliyhtälön mv′(t) = mg −kv(t)2, jos positiivinen suunta on alaspäin ja ilmanvastus on verrannollinen nopeuden neliöön kertoimella k > 0.
a) Ratkaise differentiaaliyhtälö alkuehdolla v(0) = 0.
b) Mikä on rajanopeus lim t→∞v(t)?
Vihje: Ohjelma ei osaa laskea raja-arvoa, koska se ei tiedä vakioiden etumerkkiä. Lisää käsky assume(m>0 and k>0 and g>0) ja kokeile uudelleen sen jälkeen. - 2. mplD001.tex (infoverkostot (iv) s. 2001) Ratkaise yhtälö
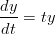
- Muodosta yleinen ratkaisu.
- Määritä vakio ˙C1 alkuehdolle y(0) = 1.
- Ratkaise alkuarvotehtävä suoraan dsolve:lla.
Vihje: Maplen funktio dsolve.
b)-kohdassa voit ottaa ratkaisulausekkeen rhs (Righthand side) kiinni. Tarvitset lisäksi komentoja subs ja solve
c) ?dsolve, [HAM] ss. 162-165Ratkaisu:
> dyht := diff(y(t), t) = t*y(t)
a)
> ylratk := dsolve(dyht, y(t))
b)
> Y := rhs(ylratk)
> solve(subs(t = 0, Y) = 1, ˙C1)
Huom! Dokumenttimoodissa alaviiva pudottaa kursorin alaindeksitasolle.
”copy/paste” tarvitaan ˙C1:lle.
> eval(%)
c)
> dsolve(–dyht, y(0) = 1˝, y(t)) - 3. mplD002.tex (infoverkostot (iv) s. 2001)
Ratkaise differentiaaliyhtälö sijoittamalla ratkaisuehdotus (REh) annettuun yhtälöön tai esim. integroimalla, arvaamalla tms.:
(a) y′ + y = x2 − 2, REh: y = Ce−x + x2 − 2x
(b) y′′ + y = 0, REh: y = a cos x + b sin x
(c) y′′′ = ex,
(d) x + yy′ = 0, REh: x2 + y2 = C (C > 0, vakio).Vihje: (d)-kohta: Derivoi implisiittisesti, ts. oleta, että on olemassa derivoituva funktio x↦y(x) s.e. x2 + y(x) = C ja derivoi puolittain. (Tässä tapauksessa olemassaolo tiedetään, onhan y(x) =
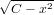 tällainen. Tämän eksplisiittisen lausekkeen käyttö ei silti kannata, se vain
mutkistaa asioita, olkaamme siis implisiittisiä.)
tällainen. Tämän eksplisiittisen lausekkeen käyttö ei silti kannata, se vain
mutkistaa asioita, olkaamme siis implisiittisiä.)
Ratkaisu: mplD002R.mw ja .pdf ON
- 4. mplD0021.tex
Vrt. ... mlD0021 ja mlD0021b
Totea Maple:n avulla suoraan yhtälöön sijoittamalla , että
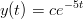
toteuttaa differentiaaliyhtälön y′ = −5y.
Määritä myös diffyhtälön yleinen ratkaisu sekä alkuhdon y(0) = c toteuttava ratkaisu dsolve-komennolla (kts. vihje)
Piirrä ratkaisukäyräparvi, kun vakio c saa 21 arvoa tasavälisesti välillä [0,4]. (Tai suunnilleen tuonverran)
Piirrä paksummalla viivalla alkuehdon y(0) = 1 toteuttava kuvaaja ja merkitse alkupiste rinkulalla.
Huom:Maplen syntaksi muistuttaa läheisesti muPad:ia. Grafiikoiden yhdistämiseen on Maplessa monipuolisemmat välineet.
Vihje: Komentoja: subs,diff,dsolve,plot,with(plots),display
diffyht:=diff(y(t),t) =-5*y(t)
# tai:
diffyht2:=y’(t)=-5*y(t)Näiden käsittely eroaa, edellinen on lauseketyylinen, jälkimmäinen funktiotyylinen, kuten tulostusmuodosta näkyy.
Normaal subs-toimii edellisessä, mutta ei jälkimmäisessä.
Käytä siis alkuosassa edellistä.
?dsolve # Toimii kumpaankin yhtälömuotoon (tottakai).
ratk:=dsolve(–diffyhtalo,y(0)=c˝,y(t))
Y:=subs(ratk,y(t)) # Mieti, logiikka on kohdallaan.
parvi:=seq(Y,c=0..4,0.2) # Sama kuin matlab:n 0:0.2:4
with(plots)
pkuva:=plot([parvi],t=a..b) # a ja b tehtävän mukaan.
?plot,options
display(pkuva,plot([[0,1]],style=point,symbol=circle,symbolsize=20),plot(exp(...),t=...,thickness=3))Grafiikkojen yhdistäminen yleisesti Maplella hoituu display-komennolla (edellyttää with(plots)-komentoa):
display(kuva1,kuva2,kuva3)Vaativuus: 1
Avainsanat: MapleDiffyht, MapleODE, diffyhtälöt, ratkaisukayraparvi
- 5. mplD003.tex [Matlab-versio: ...mlD002.tex] (iv3/2001, harj. 1, teht. 2)
Millä xy-tason käyrillä on ominaisuus: Käyrän tangentin kulmakerroin jokaisessa pisteessä (x,y) on −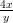 ?
?
Ratkaise yhtälö muuttujien erottelulla (“separation of variables”). Piirrä suuntakenttä isokliineja apuna käyttäen käsin vaikkapa alueessa [−2, 2] × [−2, 2].
Ota sitten Maple avuksi. Kokeile ja selitä!
Vihje: Kts. [HAM] ss. 169-170
> with(DEtools)
> with(plots)Suuntakenttään:DEplot,
grafiikkojen yhdistämiseen: display.
Suoraparven saat tyyliin> yparvi:=seq(...,c=[-2,-1,-.5,.5,2,1]) # tms.
> isokl:=plot([yparvi],x=...)Yleisemmin isokliinit saadaan piirretyksi implicitplot-funktiolla, mutta tässä saatiin ratkaistussa muodossa suoraan.
Avainsanat:MapleDy, diffyhtälöt, suuntakenttä, isokliinit, mplDifferentiaali(yhtälöt)
Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998
- 6. mplD004.tex [Matlab-versio: ...mlD004.tex] (iv3/2001, harj. 1, LV teht. 1-2)
Laskuvarjohyppääjän yhtälö. Oletetaan, että hyppääjän + varustuksen massa = m ja ilmanvastus on verrannollinen nopeuden neliöön, olkoon verrannollisuskerroin = b. Tällöin Newtonin 2. laki antaa liikeyhtälön:
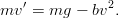
Olkoon yksinkertaisuuden vuoksi m = 1,b = 1 ja g = 9.81m∕s2.
Piirrä suuntakenttä.
Oletetaan, että laskuvarjo aukeaa, kun v = 10m∕s, valitaan tämä alkuhetkeksi t = 0. Piirrä tämä ratkaisukäyrä suuntakenttäpiirrokseen. Yritä nähdä suuntakentästä, että kaikki ratkaisut näyttävät lähestyvän rajanopeutta v ≈ 3.13 ja että ratkaisut ovat joko kasvavia tai pieneneviä (ja millä alkuarvoilla mitäkin, ja mitä tarkoittaa fysikaalisesti)
Määritä rajanopeus suoraan yhtälöstä.
Käytä Matlab-piirroksiin funktiota dfield8 ja Maplessa DEtools-kirjaston DEplot-funktiota.
Vihje: Kts. [HAM] ss. 169-170 tai ?DEplot
> with(DEtools)
> with(plots)Suuntakenttään:DEplot,
grafiikkojen yhdistämiseen: display.
dfield-ohje:
Hae m-tiedosto dfield8 sivulta http://math.rice.edu/˜dfield/ ja sijoita se Matlab-polkusi varrelle.
Kirjoita Matlab-istuntoon : dfield8
Avainsanat: MatlabDy, MapleDy, diffyhtälöt, suuntakenttä, isokliinit, mplDifferentiaali(yhtälöt), mlDifferentiaali(yhtälöt)
Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998
- 7. mplD005.tex (iv3/2001, harj. 1, LV teht. 2)
Muodosta edellä olevan laskuvarjotehtävän (mplD004) analyyttinen ratkaisu muuttujien erottelulla. Määritä edellä mainittu (v(0) = 10)-ratkaisukäyrä. Tarkista ratkaisu Maplella ja kokeile lopuksi Maplen dsolve- komentoa. (Ohje [HAM]-kirjassa.)
Vihje: Ohje analyyttiseen: Muistathan, että osamurtohajoitelma on hyödyllinen rationaalilausekkeen integroinnissa (Maple: convert(lauseke,parfrac,muuttuja); mutta osattava myös käsin).
Avainsanat: MapleDy, diffyhtälöt, muuttujien erottelu, mplDifferentiaali(yhtälöt), mlDifferentiaali(yhtälöt)
Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998
- 8. mplD006.tex (iv3/2001, harj. 1, LV teht. 3)
Vaihdamme tässä LAODE-tyyliseen notaatioon: t on riippumaton muuttuja, x on “riippuva” muuttuja. Kannattaa totutella eri tyyleihin.Ratkaise alkuarvotehtävä x′ =
 − e−t, x(0) = −1. Kyseessä on lineaarinen
epähomogeeninen (EHY). Tämä lasku ei edellytä mitään uutta muuttujien
erottelun lisäksi (ainoastaan uskomista), kaikki on tässä neuvottu.
− e−t, x(0) = −1. Kyseessä on lineaarinen
epähomogeeninen (EHY). Tämä lasku ei edellytä mitään uutta muuttujien
erottelun lisäksi (ainoastaan uskomista), kaikki on tässä neuvottu.
Suorita ratkaisu näin:
- Ratkaise ensin vastaava (HY) x′ =
 (yleinen ratkaisu).
(yleinen ratkaisu).
- Yritä keksiä jokin (EHY):n erityisratkaisu (siis mikä tahansa (EHY):n toteuttava). Keksiminen on helppoa, kun mietit exp-funktion derivointia. (Määräämätön kerroin ratkaistaan sijoittamalla yrite (EHY):yyn).
Lineaaristen teoria sanoo, että (EHY):n yleinen = (HY):n yleinen + (EHY):n erikoinen.
Piirrä myös suuntakenttä ja ratkaisukäyriä (Maple: DEtools[DEplot], Matlab: dfield8 tai suuntak1).
Miten näet suuntakentästä, että yhtälö ei ole autonominen?Avainsanat: MapleDy, lineaariset diffyhtälöt, mplDifferentiaali(yhtälöt)
Viitteet: [LAODE] Golubitzky-Dellnitz: Linear Algebra and Differential Equations using Matlab, Brooks/Cole 1999.
- Ratkaise ensin vastaava (HY) x′ =
- 9. mplD007.tex (iv3/2001, harj. 2, AV teht. 1)
Ratkaise (AA)-tehtävä y′− 2xy = 1, y(0) = −0.5Tässä näyttää siltä, että (EHY):n erikoinen olisi helppo löytää, mutta huomaat pian, että luonnolliset yritteet eivät toimi. (Kyseessähän on lineaarinen, mutta ei-vakiokertoiminen yhtälö.)
Ratkaise vaan sitten kiltisti integroivan tekijän menettelyllä.
Integrointi johtaa erf-funktioon, Maple antaa sen suoraan, voit myös konsultoida KRE-kirjaa hakusanalla erf. Lausu siis ratkaisu erf:n avulla.
Piirrä suuntakenttäpiirros Maplen DEtools-pakkauksen DEplot-funktion avulla (kts [HAM] s. 169), voit toki käyttää myös Matlab:n dfield8-funktiota (ohje alla).
Valitse alkuarvoja y0 väliltä (−1,−0.5) yrittäen löytää kriittistä arvoa y0, joka jakaa ratrkaisukäyrät plus tai miinus ääretöntä lähestyviin. (Tuo kriittinen ratkaisukäyrä on rajoitettu.) Käytä hyväksesi erf-funktion ominaisuutta lim x→∞erf(x) = 1 laskeaksesi tarkan arvon y0:lle.
Vihje: dfield-ohje: Hae m-tiedosto dfield8 sivulta http://math.rice.edu/˜dfield/ ja sijoita se Matlab-polkusi varrelle.
Kirjoita Matlab-istuntoon : dfield8
Avainsanat: MapleDy, diffyhtälöt,erf, mplDifferentiaali(yhtälöt)
Viitteet: [KRE] E. Kreyszig: Advanced Engineering Mathematics, Wiley
[HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998. - 10. mplD008.tex (iv3/2001, harj. 2, AV teht. 2)
Tarkastellaan (AA)-tehtävää xy′ = 4y, y(0) = 1.(a) Osoita, että tehtävällä ei ole ratkaisua. Osoita, että tämä ei ole ristiriidassa ∃1-lauseen kanssa. (Huom: Lauseen avulla ei voi todistaa epäeksistenssiä, koska lauseen ehdot eivä ole välttämättömät.)
(b) Vaihdetaan alkuehdoksi: y(0) = 0. Miten nyt on ratkaisujen laita.
(c) Mitä voit sanoa alkuehdon y(x0) = y0 tapauksessa, jos x0≠0,
(A) suoraan ratkaisukaavan avulla, (B) ∃1-lauseen avulla.Vihje: Tämä on puhtaasti “perinteinen” tehtävä, mutta havainnollistus Maple/Matlab-välineillä on hyvinkin paikallaan.
Avainsanat: diffyhtälöt, ratkaisun (epä)olemassaolo, eksistenssilause, mplDifferentiaali(yhtälöt)
- 11. mplD009.tex (iv3/2001, harj. 2, AV teht. 3)
Muodosta Picardin iteraatiojonon muutama termi (AA)-tehtäville(a) y′ = x + y, y(0) = 0 (b) y′ = x + y, y(0) = −1
(c) y′ = y2, y(0) = 1.Määritä myös tarkka ratkaisu.
Vihje: LV-tehtävässä palataan asiaan Maple-hommana. Tämä on tyypillistä symbolilaskennan vahvuusaluetta.
Avainsanat: diffyhtälöt, ratkaisun (epä)olemassaolo, Picard-Lindelöf-menetelmä, Picardin iteraatio, mplDifferentiaali(yhtälöt)
- 12. Ratkaise yhtälö
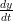 = ty.
Vihje: Maplen funktio dsolve.
= ty.
Vihje: Maplen funktio dsolve.
- 13. mplD010.tex (iv3/2001, harj. 2, LV teht. 1)
Muodosta Picardin iteraatiojonoa pitemmälle kuin AV-tehtävässä samoille (AA)-tehtäville (a), (b), (c) ja lisäksi vielä (d): lle.(a) y′ = x + y, y(0) = 0 (b) y′ = x + y, y(0) = −1
(c) y′ = y2, y(0) = 1. (d) y′ = 3
Laske myös tarkka ratkaisu Maplella ja piirrä se ja iteraatiojonon funktioita. (Jos tuntuu liian pitkältä, niin jätä yksi pois, hyvä olis saada kaikki yhteisesti katetuksi (vaikka parityöskentelyssä sopimalla).
Vihje: Malli: Aputiedostossa mplD010apu.zip on L4Picard.mw,L4Picard.pdf,L4exa2.mw, L4exa2.pdf, kts. myös [HAM] ss. 162–165 (dsolve)ja s. 126 Picard–Lindelöf
Avainsanat: diffyhtälöt, Picard-Lindelöf-menetelmä, Picardin iteraatio, mplDifferentiaali(yhtälöt)
Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998. - 14. mplD011.tex
- Sovella Picardin iteraatiota (tuttuakin tutumpaan) (AA)-tehtävään
y′ = y, y(0) = 1. Osoita, että iteraatiojono lähestyy ratkaisufunktiota y(x) = ex .
- (Olkoon vaihteeksi x(t) .)
Olkoon alkuarvotehtävänä edelleen x′ = x, x(0) = 1.Osoita, että jos lasketaan likiarvo xn = xh(tn) EM:llä pisteessä t = tn käyttäen askelpituutta h, niin xh(tn) = c(h)tn, missä c(h) = (1 + h)1∕h.
Osoita tämän nojalla, että kiinteällä t = tn pätee lim h→0xh(t) = et.
EM = Eulerin menetelmä - Sovella Picardin iteraatiota (tuttuakin tutumpaan) (AA)-tehtävään
- 15. mplD012.tex
Seuraava toistokäsky soveltaa Eulerin menetelmää alkuarvotehtävän y′ = sin(xy), y(0) = 1 ratkaisun likiarvon y(1) laskemiseen. Kokeile käskyjä askelpituuksilla h = 0.25,h = 0.1,h = 0.01 ja h = 10−4. Mikä menee pieleen viimeisessä kohdassa?f:=(x,y)-> sin(x*y);
Digits:= 4;
n:= 4;
h:=1/n;
y[0] := 1;
for k from 0 to n-1 do # (paina tässä kohti Shift+Enter)
y[k+1]:= evalf(y[k]+h*f(k*h,y[k])) # (samoin)
end do;Piirrä Eulerin murtoviivat eri väreillä samaan koordinaatistoon. Vihje: Datan piirto sujuu nykyisin “Matlab-tyylisesti”:
> xlista:=[seq(j*h,j=0..n)];
> ylista:=[seq(y[j],j=0..n)]
> plot(xlista,ylista)[HAM]-viitteessä ss. 94-96 esitetyt tavat pisteparien listana toimivat myös, mutta s. 96 zip-temppu ei ole enää tarpeen. Viitteet: [HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998.
- 16. mplD013.tex
Ratkaise alkuarvotehtävä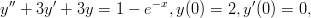
ja piirrä ratkaisun kuvaaja välillä 0 ≤ x ≤ 10. Vihje: Diffyhtälön saat ratkaistua komennolla dsolve. Yhtälössä esiintyvät derivaatat voit ilmoittaa komennolla diff, ja derivaatan pisteessa 0 voit ilmaista derivaattaoperaattorilla D(y)(0).
- 17. mplD014.tex Maple,Matlab
- Ratkaise alkuarvotehtävä
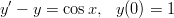
analyyttisesti Maplella ja numeerisesti Matlabilla. Piirrä ratkaisukäyrä.
- Anna alkuarvoksi symboli c ja piirrä ratkaisukäyräparvi sopivalla välillä,
kun c = −0.9,−0.8,…, 0.
Miltä parvi näyttää suurilla x :n arvoilla. Tässä pitäisi erottua kolmenlaista käytöstä.
Vihje: Maple: dsolve, Matlab: ode45
Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu.
Viitteet:
Coombes et al: Differential equations with Maple, Wiley
Boyce - DiPrima’s: Elementary Differential Equations and Boundary Value Problems,Wiley - Ratkaise alkuarvotehtävä
- 18. mplD015.tex Maple,Matlab
Tarkastellaan (AA)-tehtävää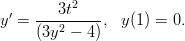
(a) Laske EM:llä ratkaisuapproksimaatiot pisteissä t = 1.2, 1.4, 1.6, 1.8 käyttäen askelta h = 0.1 .
(b) Tee sama askeleella h = 0.05 .
(c) Vertaa tuloksia.
(d) Piirrä suuntakenttä ja ratkaisuapproksimaatioita, sekä EM-ratkaisuja. Osaatko selittää, miksi EM toimii kohtuullisesti alussa, mutta kelvottomasti lopussa?
Vihje: Eulerin menetelmää voi tässä käyttää ohjelman (MMM) laskintyylillä, kuten edellä tai sitten oikeaksi funktioksi koodatulla versiolla, annetaan tässä nuo koodit.
Eulerin menetelmän koodit (sisältyvät myös apupakettiin *apu.zip):
Maple: [HAM s. 206] (copy/paste → Maple-istuntoon)Euler:=proc(f,a,b,ya,m)
local n,h,t,y;
h:=evalf((b-a)/m);
t[0]:=a;y[0]:=ya;
for n from 0 to m do
y[n+1]:=y[n]+h*f(t[n],y[n]);
t[n+1]:=t[n]+h;
end do;
seq([t[n],y[n]],n=0..m);
end:Esim: y′ = t − y2
f:=(t,y)->t-y^2;
e3:=Euler(f,0,5,1,3);
plot([e3]);Matlab: (Kts. vastaava Matlab-teht.)
Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu.
Viitteet:
[KRE] E. Kreyszig: Advanced Engineering Mathematics, Wiley
[HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998. - 19. mplD016.tex (vrt. Matlab: mlD007.tex)
Tarkastellaan (AA)-tehtävää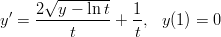
- Eulerin menetelmällä askelpituudella h = 0.1,
- Heunin menetelmällä askelpituudella h = 0.2,
- RK4- menetelmällä askelpituudella h = 0.4.
Määritä tarkka ratkaisu Maple:n dsolve-komennolla ja laske sen avulla virheet, piirrä ja taulukoi kussakin tapauksessa.
Huomaa, että näillä askelpituuksien valinnoilla funktion arvojen laskentamäärät ovat samat.
Vihje: Eulerin menetelmän koodit (sisältyvät myös apupakettiin mplD016apu.zip):
Maple: [HAM s. 206] (copy/paste → Maple-istuntoon)Euler:=proc(f,a,b,ya,m)
local n,h,t,y;
h:=evalf((b-a)/m);
t[0]:=a;y[0]:=ya;
for n from 0 to m do
y[n+1]:=y[n]+h*f(t[n],y[n]);
t[n+1]:=t[n]+h;
end do;
seq([t[n],y[n]],n=0..m);
end:Esim: y′ = t − y2
f:=(t,y)->t-y^2;
e3:=Euler(f,0,5,1,3);
plot([e3]);Laitetaan myös Heun ja RK4
Matlab: (Kts. vastaava Matlab-teht.)
Huom: Tästä voi kehitellä monenlaisia tehtävävariaatioita, myös ilman numeeristen menetelmien korostusta.
Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu.
Viitteet:
[KRE] E. Kreyszig: Advanced Engineering Mathematics, Wiley
[HAM] Heikki Apiola: Symbolista ja numeerista matematiikkaa Maple-ohjelmalla, Otatieto 588, 1998. - 20. mplD017.tex, mlD007.tex
Huomasimme, että eksponentiaalinen kasvumalli, ns. Malthus’n laki y′ = ky ei toimi USA:n väestödataan pitkällä aikavälillä. Mallia voidaan tarkentaa lisäämällä sopiva kasvua rajoittava termi, tällöin johdutaan ns. logistiseen kasvulakiin:y′ = ay − by2
USA:n väestödataan liityen Verhulst arvioi v. 1845 arvot a = 0.03 ja b = 1.610−4, kun t mitataan vuosissa ja väkiluku y(t) miljoonissa.
Opettajalle: Tehtävä voidaan käsitellä ehkä luontavamminkin kokonaan erillisenä numeeristen diffyhtälöratkaisujen opetuksesta. Tällöin otetaan vain alla olevat kohdat (c) ja/tai (d).
(a) Ratkaise tehtävä (y(0) = 5.3) Eulerin menetelmällä käyttämllä askelpituussa h = 10
(b) rk4:llä käyttäen n. nelinkertaista askelta (voit kokeilla pienempiäkin)
(c) Matlabin ode45:llä.
(d) Laske analyyttinen ratkaisu Maplella (kyseessähän on Bernoullin yhtälö.
Piirrä kuvia ja laske kaikissa tapauksessa ratkaisujen arvot annetuissa taulukkopisteissä. (ode45-tapauksessa onnistuu ainakin sovittamalla dataan splini funktiolla spline, joka on maailman helppokäyttöisin.)
kts. http://www.math.hut.fi/teaching/v/matlab/opas.html#splinit
(Nykyään (2012) ei tarvita erillistä splinisovitusta, laskentapisteet voidaan antaa suoraan ode45-funktiolle syötteenä.) Vihje:function [T,Y]=eulerS(f,Tspan,ya,n)
% Tämä vain kehittely- ja opettelutarkoituksessa.
% Funktio eulerV hoitaa niin skalaari- kuin vektoriversion.
% (24.2.04, modifioitu 21.8.2010)
% Esim: y’=t+y, y(0)=1
% f=@(t,y)t+y
% [T,Y]=eulerS(f,[0 4],1,6), plot(T,Y,T,Y,’.r’);shg
a=Tspan(1);b=Tspan(2);
h=(b-a)/n;
Y=zeros(n+1,1);T=(a:h:b)’; %Pystyvektorit yhdenmukaisesti ode45:n
Y(1)=ya; % kanssa
for j=1:n
Y(j+1)=Y(j)+h*f(T(j),Y(j));
end;Viitteitä:
http://math.aalto.fi/opetus/kp3-ii/06/L/L14dynumkalvot.pdf
http://www.math.hut.fi/˜apiola/matlab/opas/lyhyt/esim/eulerS.m
(Listaus yllä) - 21. mplD018.tex, mlD008.tex
Tarkastellaan yhtälöä y′ = −2α(t − 1)y. Ratkaise aluksi analyyttisesti (saat käyttää Mapleakin.)Totea kuvasta ja derivaattaehdosta yhtälön stabiilisuus/epästabiilisuusalueet. Ota kuvassa ja aina tarvittaessa vaikkapa α = 5.
Ratkaise yhtälö sekä Eulerilla että BE:llä. Sopivia arvoja voisivat olla vaikkapa h = 0.2, väli: [1, 4.5], y(1) = 1.
Vertaa kokeellisesti stabiilisuukäyttäytymistä teorian ennustamaan ja pane merkille, miten epästabiilisuus käytännössä ilmenee.
Tämä tehtävä soveltuu erityisen hyvin Maplella tehtäväksi, se on pitkälle ideoitu [HAM] sivulla 124, myös Euler ja BE ovat valmiina. (Koodit saa kurssin maple-hakemistosta.) ** Tulee aputiedostoon **** apu puuttuu, editoi viitteet! ** Vihje:
Viitteitä:
http://math.aalto.fi/opetus/kp3-ii/06/L/L14dynumkalvot.pdf
http://www.math.hut.fi/˜apiola/matlab/opas/lyhyt/esim/eulerS.m
(Listaus yllä) - 22. mplD019.tex [mplP017.tex]
Opiskelija ottaa lainaa 10000 euroa hetkellä k = 0 ja ryhtyy maksamaan sitä takaisin kuukauden päästä hetkellä k = 1. Kuukausikorko on 1% (huh!) ja takaisinmaksu tapahtuu kiintein maksuerin 450 EUR/kkOlkoon yk k:n kuukauden kuluttua jäljellä olevan velan määrä. Kirjoita differenssiyhtälö yk:lle.
Muodosta taulukko ja graafinen esitys, jossa on pisteet (k,yk), ja selvitä sen perusteella, miten kauan velan maksu kestää ja miten paljon rahaa opiskelijaparka käyttää koko projektiin.
Luokittelu: Differenssi- ja differentiaaliyhtalot, Maple-perusteet.
Vihje:
- 23. Seuraava toistokäsky soveltaa Eulerin menetelmää alkuarvotehtävän y′ = sin(xy), y(0) = 1 ratkaisun likiarvon y(1) laskemiseen. Kokeile käskyjä askelpituuksilla h = 0.25,h = 0.1,h = 0.01 ja h = 10−4. Mikä menee pieleen viimeisessä kohdassa?f:=(x,y)-> sin(x*y);
Digits:= 4;
n:= 4;
h:=1/n;
y[0] = 1;
for k from 0 to n-1 do (paina tässä kohti Shift+Enter)
y[k+1]:= y[k]+h*f(k*h,y[k]) (samoin)
od;Vihje:
- 24. Ratkaise alkuarvotehtävä
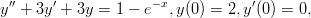
ja piirrä ratkaisun kuvaaja välillä 0 ≤ x ≤ 10. Vihje: Diffyhtälön saat ratkaistua komennolla dsolve. Yhtälössä esiintyvät derivaatat voit ilmoittaa komennolla diff, ja derivaatan pisteessa 0 voit ilmaista derivaattaoperaattorilla D(y)(0).
- 25. Ratkaise differentiaaliyhtälöryhmä
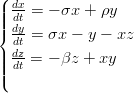
numeerisesti välillä [0, 20], kun σ = 10,ρ = 28 ja β = 8∕3. Piirrä ratkaisukäyrät samaan kuvaan, ja piirrä käyrät x(t) ja z(t) parametrisesti. Tämän jälkeen piirrä 3-ulotteinen parametrisoitu käyrä kaikista koordinaateista.
Onko ratkaisu rajoitettu? Suppeneeko se kohti jotain arvoa?
Kokeile muuttaa alkuarvoja, sekä parametrien arvoja. Vallitsevan teorian mukaan systeemi on kaoottinen dynaaminen systeemi, jonka käyttäytyminen voi muuttua merkitsevästi jo pienistä muutoksista lähtötilanteessa; itse asiassa termi perhosvaikutus keksittiin kuvaamaan juuri tämän systeemin käytöstä. Vihje: Kolmiulotteinen parametrisoitu käyrä (tai pistejoukko) piirretään MATLABissa funktiolla plot3.
- 26. Maple,Matlab (H2T10)
- Ratkaise alkuarvotehtävä
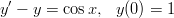
analyyttisesti Maplella ja numeerisesti Matlabilla. Piirrä ratkaisukäyrä.
- Anna alkuarvoksi symboli c ja piirrä ratkaisukäyräparvi sopivalla välillä,
kun c = −0.9,−0.8,…, 0.
Miltä parvi näyttää suurilla x :n arvoilla. Tässä pitäisi erottua kolmenlaista käytöstä.
Vihje: Maple: dsolve, Matlab: ode45
Avainsanat: Differentiaaliyhtälö, alkuarvotehtävä, analyyttinen ratkaisu, numeerinen ratkaisu.
- Ratkaise alkuarvotehtävä
- 27. Kirjoita heiluriyhtälö Θ′′ +
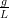 sin(Θ) = 0 ensimmäisen kertaluvun systeemiksi, tai
toisen kertaluvun differentiaaliyhtälöksi. Voit ottaa g∕L = 1.
sin(Θ) = 0 ensimmäisen kertaluvun systeemiksi, tai
toisen kertaluvun differentiaaliyhtälöksi. Voit ottaa g∕L = 1.
Laske ratkaisu sopivalla aikavälillä (esim.
![[0,10]](mapleHarDY17x.png) ) ja kolmella erilaisella alkuarvolla,
joilla saat erityyppiset ratkaisut.
) ja kolmella erilaisella alkuarvolla,
joilla saat erityyppiset ratkaisut.
Piirrä ratkaisukäyrät aikatasoon ja trajektorit faasitasoon.
- 28. Ratkaise RA-tehtävä
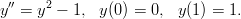
Siirry sitten tyyppiin numeric, homma sujuu ongelmitta.
Muutaman kokeilun jälkeen huomasin, ettei sujukaan. Numeerisen ratkaisun määritteleminen parametrista riippuvaksi funkioksi on aikamoista temppuilua, tällaisella kurssilla ei kannata siihen paneutua, koska Matlab-ratkaisu on hyvin selkeä ja ongelmaton.
Muutetaan tehtävä helpommaksi:
Suorita Maplella suoraan reuna-arvotehtävän ratkaisu (luultavasti Maple laskee sen differessimenetelmällä). Syntaksi on aivan sama kuin alkuarvotehtävälle, nyt vain annetaan pelkät reunaehdot.
Helpin esimerkkien avulla pääset kiinni ratkaisufunktioon.
- 29.
- Osoita, että funktio arctan
 toteuttaa Laplacen
osittaisdifferentiaaliyhtälön
toteuttaa Laplacen
osittaisdifferentiaaliyhtälön
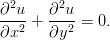
(Tällaisia funktioita sanotaan harmonisiksi funktioiksi.)
- Oletetaan, että funktioilla u(x,y) ja v(x,y) on jatkuvat toiset
osittaisderivaatat ja ne toteuttavat ns. Cauchy-Riemannin yhtälöt:
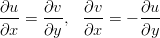
Osoita, että u ja v ovat harmonisia.
- Olkoon f(x,y) = x3y2 +x4 sin y +cos(xy). Laske osittaisderivaatat f xxy, fxyx, fyxx ja totea, että ne ovat samat.
- Osoita, että funktio arctan
