
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Maple harjoitustehtäviä liittyen lineaarialgebraan ja matriisien kanssa toimimiseen Maplessa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. H2T12.tex/mlCF07.tex/mplCF07.tex // Matlab,Maple,[Mathematica]
W.A Mozartin(1756-1791) sävellyksiä indeksoidaan Köchel-luvuilla, jotka ilmaisevat teosten sävellysjärjestyksen. Alla on eräitä Köchel-lukuja, ja vastaavien teosten sävellysvuosia.
Number Year
1 1761
75 1771
155 1772
219 1775
271 1777
351 1780
425 1782
503 1786
575 1789
626 1791Käyttäen tätä dataa, arvioi teoksen Sinfonia Concertanten sävellysvuosi, kun tiedetään, että sen Köchel-numero on 364. Vihje: Piirrä ensin datapisteet tasoon, ja päätä millaista menetelmää kannattaa käyttää. Epäilemättä sopivan asteista PNS-polynomia. Suorita joitakin sovituksia, ja tarkista sitten tulos vaikka Wikipediasta.
- 2. Maple tai Matlab
Tutkitaan nk. Rungen ilmiötä. Laske funktion g(x) = 1∕(1 + x2) arvoja tasaisin välein väliltä [−5, 5], ja tee näihin pisteisiin perustuva polynominen interpolaatio. Piirrä sekä g(x) että P(x) samaan kuvaan. Mitä huomaat, kun valittujen datapisteiden määrää tihennetään?Kokeile interpolointia silloin, kun datapisteitä ei valita tasavälisesti, vaan ne valitaan Chebyshev-pisteiden
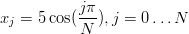
mukaan. Vihje: Polynominen interpolaatio kannattaa tehdä MATLAB-funktiolla polyfit. Funktio g kannattaa määritellä funktiokahvan avulla: g = @(x)1./(1+x.^2). Tasavälisiä pisteistä saa funktiolla linspace
Sopii aivan yhtä hyvin Maplelle.
- 3. mplCF01.tex [Matlab: ../../matlabteht/mlCurveFit/mplCF01.tex]
Opettajalle: Tehtävän alkuperäinen tarkoitus on demonstroida luontevaa, nautitta vaa Maple-työskentelyä. [Sopii myös oikein hyvin Matlab- tehtäväksi. Matlabissa on valmiina polyder-funktio, jonka ohjelmointi on sinänsä myös oikein sopiva pikku harjoitustehtävä. Tässä tehtävässä ei ole tarvetta/syytä käyttää symbolic toolboxia.]
Hermiten interpolaatio: Interpolaatioehdoissa esiintyy myös derivaattoja.
Määritä 4. asteen polynomi p, joka toteuttaa ehdot:
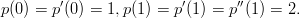
(a) Käsittele polynomi lausekkeena.
Tarkista tulos sopivasti subs-komennoilla ja piirrä kuva/kuvia polynomista ja derivaatoista.(b) Käsittele polynomi funktiona.
Huom: 5 ehtoa ja 5 tuntematonta kerrointa ⇒ järkevän tuntuinen tehtävä. Yleisesti “järkevälläkään” Hermiten interpolaatiotehtävällä ei aina ole yksikäsitteistä ratkaisua (kuten ei neliömatriisin määräämällä lineaarisella yhtälöryhmälläkään – siitähän on kyse). Pelkkiä funktion arvoja koskevalla interpolaatiotehtävällä aina on (koska “Vandermonden neliömatriisi” on aina ei-singulaarinen).
Tässä opetellaan erityisesti Maplen kätevää ratkaisutekniikkaa. Vihje: Kirjoita polynomi lausekkeeksi tyyliin:p:=a*x^4+b*x^3 + .... ,
missä a,b,…,e ovat määrättävät kertoimet.Derivaatta: diff
Arvojen (x=0,x=1) sijoittaminen p:n lausekkeeseen: subs
Yhtälön ratkaiseminen: solveKaikista saat tietoa näin ?diff, ...
- 4. mplCF03.tex, [Matlab: ../../matlabteht/mlCurveFit/mlCF15.tex]
Opettajalle: (a)-kohta sopii ensitutustumiseen.
(b)-kohta on sikäli huono, että virhetermin suuruusluokka on toisesta maailmasta (opettavaista kylläkin, mutta alkajaisiksi vaatii ainakin varoituksen).
Lisää tehtävän opetuksia ratkaisutiedostoissa.(a) Muodosta interpolaatiopolynomi pisteistölle, joka saadaan laskemalla funktion cos(1 + x2) arvot tasavälisessä x-pisteistössä, jossa on 7 pistettä välillä [0, 3].Piirrä samaan kuvaan funktio, datapisteet ja interpolaatiopolynomi.
(b) Arvioi (Lagrangen) interpolaatiokaavan virhetermin avulla interpolaatiovirheen yläraja yo. välillä ja vertaa todelliseen.
Lause Olkoot x0,x1,…,xn erilliset pisteet ja f (n + 1) kertaa jatkuvasti derivoituva funktio xk−pisteet sisältävällä välillä. Jos pn on (1-käs) dataan (xk,f(xk)) liittyvä interpolaatiopolynomi, niin
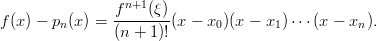
Vihje: Tässä on mahdollista harrastaa Maplen ja Matlabin yhteistyötä. Virhekaavan derivaatta muodostetaan tietysti Maplella ja lauseke sievennetään. Itse asiassa piirtämällä ja poimimalla kuvasta maksimipisteen koordinaatit, saadaan riittävän hyvä arvio.
Toinen mahdollisuus on käyttää Matlabin symbolic toolboxia.Tulotermin voisi hoitaa tehokkaimmin Matlabissa ottamalla tiheän diskretoinnin ja käyttämällä max-funktiota. Maplessakin on max-funktio, lakenta on Matlabissa tehokkaampaa.
Miten tulotermi lasketaan Matlabissa? Vaikka tähän tapaan:
1. x=linspace(....,N)
2. Tedään matriisi X, jossa x-vektoreita allekkain n+1 kpl.
3. Tehdään matriisi X0, jossa rivitx0 x0 ... x0 N kpl.
x1 x1 ... x1 N kpl.
...
xn xn ... xn N kpl.
Nämä syntyvät vaikka meshgrid-komennolla tai ulkotuloilemalla ykköspystyvektorilla.
4. Vähennetään matriisit ja prod()). Sitten vain abs ja max kehiin.Tosi Matlabmaista! (Ei moitita, vaikka tekisit for-loopin, vain 8 kertaa käydään, mutta hyvä ymmärtää Matlabin hienoa matriisiajattelua, muistiahan ei nykyisin tarvitse säästellä.)
Avainsanat: Interpolaatio, käyrän sovitus, interpolaatiovirhe, Lagrange
- 5. mlCF07.tex/mplCF07.tex // Matlab,Maple,[Mathematica]
W.A Mozartin(1756-1791) sävellyksiä indeksoidaan Köchel-luvuilla, jotka ilmaisevat teosten sävellysjärjestyksen. Alla on eräitä Köchel-lukuja, ja vastaavien teosten sävellysvuosia.
Number Year
1 1761
75 1771
155 1772
219 1775
271 1777
351 1780
425 1782
503 1786
575 1789
626 1791Käyttäen tätä dataa, arvioi teoksen Sinfonia Concertanten sävellysvuosi, kun tiedetään, että sen Köchel-numero on 364. Vihje: Piirrä ensin datapisteet tasoon, ja päätä millaista menetelmää kannattaa käyttää. Epäilemättä sopivan asteista PNS-polynomia. Suorita joitakin sovituksia, ja tarkista sitten tulos vaikka Wikipediasta.
- 6. Maple tai Matlab
Tutkitaan nk. Rungen ilmiötä. Laske funktion g(x) = 1∕(1 + x2) arvoja tasaisin välein väliltä [−5, 5], ja tee näihin pisteisiin perustuva polynominen interpolaatio. Piirrä sekä g(x) että P(x) samaan kuvaan. Mitä huomaat, kun valittujen datapisteiden määrää tihennetään?Kokeile interpolointia silloin, kun datapisteitä ei valita tasavälisesti, vaan ne valitaan Chebyshev-pisteiden
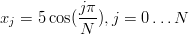
mukaan. Vihje: Polynominen interpolaatio kannattaa tehdä MATLAB-funktiolla polyfit. Funktio g kannattaa määritellä funktiokahvan avulla: g = @(x)1./(1+x.^2). Tasavälisiä pisteistä saa funktiolla linspace
Sopii aivan yhtä hyvin Maplelle.
- 7. H2T14.tex/mlCF13.tex/mplCF13.tex
Matlab,Maple,[Mathematica]Yhdysvaltojen perustuslaki vaatii, että maassa suoritetaan joka kymmenes vuosi väestönlaskenta. Ohessa on väestönlaskennan tuloksia sadoissa miljoonissa asukkaissa viime vuosisadalta.
1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 76 92 106 122 132 150 179 203 226 248
Tee polynomi-interpolointi datalle, ja ennusta väestön määrä vuonna 2010. Kuinka ennusteesi suhtautuu laskennan todelliseen tulokseen: 308,745,538 laskettua asukasta?Sovita myös eriasteisia PNS-polynomeja, vrt. Matlab Censusgui, lue Molerista: http://www.mathworks.se/moler/interp.pdfNum. Comp. with Matlab, interpolation Vihje:
