Polynomit
Contents
Lyhyen oppaan polynomi-osa:
http://math.aalto.fi/~apiola/matlab/opas/lyhyt/polynomit.html
Polynomin esitys
Polynomi esitetään Matlab:ssa kertoimien vektorina korkeimman asteisesta alkaen. Jos jokin potenssi polynomista puuttuu, on vastaava kerroin luonollisesti = 0. Esim:
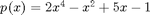
Polynomin maaraa kerroinvektori [2,0,-1,5,-1] .
c = [2 0 -1 5 -1]
c =
2 0 -1 5 -1
Polynomin arvo: polyval
polyval(c,1) % Polynomin arvo pisteessä x=1
ans =
5
polyval toimii myös vektorille x (tietysti, koska kyseessä on Matlab) Niinpä voidaan heti piirtää:
x=linspace(-2,2);
plot(x,polyval(c,x))
grid on
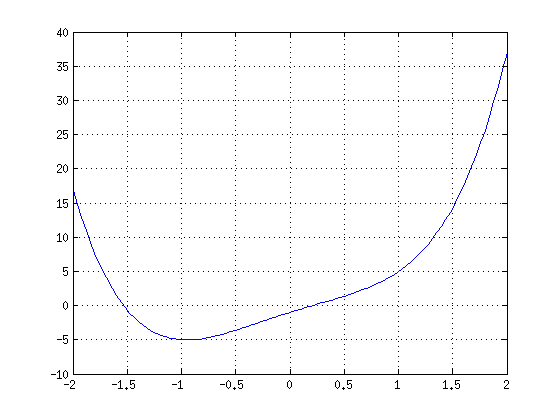
Polynomin nollakohdat, roots
r=roots(c)
% Kuten kuvastakin vaikuttuu, 2 reaalijuurta ja 2 kompleksi.
r = -1.5315 + 0.0000i 0.6618 + 1.0641i 0.6618 - 1.0641i 0.2079 + 0.0000i
Esim: Ykkösen n:nnet juuret:
Ratkaistaan polynomiyhtälö 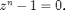
Katsotaan ensin 3. asteen (kuutiojuuren) tapaus
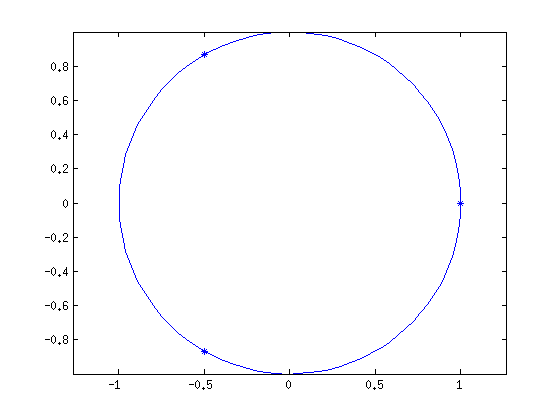
n=3 c=[1 0 0 -1] % z^3 -1 juuret=roots(c) plot(juuret,'*'); hold on t=linspace(0,2*pi); plot(exp(i*t)) axis equal
n =
3
c =
1 0 0 -1
juuret =
-0.5000 + 0.8660i
-0.5000 - 0.8660i
1.0000 + 0.0000i
Yleinen tapaus (esim: n=10)
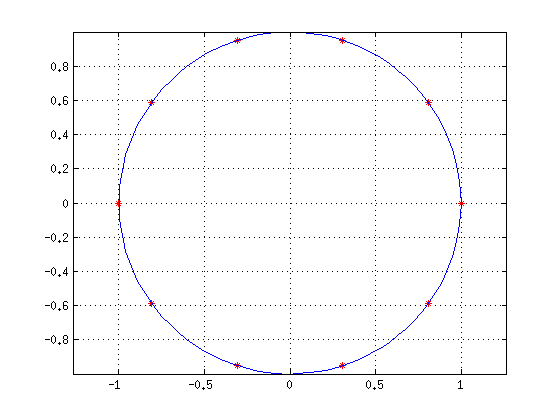
hold off n=10 % Muuttele c=[1 zeros(1,n-1) -1] juuret=roots(c) plot(juuret,'*r'); hold on t=linspace(0,2*pi); plot(exp(i*t)) axis equal;grid on shg
n =
10
c =
1 0 0 0 0 0 0 0 0 0 -1
juuret =
-1.0000 + 0.0000i
-0.8090 + 0.5878i
-0.8090 - 0.5878i
-0.3090 + 0.9511i
-0.3090 - 0.9511i
0.3090 + 0.9511i
0.3090 - 0.9511i
1.0000 + 0.0000i
0.8090 + 0.5878i
0.8090 - 0.5878i
c=[1 zeros(1,n) -1] juuret=roots(c)
c =
1 0 0 0 0 0 0 0 0 0 0 -1
juuret =
-0.9595 + 0.2817i
-0.9595 - 0.2817i
-0.6549 + 0.7557i
-0.6549 - 0.7557i
-0.1423 + 0.9898i
-0.1423 - 0.9898i
0.4154 + 0.9096i
0.4154 - 0.9096i
1.0000 + 0.0000i
0.8413 + 0.5406i
0.8413 - 0.5406i
Tarkistus
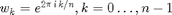
plot(exp((0:n)*2*pi*i/n),'b--')
