3d-grafiikkaa
Contents
http://math.aalto.fi/~apiola/matlab/opas/lyhyt/grafiikka.html#sec:3d
clear close all x=-2:.1:2; y=x; % x-ja y-akselin diskretoinnit tässä samoja. [X,Y]=meshgrid(x,y); % X ja Y määräävät xy-alueen hilapisteistön. size(X), size(Y)
ans =
41 41
ans =
41 41
Z=exp(-X.^2-Y.^2); % Korkeusmatriisin arvot hilapisteissä. % Huomaa "pisteittäiset" laskutoimitukset. surf(x,y,Z) % surf-funktio "asettaa maton % sauvametsän päälle".
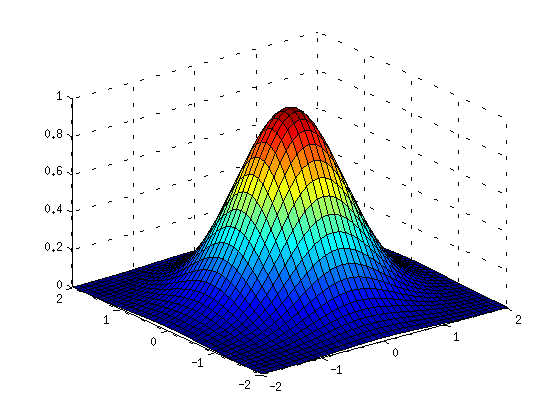
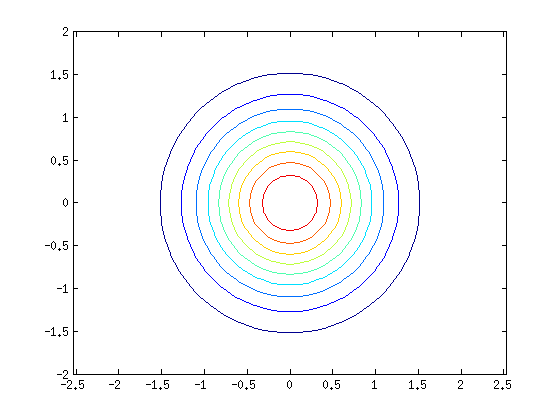
figure contour(x,y,Z) % Korkeuskäyräpiirros axis equal
ezcontour(@(x,y)exp(-x.^2 - y.^2),[-2 2 -2 2]) % "easycontour" Tassa ei tarvita meshgridiä. axis equal
Mita meshgridissa tapahtuu? Katsotaan pienillä datoilla.
close all
x=0:3
y=-2:0
[X,Y]=meshgrid(x,y)
x =
0 1 2 3
y =
-2 -1 0
X =
0 1 2 3
0 1 2 3
0 1 2 3
Y =
-2 -2 -2 -2
-1 -1 -1 -1
0 0 0 0
X:ssa x-sarakkeita y:n pituuden verran vierekkain Y:ssa y-riveja x:n pittuden verran allekkain
Jonoutetaan kumpikin pitkiksi sarakkeiksi:
Hilan vastinkoordinaatit asettuvat paikalleen.
[X(:) Y(:)] plot(X(:),Y(:),'*') axis off shg
ans =
0 -2
0 -1
0 0
1 -2
1 -1
1 0
2 -2
2 -1
2 0
3 -2
3 -1
3 0

Muista: plot(X,Y) piirtää samankokoisten matriisien vastinsarakkeet.
plot(X,Y) hold on plot(X',Y') shg % Niinpä koordinaattiristikko syntyy tälläkin tavalla näppärästi.
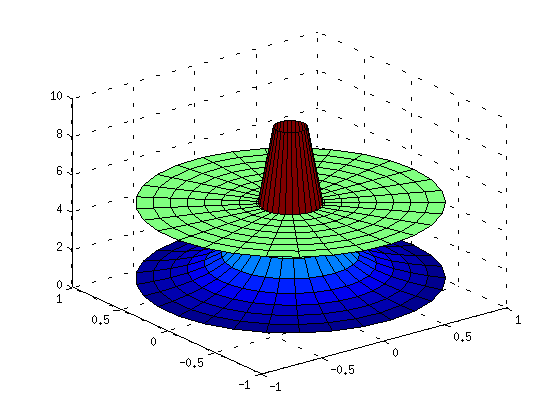
Napakoordinaatistoon, pinta ympyräalueen päällä
clf t=linspace(0,2*pi,30); r=linspace(0,1,10); X=r'*cos(t);Y=r'*sin(t); % Ulkotulot: (pysty_v)*(vaaka_v) mesh(X,Y,zeros(size(X))) % Nollataso shg
figure
Z=1./(sqrt(X.^2+Y.^2));
surf(X,Y,Z)
hold on
surf(X,Y,5*ones(size(Z)))
shg