Eulerin menetelmä

y_n+1=y_n+h f(t_n,y_n)

Maple-esimerkki-istunto

> dy:=diff(y(t),t)=t*sqrt(y(t));

                                   d               1/2
                           dy := ---- y(t) = t y(t)
                                  dt
> y:='y':dy:='dy':
> DY:=dy;

                                   d               1/2
                           DY := ---- y(t) = t y(t)
                                  dt
# Tämä siksi, että DEplot näkyy tallettavan dy-muuttujaan jonkin DE-tietorakenteen
--------------------------------------------------------------------------------
> with(DEtools):
--------------------------------------------------------------------------------
> sk:=DEplot(dy,[t,y],t=0..2,y=2..5,arrows=THIN):  # Maple V.3
--------------------------------------------------------------------------------
> 
--------------------------------------------------------------------------------
> f:=(t,y)->t*sqrt(y);

                             f := (t,y) -> t sqrt(y)
--------------------------------------------------------------------------------
> t[1]:=t[0]+h;y[1]:=y[0]+h*f(t[0],y[0]);

                                t[1] := t[0] + h

                                                    1/2
                          y[1] := y[0] + h t[0] y[0]
--------------------------------------------------------------------------------
> h:=0.1;t[0]:=1;y[0]:=2;

                                     h := .1

                                    t[0] := 1

                                    y[0] := 2
--------------------------------------------------------------------------------
> for i from 1 to 4 do t[i+1]:=t[i]+h;y[i+1]:=evalf(y[i]+h*f(t[i],y[i])) od;

                                   t[2] := 1.2

                               y[2] := 2.302390913

                                   t[3] := 1.3

                               y[3] := 2.484474490

                                   t[4] := 1.4

                               y[4] := 2.689383296

                                   t[5] := 1.5

                               y[5] := 2.918974046
> for i from 1 to 10 do t[i+1]:=t[i]+h;y[i+1]:=evalf(y[i]+h*f(t[i],y[i])) od:
--------------------------------------------------------------------------------
> eupts:=seq([t[i],y[i]],i=0..11);

                                 1/2
  eupts := [1, 2], [1.1, 2 + .1 2   ], [1.2, 2.302390913], [1.3, 2.484474490],

      [1.4, 2.689383296], [1.5, 2.918974046], [1.6, 3.175249125],

      [1.7, 3.460356785], [1.8, 3.776591367], [1.9, 4.126393540],

      [2.0, 4.512350541], [2.1, 4.937196421]
--------------------------------------------------------------------------------
> eu:=plot([eupts],t=0..2,y=2..5):
--------------------------------------------------------------------------------
> with(plots):
--------------------------------------------------------------------------------
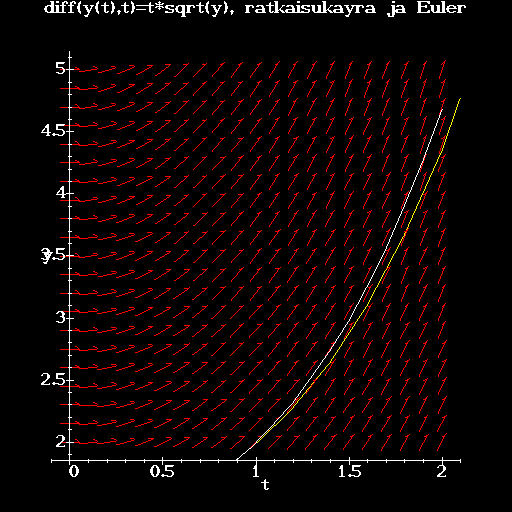
> display({sk,eu});
--------------------------------------------------------------------------------
> tarkka:=dsolve({DY,y(1)=2},y(t));

                                            2          1/2 2
                     tarkka := y(t) = (1/4 t  - 1/4 + 2   )
--------------------------------------------------------------------------------
> z:=rhs(tarkka);

                                      2          1/2 2
                           z := (1/4 t  - 1/4 + 2   )
--------------------------------------------------------------------------------
> tarplot:=plot(z,t=1..2,color=magneta,title=`diff(y(t),t)=sqrt(y), ratkaisukayra ja Euler`):
--------------------------------------------------------------------------------
> display({sk,eu,tarplot});
--------------------------------------------------------------------------------
>