| takaisin |
| Välikoe 2 18.12.2007 | |||||
| 1 | 2 | 3 | 4 | summa | |
| 51170D | 2 | 6 | 0 | 6 | 14 |
| 55603L | 4 | 6 | 3 | 3 | 16 |
| 64611N | 4 | 6 | 0 | 6 | 16 |
| 66650V | 4 | 5 | 0 | 6 | 15 |
| 66931R | 3 | 0 | 0 | 4 | 7 |
| 67195N | 4 | 2 | 0 | 6 | 12 |
| 67221W | 4 | 0 | 0 | 6 | 10 |
| 67330R | 0 | 3 | 0 | 6 | 9 |
| 67566C | 4 | 0 | 0 | 6 | 10 |
| 69050E | 4 | 2 | 0 | 6 | 12 |
| 69292W | 4 | 6 | 3 | 3 | 16 |
| 69880V | 4 | 6 | 0 | 6 | 16 |
| 69998C | 4 | 0 | 0 | 6 | 10 |
| keskiarvo | 12,54 | ||||
Keskiarvo oli matala verrattuna edelliseen tenttiin, joten ilmeisesti koko kurssin pisterajat laskevat hieman. Kurssiarvosanat annetaan viikonlopun aikana.
1a) Kenttä on F(x,y)=(1,0). Mikon piirrustuksen mukaan se näyttää tällaiselta:

Jos jäävuoren polku kuvataan parametrisesti yhtälöllä r(t) = (x(t),y(t)), niin sen derivaatta on r'(t) = (x'(t),y'(t)) ja sen nopeus saadaan yhtälöstä r'(t) = (x'(t),y'(t)) = F(r(t)) = F(x(t),y(t)) =(1,0). Saamme kaksi differentiaaliyhtälöä: x'(t) = 1, josta x(t) = t + C, ja y'(t) = 0, josta y(t) = D. Ajalla t = 0 jäävuori on pisteessä (1,3), joten 0 + C = 1 ja D = 3. Jäävuoren polku on r(t) = (t + 1, 3). Jäävuoren sijainti ajalla t = 7 on r(7) = (8,3).
b) Kenttä on F(x,y)=(2x,y). Mikon piirrustuksen mukaan se näyttää tällaiselta:
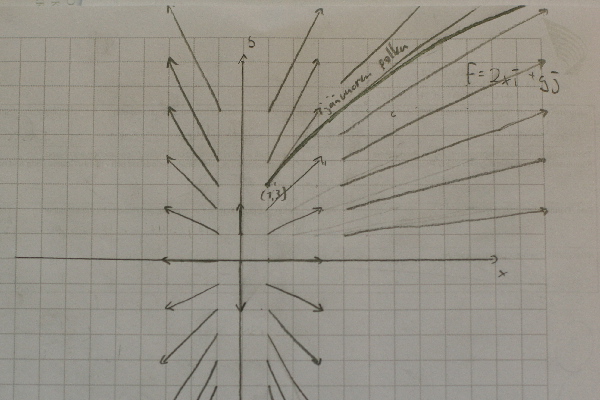
Kuten tapauksessa (a) saamme x'(t) = 2x(t) ja y'(t) = y(t). Yleissivistyksestä tai V1-kurssista muistamme, että on olemassa yksi ainoa funktio, jonka derivaattafunktio on sama kuin funktio itse, nimittäin e-funktio. Eli x(t) = e(2t) + C ja y(t) = e(t) + D. Sijoitamme t=0 ja saamme 1+C = 1 sekä 1+D = 3. Tästä seuraa C = 0 ja D = 2, joten polku on r(t) = (e(2t), e(t)+2). Jäävuoren sijainti ajalla t=7 on r(7) = (e(14), e(7)+2) = (1202604, 1099).
2) (a) Väärin. Analyysin peruslause kahdelle tai useammalle muuttujalle pätee kun F:n paikalla integraalissa on gradF.
(b) Väärin. Kenttä F on gradienttikenttä jos F on polkuriippumaton. Kenttä on polkuriippumaton jos ja vain jos käyräintegraalin arvo pisteestä P pisteeseen Q on sama riippumatta polusta. Tämä tapahtuu jos ja vain jos käyräintegraalin arvo on nolla jokaisella suljetulla käyrällä. Oletuksissa puhuttiin ainoastaan yhdestä suljetusta käyrästä, nimittäin yksikköympyrästä, joten tämä tieto ei riitä.
(c) Oikein. C on suljettu käyrä suunnattu myötäpäivään ja käyräintegraalin arvo C:llä on 3. D on sama käyrä suunnattuna vastapäivään, joten käyräintegraalin arvo D:llä on -3. Kahden kierroksen arvo on -6.
3) (a) Muodostetaan suorakulmion osajoukko D, johon kuuluvat kaikki ne suorakulmion pisteet, joiden molemmat koordinaatit ovat rationaalipisteitä. D:llä on pinta-ala jos sen karakteristinen funktio on integroituva. Onko se? Karakteristinen funktion saa arvon yksi kaikissa D:n pisteissä ja arvon nolla kaikissa muissa. Tarkastellaan suorakulmion ositusta P. Jokaisesta osasuorakulmiosta löytyy piste, jonka koordinaatit ovat rationaalisia, joten alasumma L(karD,P) on nolla. Jokaisesta osasuorakulmiosta löytyy piste, jonka koordinaatit eivät ole rationaalisia, joten yläsumma U(karD,P) on yksi. Riippumatta osituksesta P ala- ja yläsummat saavat arvot nolla ja yksi joten karakteristinen funktion ei ole integroituva eikä D.llä ole pinta-alaa. Olemme käyneet tämän esimerkin läpi monta kertaa luennoilla.
(b) Tarkastellaan funktiota f, jolla on vakioarvo yksi paitsi läpileikkauksen pisteillä. Läpileikkaus on tason nollajoukko, joten se voidaan sivuuttaa integroinnissa ja funktio f on tason vakiofunktiona integroituva. Välin [c,d] läpileikkausfunktion y -> g(p,y) arvo voi olla 1 jos y on rationaalipiste ja 0 muuten. Tällainen läpileikkaus ei ole integroituva välillä [c,d] samasta syystä kuin tapauksessa (a).
Niko ja Thomas tunsivat ratkaisun periaatteet vaikkei ratkaisu ollut heillä täydellinen. Michael väitti ettei suorakulmion sivulla {a<=x<=b, y=c} ole pinta-alaa. Jussi oli samaa mieltä. Emilin mielestä suorakulmion mielivaltaisella pisteellä ei voi olla pinta-ala ja Mikko sanoi samaa suorakulmion kulmapisteistä. Kuitenkin sekä suoralla että pisteellä on tasossa määritelmän mukaan pinta-ala, jonka arvo on nolla.
4) F(x,y,z) = zi
(a) Pinta-ala vektori on muotoa (A,0,0), jossa A on pinnan (positiivinen) pinta-ala, koska pinta on suunnattu x-akselin mukaisesti. Pinnan läpi kulkeva virtaus on muotoa (z,0,0), jossa z on positiivinen. Sisätulo (A,0,0)*(z,0,0) on positiivinen.
(b) Pinta-ala vektori on muotoa (A,0,0), jossa A on pinnan (positiivinen pinta-ala ja pinta on suunnattu x-akselin mukaan. Pinnan läpi kulkeva virtaus on negatiivinen koska z on negatiivinen. Sisätulo (A,0,0)*(z,0,0) on negatiivinen.
(c) Pinta-ala vektori on muotoa (0,0,-A), jossa A on pinta-ala. Pinnan läpi kulkeva virtaus on muotoa (0,0,0) koska pinnalla z on nolla. Sisätulo on nolla.
(d) Pinta-ala vektori on muotoa (0,0,-A), jossa A on pinta-ala. Pinnan läpi kulkeva virtaus on muotoa (z,0,0), jossa z on positiivinen. Sisätulo (0,0,-A)*(z,0,0) on nolla.
(e) Pinta-ala vektori on muotoa (0,A,0), jossa A on positiivinen. Pinnan läpi kulkeva virtaus on muotoa (z,0,0), jossa z on positiivinen. Sisätulo (0,A,0)*(z,0,0) on nolla.
F(x,y,z) = -zi + xk.
(a) Pinta-ala vektori on muotoa (A,0,0), jossa A on pinnan (positiivinen) pinta-ala, koska pinta on suunnattu x-akselin mukaisesti. Pinnan läpi kulkeva virtaus on muotoa (-z,0,0), jossa z on positiivinen. Sisätulo (A,0,0)*(-z,0,0) on negatiivinen.
(b) Pinta-ala vektori on muotoa (A,0,0), jossa A on pinnan (positiivinen pinta-ala ja pinta on suunnattu x-akselin mukaan. Pinnan läpi kulkeva virtaus on muotoa (-(-z), 0, 0), jossa z on positiivinen. Sisätulo (A,0,0)*(-z,0,0) on positiivinen.
(c) Pinta-ala vektori on muotoa (0,0,-A), jossa A on pinta-ala. Pinnan läpi kulkeva virtaus on muotoa (0,0,x), jossa x on positiivinen. Sisätulo (0,0,-A)*(0,0,x) on negatiivinen.
(d) Pinta-ala vektori on muotoa (0,0,-A), jossa A on pinta-ala. Pinnan läpi kulkeva virtaus on muotoa (-z, 0,x), jossa z ja x ovat positiiviset. Sisätulo (0,0,-A)*(-z,0,x) on negatiivinen.
(e) Pinta-ala vektori on muotoa (0,A,0), jossa A on positiivinen. Pinnan läpi kulkeva virtaus on muotoa (-z, 0,x), jossa z ja x ovat positiiviset. Sisätulo (0,A,0)*(-z,0,x) on nolla.
Molemmissa osissa 5 tai 4 oikein antoi 3 pistettä, 2 tai 3 oikein 2 pistettä ja yhdestä oikeasta sai yhden pisteen.