Rinnakkaisoppaana toimii tämä Tarkoitus on yhdistää nämä pikapuoliin yhdeksi kokonaisuudeksi, jonka alku on tässä
addpath /p/edu/mat-1.414/matlab/ addpath /p/edu/mat-1.414/matlab/laode/Jotta näitä ei aina tarvitse toistaa kannattaa kirjoittaa ne oman matlab- hakemiston tiedostoon startup.m
startup.m
%%%%%% Minun omat Matlab-alustukseni addpath /p/edu/mat-1.414/matlab/ addpath /p/edu/mat-1.414/matlab/laode/Tehtävä Tee tämä ja heti!
Toinen tapa on leikkaus/liimaus-tyyli. Samantien voi tehdä työstä html-dokumentin laittamalla kaikki Matlab-koodit ja tulosteet pre-tagien väliin.
Imaginaariyksikkö on i. Jos A ja B ovat reaalisia matriiseja, niin C=A+i*B tuottaa luvuista c(k,l)=a(k,l)+i*b(k,l) koostuvan matriisin. Sekä i että j merkitsevät imaginaariyksikköä. Miten käy loopeissa, joissa esiintyy i tai j? Jos kirjoitetaan ilman kertomerkkiä, niin Matlab hoitaa homman tyylikkäästi:
>> i=-2;z1=3+4*i;
a=
-5
>> b= 3+4i
b=
3.0000 + 4.0000i
Kysymys: Toimiiko myös muuttujasymboleille, käykö muodossa nimi ja inim,
ei varmasti! Mikä neuvoksi esim. for-silmukassa? No ainakin voidaan
tehdä vaikka I=sqrt(-1) ja vapauttaa näin i ja j
silmukkaindekseiksi. (Olis varmaan ollut Matlabissakin viisasta Maplen tavoin
ottaa iso I pienen i:n sijasta.)
Kaikki matemaattiset perusfunktiot toimivat kompleksiargumenteilla myös.
z=a+i*b % a ja b ovat samankokoisia matriiseja
real(z) % reaaliosa(t)
imag(z) % imaginaariosa(t)
laskutoimitukset samat kuin aina: + - * / ^ .* ./ .^
abs(z) % |z|
angle(z) % vaihekulma eli argumentti
conj(z) % liittoluku (a-i*b)
z1=3+4i
plot(real(z1),imag(z1),'*')
xlabel('Reaaliakseli')
ylabel('Imaginaariakseli')
title('z1=3 + 4i')
figure % Uusi kuvaikkuna,
compass(z1) % sinne nuolikuva
Yksittäiselle luvulle voidaan myös komentaa plot(z1);
** Seuraava ei koske harj0:aa **
[BB] s. 186 -> vecrot: Vektorin kierto tasossa. Selkeä ohjelma selityksineen.
Kirjoita, kokeile ja paranna ohjeiden mukaan. Jaetaan ss. 186 - 190
Polynomin määrää kerroinvektori [2,1,5,17] .
kert=[2 1 5 17];
polyval(kert,0)
ans=
17
Polyval on luonnollisesti toteutettu vektorifunktiona, eli voidaan laskea
ja piirtää:
x=linspace(-1,1);y=polyval(kert,x);plot(x,y)
Toki yllä oleva polynomi voidaan laskea myös näin:
x=linspace(-1,1);y=2*x.^3+x.^2+5*x+17;
Tämä on yleisesti ottaen tehoton tapa laskea polynomeja, palataan aiheeseen
myöhemmin. Mikään ei estä tekemästä aikavertailuja ..
Summa- ja erotuspolynomit saadaan suoraan vektoriyhteen-/vähennyslaskulla. Tulo on hieman mutkikkaampi, se olisi sovelias harjoitustehtävä, mutta antaapa nyt olla. Matlabissa on valmis conv, joka sen tekee. Lisäksi polynomijakoon on deconv .
Kokeile vaikka seuraavanlaista:
p=[1 1] % polynomi x+1
p2=conv(p,p)
% Yleisemmin:
pk=p
for k=1:10
pk=conv(p,pk)
end
Tehtäviä
1. Muodosta yllä olevalle polynomille ** ei nyt **Piirretään subplot -funktion avulla p,p' ja p2. Oletetaan, että polynomin kertoimet on sijoitettu muuttujaan kert.p(x)=2x3+x2+5x+17 potenssitp(x)2 jap(x)3 ja piirrä niiden kuvaajat sopivalla välillä. Tarkista Maplella tyyliinp:=2*x^3+...; p2:=expand(p*p); p3:=expand(p*p2); plot(p3,x=-1..1);Katso Matlabin conv-funktion antamia kerroinvektoreita ja vertaa Maplella saatuihin kertoimiin. Voit käyttää Maplessa kaiken kukkuraksi funktiota coeffs.2. Muodosta edellä olevan polynomin derivaattapolynomin kertoimet käyttäen polyder -funktiota.
** ok **
Tarkista Maplella. Piirrä Matlabilla p(x):n ja p'(x):n kuvaajat samaan kuvaan, käytä ihmeessä polyval-funktiota. (Saat piirtää Maplellakin, mutta se on jo liian helppoa.)
3. (** ei **) Kirjoita Matlab-funktio polyint. Voit valita vakiotermin 0:ksi. Mikään ei estä kurkistamasta polyder-toteutusta. Muista: Ei mitään looppiratkaisuja.
function ikert=polyint(c) % Funktio palauttaa c-vektorin määräämän polynomin integraalipolynomin % kerroinvektorin % Kerroinvektorit on järjestetty alenevien potenssien mukaan.
x=linspace(-2,2);
clf
subplot(2,2,1);
plot(x,polyval(kert,x));
xlabel('p(x)');
subplot(2,2,2);
plot(x,polyval(polyder(kert),x));
xlabel('p''(x)');
subplot(2,2,3);
plot(x,polyval(conv(kert,kert),x));
xlabel('p(x)^2');
Tehtävä Lisää edelliseen vielä integraalipolynomin kuva
neljänneksi pikkuruuduksi, käytä tekemääsi polyint-funktiota.
(Voit kokeilla yhtä hyvin joillakin muilla kuin tuolla samalla
polynomilla.)
Olkoon annettu arvovastaavuustaulukko vaikkapa niin, että tasavälisissä pisteissä 1,2,...,10 on annettu y-arvot 1 5 3 3 2 3 6 11 17 34 .
Tehtävänä on sovittaa eriasteisia polynomeja tähän aineistoon. Jos polynomin asteluku on pisteiden lkm - 1, on kyseessä interpolaatiopolynomi, siis kaikkien datapisteidan kautta kulkeva. Jos asteluku on alempi, saadaan kyseisen asteluvun pienimmän neliösumman sovitus. (Näistä puhutaan tarkemmin tuonnempana.)
Kaikkiin näihin tehtäviin soveltuu funktio polyfit
xd=1:10;
yd=[1 5 3 3 2 3 6 11 17 34]
n=length(xd)-1
ipkert=polyfit(xd,yd,n);
pns4kert=polyfit(xd,yd,4);
x=linspace(1,10); %Pisteet,joissa polynomin arvo lasketaan kuvaa varten.
plot(xd,yd,'*',x,polyval(ipkert,x),'b',x,polyval(pns4kert,x),'r')
legend('Datapisteet','Interpolaatiopolynomi','4. asteen PNS-polynomi')
Huomaa, että sovitettava polynomi on syytä laskea tiheässä pisteistössä
( x=linspace(1,10);),
muuten koko hommassa on aika rajoitetusti vitsiä.
?interp
interp - polynomial interpolation
Calling Sequence:
interp( x, y, v )
Parameters:
x - list or vector of independent values, x[1],..x[n+1]
y - list or vector of dependent values, y[1],..y[n+1]
v - variable to be used in polynomial
Edellinen tilanne hoidettaisiin Maplessa näin:
xd:=[seq(i,i=1..10)]: #(tai xd:=[$1..10];) yd:=[1, 5, 3, 3, 2, 3, 6, 11, 17, 34]: p:=interp(xd,yd,t); polykuva:=plot(p,t=0.8..10.2): xyd:=seq([xd[i],yd[i]],i=1..nops(xd)): datakuva:=plot([xyd],style=point,symbol=circle,color=black): plots[display]([polykuva,datakuva]);Tehtävä (** hyvä yes **)
xd=1:10; % xdata
yd=[1 5 3 3 2 3 6 11 17 34] % ydata
x=linspace(0.8,10.2); % Pisteet,joissa polynomin arvo lasketaan.
y=spline(xd,yd,x);
plot(xd,yd,'*r',x,y,'b')
legend('Datapisteet','Interpolaatiopolynomi','4. asteen PNS-polynomi')
grid; shg
Huomataan, että splisovituksen tekninen toteuttaminen on jopa yksinkertaisempaa
kuin polynomi-interpolaation, sillä spline-funktioon on
rakennettu sekä "polyfit"- että "polyval"-tyyppiset toiminnot.
Maplessa toimittaisiin näin:
readlib(spline): xd:=[seq(i,i=1..10)]: #(tai xd:=[$1..10];) yd:=[1, 5, 3, 3, 2, 3, 6, 11, 17, 34]: p:=spline(xd,yd,t); splkuva:=plot(p,t=0.8..10.2): xyd:=seq([xd[i],yd[i]],i=1..nops(xd)): datakuva:=plot([xyd],style=point,symbol=circle,color=black): plots[display]([splkuva,datakuva]);
Tehtäviä1. Tee ankkalintutehtävä tai vast. splinisovituksena.
2. Toteuta Rungen koe sekä polynomi-interp. että splini. Kirjoita funktio runge.m
Aloitetaan yhtälöstä, jota Bombielli tutki n. 500 vuotta sitten.
x3-15x = 4Matlab-istunto:
kert=[1 0 -15 -4];
juuret=roots(kert)
poly(juuret)
Funktio poly on käänteinen funktiolle roots .
Kokeillaanpa lisää, katsotaan, mitä saadaan, jos polynomin juuret ovat -1.
>> juuret=[-1 -1 -1];
>> poly(juuret)
ans=
1 3 3 1
>> juuret=[];
>> for k=1:10;juuret=[juuret,-1];poly(juuret),end;
>> poly(-1*ones(1,10));
Tehtävä
Selvitä, mitä kaikkea yllä olevassa tapahtuu.
Otetaan vielä yksi roots -komennon käyttömahdolisuus. Katsotaan yksikköjuuria, 11/n . Kyseessä on polynomiyhtälön
zn-1=0
ratkaisut.
kert=[1 0 -1] % z2-1
juuret=roots(kert)
plot(juuret)
Yleisemmin:
n=10;
kert=[1,zeros(1,n-1),-1];
z=roots(kert);
plot(re(z),im(z))
Teht. Mitä tästä muistuu mieleen, mitä kaikki tarkoittaa?
helpwin funfun näyttää Matlab-funktioita, joiden argumenttina esiintyy funktio. Esim.
Kuten todettiin, kaikkien nollakohtien määritys on yleensä mahdoton tehtävä, edellä mainitussa esimerkissäkin niitä on kaiken kukkuraksi ääretön määrä. Käytännössä piirrämme kuvaajan, katsomme siitä (mahd. zoom:n avulla) alkuarvauksen ja annamme sen sekä funktiomäärityksen fzero - funktion argumentiksi. Jos käytämme valmiiksi määriteltyä funkiota, niin käyttö on tämännäköistä: fzero('sin',3) antaa varmasti hyvän likiarvon pi:lle
Normaalisti määrittelemme oman funktion, otetaan vaikkapa edellä mainittu yhtälö tan x = x .
%%%%%%%%% tiedosto f.m %%%%%%%%%%%%% function y=f(x) y=x-tan(x); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Testaamme ensin, että funktiomme on kunnossa:
f(0),f(pi/4), f(pi/2)
fplot('f',[0,pi/2-.1])
Nyt voimme kutsua
fzero('f',pi/2-0.1)
Huom! Aina kun käytät "funktifunktiota" ja teet sitä varten
oman funktion, muista testata ensin oma funktiosi . Sitten
vasta saat luvan soveltaa funfunktiota.
Huom! Matlab 5.3:ssa on tällaisten pikkufunktioiden teko tullut mahdolliseksi myös suoraan istunnossa komennolla inline. Otamme siitä tuonnempana esimerkkejä. Joka tapauksessa hiukankin vakavamielisen Matlab-käyttäjän tulee osata sujuvasti myös .m-funktioiden teko.
Tehtävä Kirjoita funktio f(x)=(x-1.96)/(x2+1.15) m-tiedostomääritykseksi, piirrä kuvaaja ja etsi siitä likiarvot minimeille ja nollakohdille. Määritä sitten tarkemmin käyttäen fmin- ja fzero-funktioita.
Muistathan kirjoittaa .m-tiedostosi vektoroidusti. (Mikään ei estä tässä m-tiedostossa käyttämästä myöskään polyval-funktiota, tosin ei se taida kirjoitustyötä säästää.)
feval('sin',x) < -- > sin(x)
feval('f',x1,x2,...,xn) < -- > f(x1,x2,...,xn)
Otetaan oikein yksinkertainen esimerkki. Jospa haluaisimme funfunin, joka
iteroi annettua funktiota f kerran, ts. laskee yhdistetyn funktion
f o f arvoja halutuissa pisteissä.
function y=o(f,x) y=feval(f,feval(f,x));Kutsuesim: o('sin',[1,2,3]) <--> sin(sin([1,2,3]))
Jos käyttäisimme yhtä ja samaa kiinteää funktionnimeä, voisimme kirjoittaa
function y=fof(x) y=f(f(x));Jos nyt haluaisimme tehdä homman sinille, ei auttaisi muu (*) kuin kirjoittaa m-tiedosto f.m:
function y=f(x) y=sin(x)Nyt sitten fof([1 2 3]) antaisi saman sin(sin([1 2 3])):n Rajoituksena olisi, että fof käyttäisi yhtä ja samaa funktiotiedostoa f.m, jota joutuisimme editoimaan, kun haluaisimme käsitellä eri funktioita. Funktio "o" on yleisempi, voimme antaa sille minkänimisen argumentin tahansa.
Muuten, funfun:ia kutsutaan usein matematiikassa operaattoriksi.
Hyödyllisempi ja luonnollisempi esim:
Tehtävä Kirjoita funfun taulukoi:
function Y=taulukoi(f,a,b,h) x=a:h:b; y=feval(f,x); Y=[x' y']No, tehtiin nyt kuitenkin. Kokeile vaikka:
taulukoi('sin',0,pi,0.1)
Tämäkään ei ole varsinainen hyötyfunktio, se vain havainnollistaa
funktion nimen parametrinä välittämistä.
Jokainen tekee nopeammin homman näin:
x=0:0.1,pi;y=sin(x);[x' y'] %% taulukko, taulukointi (find-hakusana)Tämä tarina oli ennen kaikkea siksi, että huomataan, ettei mitään tämän maagisempaa tapahdu Matlabin funfunien sisällä.
(*) Versiossa 5.3 on inline, joka sallisi tämän:
f=inline('sin(x)','x')
>> help logical
LOGICAL Convert numeric values to logical.
LOGICAL(X) returns an array that can be used for logical indexing
or logical tests. Logical arrays are also created by the
relational operators (==,<,>,~, etc.) and functions like ANY, ALL,
ISNAN, ISINF, and ISFINITE.
A(B), where B is a logical array, returns the values of A at the
indices where the real part of B is nonzero (B must be the
same size as A). A(B) is the same as A(FIND(B)).
Most arithmetic operations remove the logicalness from an array.
Seldom necessary, the easiest method is add zero (i.e. A+0).
Matlabissa tämä voidaan ilmaista kätevästi. Ajatellaan, että x on
"diskretoitu x-akseli" ja a ja b skalaareja. Kirjoitetaan:
x > a & x < b
Esim:
>> x=linspace(-1,2);
>> a=0;b=1;
>> Khi=x > a & x < b;
>> Khi([1,2,30,40,50,60,70,90])
ans =
0 0 0 1 1 1 0 0
>> plot(x,Khi)
>> axis([-1 2 -0.1 1.1])
>> grid
>> shg
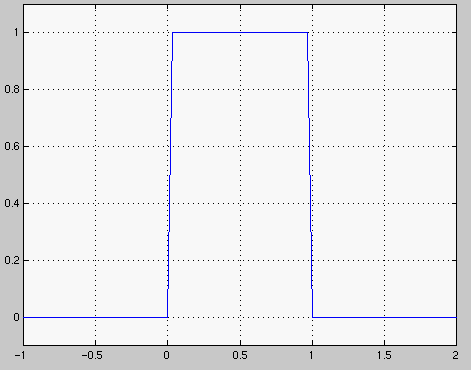
Diskretointivirhe näkyy hyppykohdissa, asia paranruisi kummasti, jos otettaisiin vaikkapa 100 lisäpistettä väleillä (0,h) ja (1-h,1), missä h on diskretointiaskel ( (b-a)/100 ).
Paloittain määritellyt funktiot voidaan kirjoittaa kätevästi (ja vektoroidusti) karakterisististen funktioiden avulla. Tämä ajattelutapa on muutenkin hyödyllinen monissa yhteyksissä matematiikassa. Meillä se tulee vastaan erityisesti V3:ssa Laplace-muunnosten yhteydessä.
1 <= k <= length(v)
Esim:
>> v=floor(10*rand(1,8))
v =
8 4 6 7 9 7 1 4
>> v([1,1,4,8,6,4])
ans =
8 8 7 4 7 7
>> v(0)
??? Index into matrix is negative or zero. See release notes on changes to
logical indices.
>> a=1:10
a =
1 2 3 4 5 6 7 8 9 10
>> a(a<5)
ans =
1 2 3 4
>> a<5
ans =
1 1 1 1 0 0 0 0 0 0
Huomaamme, että indeksointi toimii myös loogisella vektorilla.
>> tosi=a==a
tosi =
1 1 1 1 1 1 1 1 1 1
>> luvut1=ones(size(a))
luvut1 =
1 1 1 1 1 1 1 1 1 1
>> a(tosi)
ans =
1 2 3 4 5 6 7 8 9 10
>> a(luvut1)
ans =
1 1 1 1 1 1 1 1 1 1
>> epatosi=a~=a
epatosi =
0 0 0 0 0 0 0 0 0 0
>> nollat=zeros(size(a))
nollat =
0 0 0 0 0 0 0 0 0 0
>> a(epatosi)
ans =
[]
>> a(nollat)
??? Index into matrix is negative or zero. See release notes on changes to
logical indices.
>> a(logical(nollat)) % komennolla logical muutetaan totuusarvoiksi.
ans =
[]
>> whos
Name Size Bytes Class
a 1x10 80 double array
epatosi 1x10 80 double array (logical)
luvut1 1x10 80 double array
nollat 1x10 80 double array
tosi 1x10 80 double array (logical)
v 1x8 64 double arrayy
Tämä selvitti kaiken, nyt voidaan poimia hyvin kätevästi.
>> a(a>2 & a<7)
ans =
3 4 5 6
>> a(rem(a,2)==0)
ans =
2 4 6 8 10
>> a(rem(a,2)~=0)
ans =
1 3 5 7 9
>> help find
FIND Find indices of nonzero elements.
I = FIND(X) returns the indices of the vector X that are
non-zero. For example, I = FIND(A>100), returns the indices
of A where A is greater than 100. See RELOP.
Tyyppiesimerkki poikkeuspisteen käsittelystä on funktio
f:=x->sin(x)/x;
f(0):=1;
Matlabissa meidän x:mme on pitkä (tavallisesti 100-ulotteinen) vektori,
diskretoitu x-akseli. Kokeillaan kuitenkin lyhyemmällä.
>> x=[-1 -.5 0 .5 1];
>> einollaind=find(x~=0)
einollaind =
1 2 4 5
>> xok=x(einollaind)
xok =
-1.0000 -0.5000 0.5000 1.0000
>> nollaind=find(x==0)
nollaind =
3
Vektori y halutaan määritellä niin, että se saa poikkeuspisteessä arvon 1.
No, voimme alustaa y:n niin, että se saa kaikkialla arvon 1 ja sitten
korjaamme arvot ok-pisteissä, siis einollaind-indekseillä.
>> y=ones(size(x)); % Jos olisi vaikka 5, niin 5*ones(size(x)); >> y(einollaind)=sin(xok)./xok >> plot(x,y)No nyt sitten:
>> x=linspace(-3,3);ein=find(x~=0);
>> y=ones(size(x)); y(ein)=sin(x(ein))./x(ein); plot(x,y)
Helppoahan tämäkin oli, tosin on myönnettävä, että tällä kohden Maple-
ratkaisu tapahtui käden käänteessä ja Matlab-ratkaisuun tarvittiin hieman
useampia käden käänteitä. Varmasti voidaan ratkaista muillakin tavoilla,
vaikkapa jakamalla osavektoreiksi (x<0, x=0, x>0), mutta edellä esitetty
on aika hyvä, vaikka sen itse sanommekin.
>> x=[-1 -.5 0 .5 1]
x =
-1.0000 -0.5000 0 0.5000 1.0000
>> y=sin(x)./x
Warning: Divide by zero.
y =
0.8415 0.9589 NaN 0.9589 0.8415
No nyt ei tarvitse muuta kuin korvata NaN arvolla 1.
>> isnan(y)
ans =
0 0 1 0 0
>> y(ans)=1
y =
0.8415 0.9589 1.0000 0.9589 0.8415
Siten homma hoituu tositilanteessa näinkin:
x=linspace(-3,3); y=sin(x)./x; y(isnan(y))=1;Huomaa, että molemmissa tavoissa homma toimii ilman muutoksia, jos poikkeuspisteitä on useampia edellyttäen, että poikkeusarvot ovat samat. Voit iltojesi iloksi miettiä, miten kätevimmin käsiteltäisiin eri poikkeusarvot. No, jos ilta käy muuten lyhyeksi, niin annetaan vihje
>> x=[-1 -.5 0 .5 1];
>> y=sin(x)./x
y =
0.8415 0.9589 NaN 0.9589 0.8415
>> y(logical([0 1 0 1 0]))
ans =
0.9589 0.9589
>> y(logical([0 1 0 1 0]))=[-2 2]
y =
0.8415 -2.0000 NaN 2.0000 0.8415
Eiköhän tämä aihepiiri tullut aikalailla tyhjentävästi käsitellyksi.
** harj0: voit lopettaa tähän ***
Tähän tarkoitukseen on meshgrid . Kokeillaanpa hiukan
>> x=linspace(-2,2,6), y=linspace(-1,1,3)
x =
-2.0000 -1.2000 -0.4000 0.4000 1.2000 2.0000
y =
-1 0 1
>> [X,Y]=meshgrid(x,y)
X =
-2.0000 -1.2000 -0.4000 0.4000 1.2000 2.0000
-2.0000 -1.2000 -0.4000 0.4000 1.2000 2.0000
-2.0000 -1.2000 -0.4000 0.4000 1.2000 2.0000
Y =
-1 -1 -1 -1 -1 -1
0 0 0 0 0 0
1 1 1 1 1 1
X:ssä on y:n pituuden verran x-rivejä allekkain ja Y:ssä x:n pituuden
verran y-vektoreita vierekkäin. Kun katsotaan matriisien vastinpisteitä
edeten kummassakin matriisissa vaakariveittäin, niin saadaan todellakin
koko hilapisteistö.
Tarkemmin sanottuna matriisit X ja Y yhdessä edustavat solumatriisia:
(x1y1),(x2y1)...(xmy1)
(x1y2),(x2y2)...(xmy2)
...
(x1yn),(x2yn)...(xmyn)
Tällainen solumatriisi voidaan nykyversioilla (versiosta 5 alkaen)
luoda, mutta sitä ei tavallisesti tarvita. (Ennenhän se ei edes ollut
mahdollinen.) Jos ajattelemme 3d grafiikkaa, tarvitaan funktion arvot
hilapisteissä. Ne saadaan soveltamalla vektoroidusti määriteltyä
funktiota f matriiseihin X ja Y, siis Z=f(X,Y).
>> Xt=X';Yt=Y';
>> [Xt(:),Yt(:)]
ans =
-2.0000 -1.0000
-1.2000 -1.0000
-0.4000 -1.0000
0.4000 -1.0000
1.2000 -1.0000
2.0000 -1.0000
-2.0000 0
-1.2000 0
-0.4000 0
0.4000 0
1.2000 0
2.0000 0
-2.0000 1.0000
-1.2000 1.0000
-0.4000 1.0000
0.4000 1.0000
1.2000 1.0000
2.0000 1.0000
>> plot(Xt(:),Yt(:),'x')
>> axis([-2.5 2.5 -1.2 1.2 ])
>> grid
Otetaan "perus-kahden muuttujan funktio"
f(x,y)=xy
Korkeusmatriisimme syntyy yksinkertaisesti näin
>> Z=X.*Y % Tositilanteessa puolipiste. >> figure >> mesh(x,y,Z) >> hold on ; plot(Xt(:),Yt(:),'x') >> surfc(x,y,Z) >> colormap(cool) >> colorbar
clf
m=30;n=20;
x=linspace(-2,2,m); y=linspace(-1,1,n);
[X,Y]=meshgrid(x,y);
%Z=X.*Y; % No kuka tuotakaan jaksaiai aina katsella
% Yleisesti tyyliin:
f=inline('x.^2-y.^3+sin(x).*cos(y)','x','y');
Z=f(X,Y);
% mesh(x,y,Z) % rautalankakuva (joskus havainnollinen)
surfc(x,y,Z)
colormap(winter)
colorbar
shg
Piirretään vielä hilapisteitä pinnalle ja/tai pohjatasolle:
hold on %plot3(X(:),Y(:),Z(:),'o') plot3(X(:),Y(:),-2*ones(size(X(:))),'r.')
x=linspace(-2,2,6), y=linspace(-1,1,3)
[X,Y]=meshgrid(x,y)
for i=1:6 % Luodaan solumatriisi, jonka
for j=1:3 % alkioina on 2:n pituiset vektorit
XY{i,j}=[x(i),y(j)]; % [x(i),y(j)];
end
end
XY=XY' % Transponoidaan, sillä meshgrid:n
cellplot(XY) % vaaka-akseli on x-akseli ja pysty y.
%g=inline('x(1).*x(2)','x');
XY{1,:} % Katsotaan solumatriisin 1. rivi
XY2(:,:,1)=X; XY2(:,:,2)=Y; % Kootaan X- ja Y-"tasot" 3-ulotteiseksi
XY2 % matriisiksi
Tässä yhteydessä solumatriisista ja 3-ulotteisesta matriisista ei
liene muuta kuin ajatuksellinen
hyöty. Samalla opimme näiden uusien tietorakenteiden käsittelyn perusteita.
>> coeff=polyfit(xdata,ydata,n); x=linspace(a,b);y=polyval(coeff,x); >> ys=spline(xdata,ydata,xev);
% Assume our function is known at some data points. (By for eg. FD or FEM- % calculation). % How do we evaluate it in intermediate points? [x,y]=meshgrid(-3:3); z=peaks(x,y); surf(x,y,z) [xi,yi]=meshgrid(-3:0.5:3); figure zi=interp2(x,y,z,xi,yi); % nearest, bilinear surf(xi,yi,zi) zi=interp2(x,y,z,xi,yi,'bicubic'); surf(xi,yi,zi) % We may also want to go in the reverse direction. We may have done a very % accurate computation, but there's no point using the mesh- or surf-functions % for a very dense data. (It takes very long and the result doesn't look good.) % Also, we may want to evaluate the error at certain data points that are a % subset of the computed values. % % Fine, it works both ways: zii=interp2(xi,yi,zi,x,y); surf(x,y,zii) % Our original "peaks".See also:
DELAUNAY,VORONOI, TRIMESH, TRISURF, GRIDDATA, CONVHULL, DSEARCH, TSEARCH
u(x,t)=sin(pi t)sin(pi x).
Cooper s. 496.
>> nframes=20
>> x=0:0.1:10;
>> moviein(nframes);
for j=1:nframes;
t=(j-1)*.1
u=sin(pi*t)*sin(pi*x);
plot(x,u)
M(:,j)=getframe;
end;
Nämä komennot luovat matriisin M, johon elokuva on talletettu.
Nyt voidaan elokuva ajaa esim. komennolla
>> movie(M,4,10);Tämä tarkoittaa: Aja elokuva 4 kertaa nopeudella 10 kehystä sekunnissa.
Tehdään luennolla 1.3.2000 esitetyn mukaisesti ensin.
clear
N=10;
%function y=g(x)
% BF s. 54 Teht. 1
%y=polyval([-2 1 3],x).^(1/4);
% Voidaan määritellä nykyisin myös istunnossa suoraan:
g=inline('polyval([-2 1 3],x).^(1/4)','x');
a=0;b=1.5;x0=(a+b)/2; % Alkupisteeksi välin keskipiste.
x(1)=g(x0);
for i=1:N-1;
x(i+1)=g(x(i));
end;
x2apu=[x(1:N-1);x(1:N-1)]; % x(1),x(2),x(3) jos N=4
% x(1),x(2),x(3)
xx=x2apu(:); % Jonoutus sarakkeittain tekee kahdennuksen.
xpisteet=[x0,xx'];ypisteet=[xx',x(N)];
% Tyylipuhdas, selkeä, kaunis!
% No piirretään.
clf
fplot('g',[a b])
hold on
plot([a b],[a b])
plot(xpisteet,ypisteet,'r')
grid
shg
xlim([0.5 1.4]) % Riippuu g:stä
ylim([0.6 1.4]) % Riippuu g:stä
x
diff(x) % Kätevä funktio, muodostaa x-vektorin alkioiden erotukset.
% Nähdään suoraan, onko kiintopisteominaisuus jo lähellä.
format long
format short
% Voidaan toki toteuttaa helposti myös for-silmukalla. Tällöin voidaan
% samantien tehdä vuorovaikutteiseksi
clf
fplot('g',[a b])
hold on
plot([a b],[a b])
grid
shg
a=0;b=1.5;x0=(a+b)/2;
plot([x0],[g(x0)])
x(1)=g(x0);
for i=1:N-1;
x(i+1)=g(x(i));
plot(x([i,i,i+1]),x([i,i+1,i+1]),'r')
display('Paina ENTER');
pause;
end;
# Iteraatiot
# Työarkista Lv7iter.mws
# Kiintopisteiteraatio
# Cobweb: (Robert Israelin tapaan)
porras:=x->plot([[x,x],[x,f(x)],[f(x),f(x)]]): # Annetaan f:n olla globaali.
# KRE EXA 1 s. 926-927
#
g1:=x->(1/3)*(x^2+1);
plot([x,g1(x)],x=0..5);
X:='X':f:='f':
f:=g1:
X[0]:=1.0:
n:=10:
for i to n do X[i]:=g1(X[i-1]) od:
fjaxkuva:=plot([x,f(x)],x=0 .. 1,color=[blue,black]):
with(plots):
display({fjaxkuva,seq(porras(X[i]),i=0..n)});
xd=0:2:10;yd=sin(xd); n=length(xd); x=linspace(0,10);clf y=spline(xd,yd,x);plot(x,y);hold on;plot(xd,yd,'or');grid;shg %[xd,yd]=ginput(n); y=spline(xd,yd,x);plot(x,y); plot(xd,yd,'or');shg % Tässä valitaan hiirellä samanverran pisteitä kuin on alkup. solmuja. [xd,yd]=ginput; y=spline(xd,yd,x);plot(x,y); plot(xd,yd,'or');shg % Tässä valitaan siihen saakka, kunnes huvittaa painaa grafiikkaikkunassa ENTER:iä.Tällaista vuorovaikutteista tapaa on erityisen soveliasta kokeilla Bezier- käyrien yhteydessä.
1+x2-y2+excos y = 0 2 x y + ex sin y = 0Piirretään ensin:
clf
x=linspace(-2,5,40);y=linspace(-6,6,40);
[X,Y]=meshgrid(x,y);
Z1=1+X.^2-Y.^2+exp(X).*cos(Y);
Z2=2*X.*Y+exp(X).*sin(Y);
contour(X,Y,Z1,[0 0]) % Piirretäessä vain yksi korkeuskäyrä, pitää antaa
hold on % korkeusvektori, jossa 2 samaa arvoa. ("feature")
contour(X,Y,Z2,[0 0],'r')
grid
shg
figure
surfl(X,Y,Z1);hold on; surfc(X,Y,Z2);colorbar;shg;grid
%%%%%%% funjac.m %%%%%%%%%%%%
function [f,J]=funjac(x)
% Kutsuesim: [f,J]=funjac([1,2]) % Lasketaan funktio ja Jakobiaani pist [1,2].
% Tämä on algoritmin ongelmariippuva osa, käytä tarvittaessa Maplea
% Jakobiaanin muodostamiseen
function [f,J]=funjac(xy)
% Kutsuesim: [f,J]=funjac([1,2]) % Lasketaan funktio ja Jakobiaani pist [1,2].
% Tämä on algoritmin ongelmariippuva osa, käytä tarvittaessa Maplea
% Jakobiaanin muodostamiseen
x=xy(1);y=xy(2); % Tämä vain alla olevan kaavan helppolukuis/kirjoittamiseksi
f=[1+x^2-y^2+exp(x)*cos(y); 2*x*y+exp(x)*sin(y)];
J=[2*x + exp(x)*cos(y), -2*y - exp(x)*sin(y)
2*y + exp(x)*sin(y), 2*x + exp(x)*cos(y)];
%%%%%%%%% end funjac.m %%%%%%%%%%%%%%%%%%%%%%%%%
\ MAPLE / reserved. Maple and Maple V are registered trademarks of
<____ ____> Waterloo Maple Inc.
| Type ? for help.
> with(linalg):
> jacobian([1+x^2-y^2+exp(x)*cos(y),2*x*y+exp(x)*sin(y)],[x,y]);
[2 x + exp(x) cos(y) -2 y - exp(x) sin(y)]
[ ]
[2 y + exp(x) sin(y) 2 x + exp(x) cos(y) ]
Sitten iteroidaan:
x=[1;-2]; [fx,Jx]=funjac(x);h=-Jx\fx;x=x+h Tai vaikka: figure(1) % Palataan korkeuskäyräkuvaikkunaan. x=ginput(1) % Valitaan hiirellä yksi piste korkeuskäyräkuvasta. x=x' [fx,Jx]=funjac(x);h=-Jx\fx;x=x+h
x=-2:.2:2;y=-1:.15:1;
[X,Y] = meshgrid(x,y);
f=inline('x .* exp(-x.^2 - y.^2)','x','y');
Z=f(X,Y); [px,py] = gradient(Z,.2,.15);
contour(X,Y,Z), hold on
quiver(X,Y,px,py), hold off, axis image
|