 Mat-1.312 Matematiikan peruskurssi T2 / kevat 1996
Mat-1.312 Matematiikan peruskurssi T2 / kevat 1996
Viviani'n ikkuna
 Varmuuden vuoksi: Poistetaan mahdolliset aiemmat muuttujat:
Varmuuden vuoksi: Poistetaan mahdolliset aiemmat muuttujat:
Input :=
Remove["Global`*"]
 Ladataan vektoritulo:
Ladataan vektoritulo:
Input :=
<<LinearAlgebra`CrossProduct`
Input :=
?Cross
Cross[vec1, vec2] gives the vector product of the 3-vectors
vec1 and vec2.
Input :=
 Tapa 1: Pallopinnan parametrisointi xy-tason napakoordinaateilla
Tapa 1: Pallopinnan parametrisointi xy-tason napakoordinaateilla
 Parametrisointi:
Parametrisointi:
Input :=
x= r Cos[phi]; y= r Sin[phi];
z= Sqrt[R^2-x^2-y^2]//Simplify;
 Pintaintegraalin pinta-alkion laskeminen (piste on skalaaritulon merkki; komennon loppuun voidaan panna lisamaare //Simplify, mika vastaa taysin seuraavalla rivilla
Pintaintegraalin pinta-alkion laskeminen (piste on skalaaritulon merkki; komennon loppuun voidaan panna lisamaare //Simplify, mika vastaa taysin seuraavalla rivilla
annettavaa komentoa Simplify[%]):
Input :=
p= Cross[D[{x,y,z},r],D[{x,y,z},phi]]//Simplify
Output =
2 2
r Cos[phi] r Sin[phi]
{--------------, --------------, r}
2 2 2 2
Sqrt[-r + R ] Sqrt[-r + R ]
Input :=
dS= Sqrt[p.p]//Simplify
Output =
2 2
r R
Sqrt[--------]
2 2
-r + R
 Tarvitaan lisasievennys (miksi?):
Tarvitaan lisasievennys (miksi?):
Input :=
dS= PowerExpand[dS]
Output =
r R
--------------
2 2
Sqrt[-r + R ]
 Pintaintegraalin laskeminen:
Pintaintegraalin laskeminen:
Input :=
Integrate[dS,{phi,-Pi/2,Pi/2},{r,0,R Cos[phi]}]
Output =
2 2
-2 R Sqrt[R ] + Pi R Sqrt[R ]
Input :=
%//PowerExpand
Output =
2 2
-2 R + Pi R
Input :=
 Tapa 2: Pallopinnan parametrisointi (R/2,0)-keskisilla napakoordinaateilla
Tapa 2: Pallopinnan parametrisointi (R/2,0)-keskisilla napakoordinaateilla
 Parametrisointi:
Parametrisointi:
Input :=
x= (R/2) + r Cos[phi]; y= r Sin[phi];
z= Sqrt[R^2-x^2-y^2]//Simplify;
 Pinta-alkion laskeminen:
Pinta-alkion laskeminen:
Input :=
p= Cross[D[{x,y,z},r],D[{x,y,z},phi]]//Simplify
Output =
r (R + 2 r Cos[phi])
{-----------------------------------,
2 2
Sqrt[-4 r + 3 R - 4 r R Cos[phi]]
2
2 r Sin[phi]
-----------------------------------, r}
2 2
Sqrt[-4 r + 3 R - 4 r R Cos[phi]]
Input :=
dS= Sqrt[p.p]//Simplify//PowerExpand
Output =
2 r R
-----------------------------------
2 2
Sqrt[-4 r + 3 R - 4 r R Cos[phi]]
 Integrointi (tama johtaa raskaanpuoleiseen laskentaan; ala aktivoi solua, jos koneissa on kova kuormitus):
Integrointi (tama johtaa raskaanpuoleiseen laskentaan; ala aktivoi solua, jos koneissa on kova kuormitus):
Input :=
Integrate[dS,{r,0,R/2},{phi,-Pi,Pi}]
Output =
2 2
r R 2 2
2 R Integrate[r ((2 Sqrt[--------------] Sqrt[-4 r + 3 R ]
2 2 2
(4 r - 3 R )
-8 r R
EllipticK[--------------------]) /
2 2
-4 r - 4 r R + 3 R
4 r R
(r R Sqrt[1 - ------------]) +
2 2
-4 r + 3 R
2 2
r R 2 2
(2 Sqrt[--------------] Sqrt[-4 r + 3 R ]
2 2 2
(4 r - 3 R )
8 r R
EllipticK[--------------------]) /
2 2
-4 r + 4 r R + 3 R
4 r R R
(r R Sqrt[1 + ------------])), {r, 0, -}]
2 2 2
-4 r + 3 R
 Integrointi symbolisesti ei onnistu (ainakaan silla versiolla 2.2 / PC-Windows,
Integrointi symbolisesti ei onnistu (ainakaan silla versiolla 2.2 / PC-Windows,
jolla muistilehtio (Notebook) on tehty), joten tehdaan numeerisesti:
Input :=
NIntegrate[dS/.R->1,{r,0,(R/2)/.R->1},{phi,-Pi,Pi}]
NIntegrate::slwcon:
Numerical integration converging too slowly; suspect one of
the following: singularity, oscillatory integrand, or
insufficient WorkingPrecision.
NIntegrate::slwcon:
Numerical integration converging too slowly; suspect one of
the following: singularity, oscillatory integrand, or
insufficient WorkingPrecision.
NIntegrate::slwcon:
Numerical integration converging too slowly; suspect one of
the following: singularity, oscillatory integrand, or
insufficient WorkingPrecision.
General::stop:
Further output of NIntegrate::slwcon
will be suppressed during this calculation.
Output =
1.14159
 Onko tulos sama kuin tavassa 1 ?
Onko tulos sama kuin tavassa 1 ?
Input :=
(Pi-2)*R^2 /. R->1 //N
Output =
1.14159
 Kuva
Kuva
 Pallon ja lierion parametrisoinnit:
Pallon ja lierion parametrisoinnit:
Input :=
pallo= {Sin[th]Cos[phi],Sin[th]Sin[phi],Cos[th]}
Output =
{Cos[phi] Sin[th], Sin[phi] Sin[th], Cos[th]}
Input :=
lierio= {1/2+1/2 Cos[phi],1/2 Sin[phi],h}
Output =
1 Cos[phi] Sin[phi]
{- + --------, --------, h}
2 2 2
 Kuvat:
Kuvat:
Input :=
pallonkuva= ParametricPlot3D[pallo,
{th,0,Pi},{phi,-Pi,Pi},DisplayFunction->Identity]
ParametricPlot3D::ppcom:
Function pallo cannot be compiled; plotting will proceed
with the uncompiled function.
Output =
-Graphics3D-
Input :=
lierionkuva= ParametricPlot3D[lierio,
{phi,-Pi,Pi},{h,-1,1},DisplayFunction->Identity]
ParametricPlot3D::ppcom:
Function lierio cannot be compiled; plotting will proceed
with the uncompiled function.
Output =
-Graphics3D-
Input :=
Show[pallonkuva,lierionkuva,
DisplayFunction->$DisplayFunction]
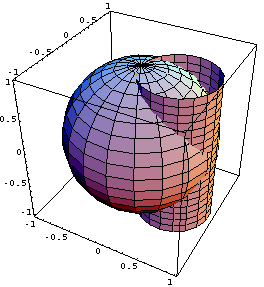
Output =
-Graphics3D-
Input :=
Show[%,ViewPoint->{3,-0.5,2}]
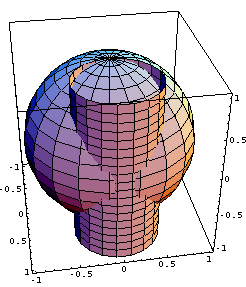
Output =
-Graphics3D-
 Minkamuotoinen pallon ja lierion leikkauskayra oikeastaan on? Sivuavatko pallo ja lierio toisiaan?
Minkamuotoinen pallon ja lierion leikkauskayra oikeastaan on? Sivuavatko pallo ja lierio toisiaan?

