Alkuviikko 8, demo 127
Alkuviikko 8, demo 127
Input :=
f={(4-u Sin[v])Cos[2v], (4-u Sin[v])Sin[2v], u Cos[v]}
Output =
{Cos[2 v] (4 - u Sin[v]), (4 - u Sin[v]) Sin[2 v], u Cos[v]}
Input :=
ParametricPlot3D[f,{u,-1,1},{v,0,Pi},PlotPoints->{2,36}]
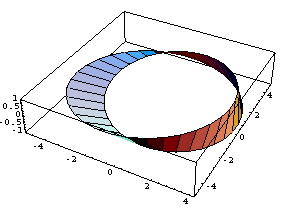
Output =
-Graphics3D-
Input :=
<<LinearAlgebra`CrossProduct`
Input :=
n=Simplify[Cross[D[f,u],D[f,v]]]
Output =
{Cos[v] (-8 Cos[2 v] + u Sin[v] + u Sin[3 v]),
u u Cos[4 v]
- - u Cos[2 v] - ---------- - 4 Sin[v] - 4 Sin[3 v],
2 2
2 Sin[v] (-4 + u Sin[v])}
Input :=
{nx,ny,nz}=n;
Input :=
kulma=ArcTan[ nz/Sqrt[nx^2+ny^2] ]
Output =
ArcTan[(2 Sin[v] (-4 + u Sin[v])) /
u u Cos[4 v]
Sqrt[(- - u Cos[2 v] - ---------- - 4 Sin[v] - 4 Sin[3 v])
2 2
2 2 2
+ Cos[v] (-8 Cos[2 v] + u Sin[v] + u Sin[3 v]) ]]
Input :=
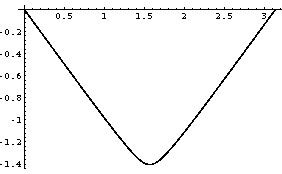
Plot[kulma /. u->1, {v,0,Pi}];
Input :=
<<Graphics`PlotField3D`
Input :=
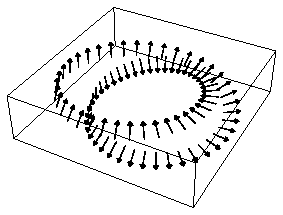
ListPlotVectorField3D[Table[{f,n},{v,0,Pi,Pi/32}] /. u->1,
ScaleFunction->(0.9&),VectorHeads->True];
Input :=
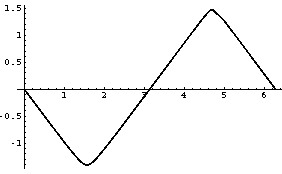
Plot[kulma /. u->1, {v,0,2Pi}];
Input :=
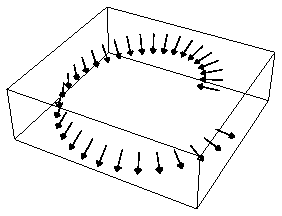
ListPlotVectorField3D[Table[{f,n},{v,0,2Pi,Pi/40}] /. u->1,
ScaleFunction->(0.9&),VectorHeads->True];