Contents
% matlab/lampo/CRNich.m Luento 5.12.08 % Crank-Nicholson'n menetelmä lämpöyhtälölle % Implisiittinen menetelmä, absoluuttisesti stabiili % Esim. 1 KRE ss. 976-978 % clear; close all x=0:0.2:1 n=length(x) % Osavälien lkm. u0=sin(pi*x)' % Alkuarvot vektoriin u0 u0s=u0(2:n-1) % Sisäsolmuarvot %A=4*eye(n-1)+diag(-1*ones(n-2,1),-1)+diag(-1*ones(n-2,1),1) % Tehokkampaa ja helpompi kirjoittaa spdiags:lla: e=ones(n-2,1); A=spdiags([-e 4*e -e],-1:1,n-2,n-2); KatsotaanAtaysi=full(A) B=spdiags([e e],[-1 1],4,4); KatsotaanBtaysi=full(B) % 1. aika-askel j:0->1 % Tässä olis vähemmän elegantti, vaikeammin yleistyvä tapa: % u0=sin(pi*x)'; b=[u0(3);u0(2)+u0(4);u0(3)+u0(5);u0(4)]; % Täsä se elegantti (vrt. luennot) b=B*u0s u1s=A\b; u1=[0;u1s;0] % 1. aikataso vektorissa u1 t=k=0.04 U=[u0 u1]'
x =
0 0.2000 0.4000 0.6000 0.8000 1.0000
n =
6
u0 =
0
0.5878
0.9511
0.9511
0.5878
0.0000
u0s =
0.5878
0.9511
0.9511
0.5878
KatsotaanAtaysi =
4 -1 0 0
-1 4 -1 0
0 -1 4 -1
0 0 -1 4
KatsotaanBtaysi =
0 1 0 0
1 0 1 0
0 1 0 1
0 0 1 0
b =
0.9511
1.5388
1.5388
0.9511
u1 =
0
0.3993
0.6460
0.6460
0.3993
0
U =
0 0.5878 0.9511 0.9511 0.5878 0.0000
0 0.3993 0.6460 0.6460 0.3993 0
2. aika-askel j:1->2
%b=[u1(3);u1(2)+u1(4);u1(3)+u1(5);u1(4)] b=B*u1s u2s=A\b; u2=[0;u2s;0] % 2. aikataso vektorissa u2 t=2*k=0.08 U=[u0 u1 u2]'
b =
0.6460
1.0453
1.0453
0.6460
u2 =
0
0.2712
0.4388
0.4388
0.2712
0
U =
0 0.5878 0.9511 0.9511 0.5878 0.0000
0 0.3993 0.6460 0.6460 0.3993 0
0 0.2712 0.4388 0.4388 0.2712 0
3. aika-askel j:2->3
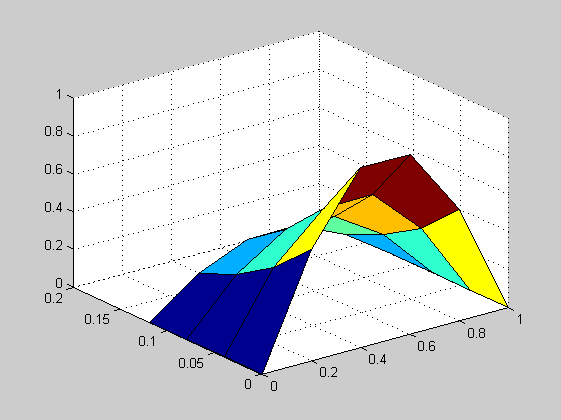
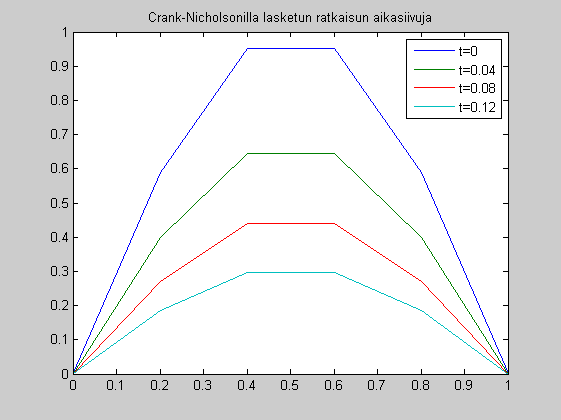
b=B*u2s u3s=A\b; u3=[0;u3s;0]; % 3. aikataso vektorissa u3 t=3*k=0.12 U=[u0 u1 u2 u3]' t=0:0.04:0.12 surf(x,t,U) figure plot(x,U) legend('t=0','t=0.04','t=0.08','t=0.12') title('Crank-Nicholsonilla lasketun ratkaisun aikasiivuja') % Verrataan tarkkaan ratkaisuun u(x,t)= sin(pi*x)*exp(-pi^2*t) % Tehdään vasta ensi viikolla.
b =
0.4388
0.7101
0.7101
0.4388
U =
0 0.5878 0.9511 0.9511 0.5878 0.0000
0 0.3993 0.6460 0.6460 0.3993 0
0 0.2712 0.4388 0.4388 0.2712 0
0 0.1842 0.2981 0.2981 0.1842 0
t =
0 0.0400 0.0800 0.1200