Contents

% ratk4tietok.m
% Lineaarinen 2 x 2- systeemi, diagonalisoituva matriisi
% close all

Määrittele matriisi A tehtävän harj 4 AV mukaisesti.

A=[1/3 4/3;8/3 5/3]

A =

    0.3333    1.3333
    2.6667    1.6667

Muodosta matriisi X, jonka sarakkeina ovat ominaisvektorit ja

matriisi D, jonka lävistäjällä vastaavat ominaisarvot.

[X,D]=eig(A);

Muodosta vektori d, jossa on D:n lävistäjä.

d=diag(D)

d =

   -1.0000
    3.0000

Kirjoita yleinen ratkaisukaava tähän tyyliin:

C(1)=1; C(2) = 1; % sama kuin C=[1 1];
t=0.2;
 Y=C(1)*exp(d(1)*t)*X(:,1) + C(2)*exp(d(2)*t)*X(:,2)

Y =

   -1.3938
   -1.0508

Ratkaise vakiot C alkuarvojen avulla tyyliin:

Y0=[1;0]   % Muuteltava alkuarvo
C= X\Y0    % Ratkaise yhtälöryhmä  % C=M\b, missä M=xxx ja b=xxx.

Y0 =

     1
     0


C =

   -0.9428
   -0.7454

Nyt haluaisit piirtää ratkaisun aikakuvan ja ennenkaikkea faasikuvan.

Mutta voi, eihän se tuosta Y:n lausekkeesta onnistu, siihen ei saa mitenkään järkevästi t:n paikalle t-vektoria. hm - hm - hm

Mikä se juttu olikaan, joka on mainittu luennolla 27 kertaa?
Lineaarikombinaatiot matriisitulona, riviajattelu vs. sarakeajattelu:
Y = X*[C(1)*exp(d(1)*t);C(2)*exp(d(2)*t)]  % Kokeile, saatko saman kuin
yllä, kun t:llä on edellä annettu skalaariarvo.
Jälkimmäisen muodon suuri etu on tässä se, että kerrottavia vektoreita
voi olla paljon, ne kootaan 2-riviseksi matriisiksi, ja homma hoituu yhdellä
matriisitulolla.

Nyt tositoimiin!

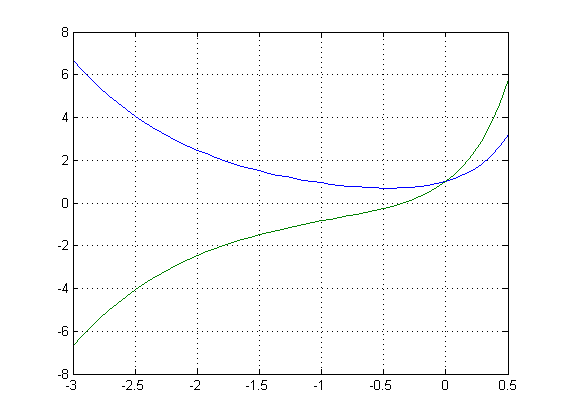
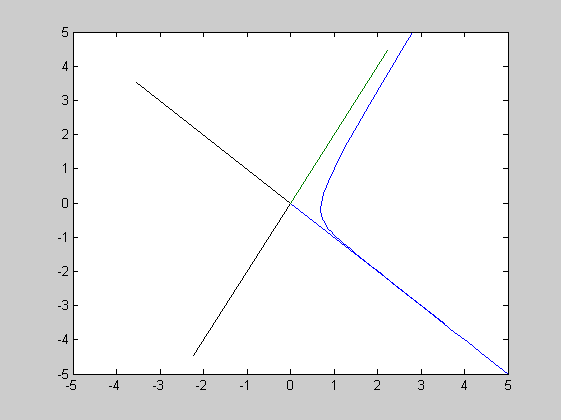
Y0=[1;1]; C=X\Y0;
t=linspace(-3,0.5,50);
Y = X*[C(1)*exp(d(1)*t);C(2)*exp(d(2)*t)];
Y(:,1:10)   % Katsotaan 10 ekaa pistettä.
 plot(t,Y(1,:),t,Y(2,:)); grid on; shg  % Aikakuva
 figure   % seuraava ikkuna
 plot(Y(1,:),Y(2,:))  % Faasikuva
 axis([-5 5 -5 5])  % Sama koordinaatisto kuin pplanessa.
% Miten piirretään ominaissuorat? Nehän ovat sarakkeina matriisissa X.
hold on
plot(5*[0 X(1,1)],5*[0,X(2,1)],'k',5*[0,X(1,2)],5*[0,X(2,2)],'k')
plot(-5*[0 X(1,1)],-5*[0,X(2,1)],-5*[0,X(1,2)],-5*[0,X(2,2)]) % Myös vastavektorit

ans =

  Columns 1 through 6

    6.6953    6.2337    5.8040    5.4040    5.0315    4.6847
   -6.6950   -6.2334   -5.8037   -5.4035   -5.0309   -4.6840

  Columns 7 through 10

    4.3618    4.0612    3.7813    3.5208
   -4.3609   -4.0601   -3.7800   -3.5191

Olispa hauskaa, jos voitaisiin piirtää suuntakenttä ja siinä valita

alkupiste hiirellä, kuten Java-pplane:ssa.
No näin vähäisellä koodilla se käy tässä:

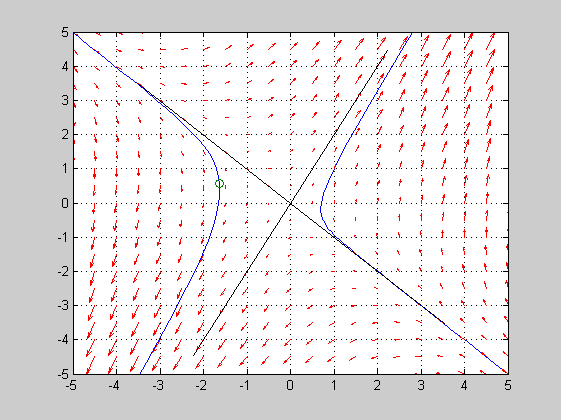
[y1,y2]=meshgrid(-5:0.5:5,-5:0.5:5); % Koordinaattihilapisteistö
dy1=A(1,1)*y1+A(1,2)*y2; dy2=A(2,1)*y1+A(2,2)*y2;  % Derivaattavektori
% saadaan lineaariselle näin: dy=A*y, jos y on jokin 2 x 1-vektori.
% Tässä on kirjoitettava matriisitulo auki, koska y1 ja y2 ovat
% hilapisteistön määrääviä matriiseja, joten dy=A*[y1;y2] on "mahdoton yhtälö".
% clf  % Puhdistetaan ikkuna 2.
quiver(y1,y2,dy1,dy2) % Suuntanuolet hilapisteisiin derivaattojen suuntaan.
axis([-5 5 -5 5]); grid on;hold on
plot(5*[0 X(1,1)],5*[0,X(2,1)],'k',5*[0,X(1,2)],5*[0,X(2,2)],'k')
plot(-5*[0 X(1,1)],-5*[0,X(2,1)],'k',-5*[0,X(1,2)],-5*[0,X(2,2)],'k')
disp('Kuljeta hiirtä grafiikkaikkunaan ja klikkaa')
Y0=ginput(1)'; % Matlab antaa hiusristikon, jonka avulla voit hiirellä valita
                % alkupisteen.
C=X\Y0;        % Ratkaise vakiot.
t=linspace(-3,1,50);   % Kokeile eri arvoja
Y = X*[C(1)*exp(d(1)*t);C(2)*exp(d(2)*t)];
plot(Y(1,:),Y(2,:),Y0(1),Y0(2),'o')    % Faasikuva ja alkuarvopiste
%axis([-5 5 -5 5]); grid on; shg

Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

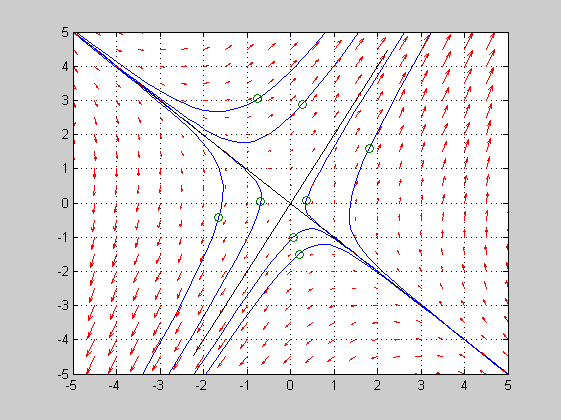
%Talletetaan viimeinen kappale tiedostoon ratk4ajo.m
%Voit ajaa komennot komentamalla Matlab-ikkunassa:

close all    % grafiikkaruutujen poisto
%ratk4ajo
% Usempia trajektoreita:
%close all
%ratk4ajo;ratk4ajo;ratk4ajo
% tai:
close all
n=8;
for i=1:n
    disp(['Sinulla on ',num2str(n-i+1),' klikkaus(ta)'])
    ratk4ajo
 end

Sinulla on 8 klikkaus(ta)
Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

C =

    2.1464
   -1.7193

Sinulla on 7 klikkaus(ta)
Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

C =

    1.1079
   -2.3442

Sinulla on 6 klikkaus(ta)
Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

C =

   -0.9541
   -2.5359

Sinulla on 5 klikkaus(ta)
Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

C =

   -0.8945
    0.9764

Sinulla on 4 klikkaus(ta)
Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

C =

    1.3534
    1.5440

Sinulla on 3 klikkaus(ta)
Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

C =

    0.6615
    0.4739

Sinulla on 2 klikkaus(ta)
Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

C =

   -0.3023
   -0.3207

Sinulla on 1 klikkaus(ta)
Kuljeta hiirtä grafiikkaikkunaan ja klikkaa

C =

   -0.5298
    0.7090

Published with MATLAB® 7.6