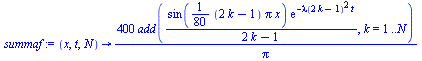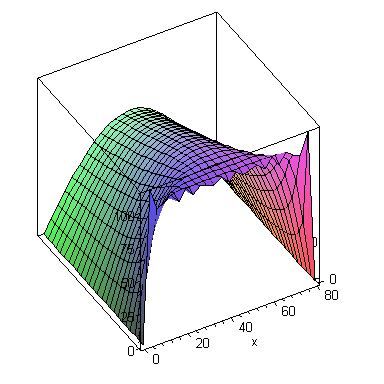Lämpöyhtälö muuttujat erotellen
KP3-II 9.12.2008
Alustukset
| > |
with(plots): setoptions3d(orientation=[-120,50],axes=box): |
Esim
KRE s. 603 Exa 1
| > |
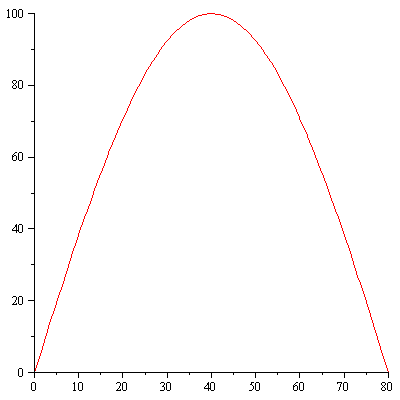
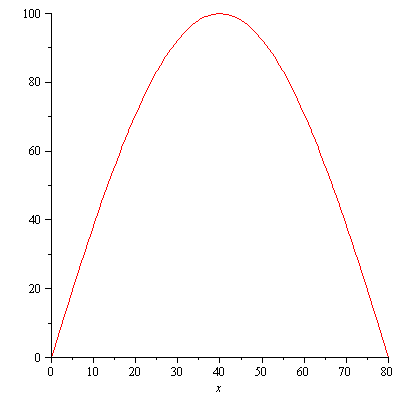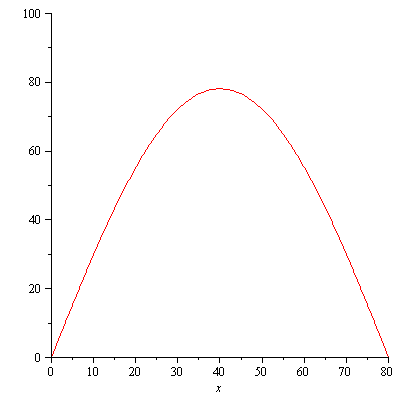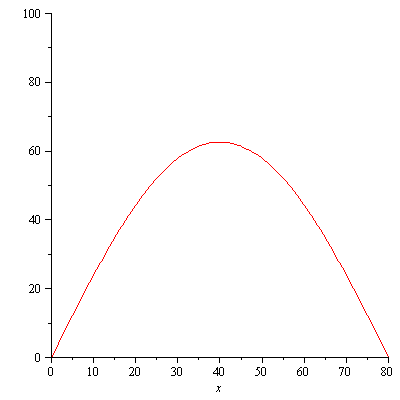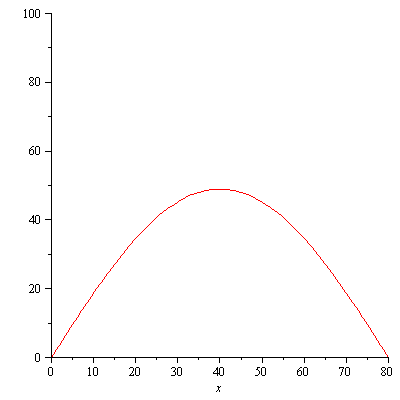
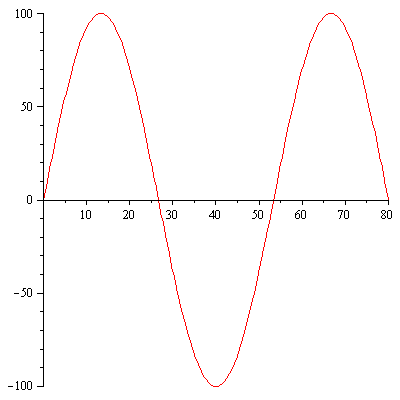
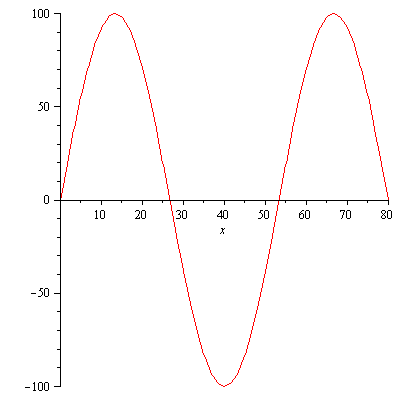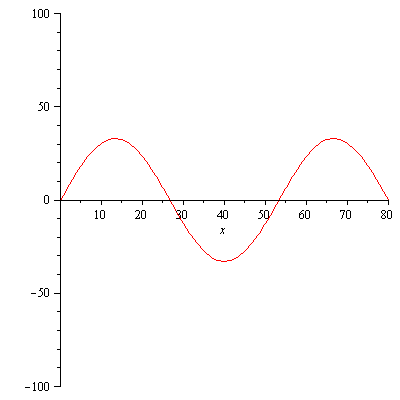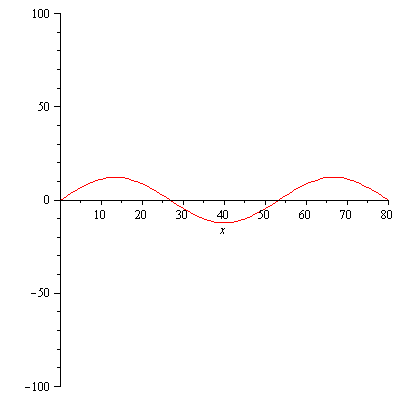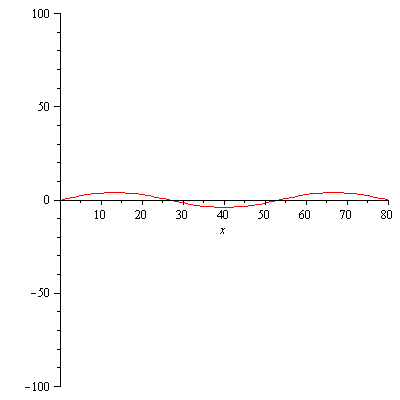
f:=x->100*sin(Pi*x/80); plot(f,0..80); |
| > |
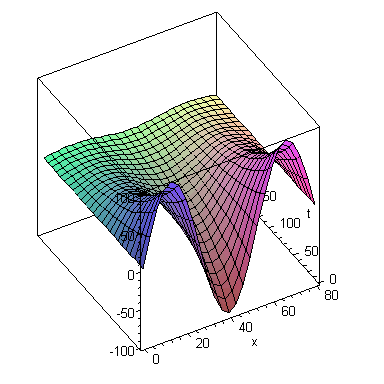
u:=(x,t)->100*sin(Pi*x/80)*exp(-0.001785*t); |
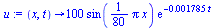 |
(2.1) |
| > |
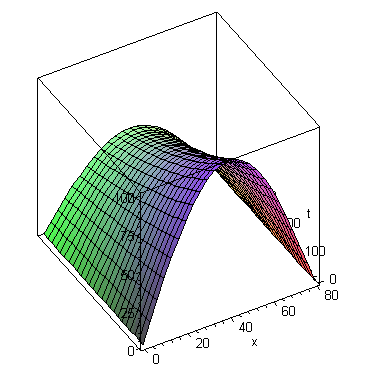
plot3d(u(x,t),x=0..80,t=0..400,axes=box); |
| > |
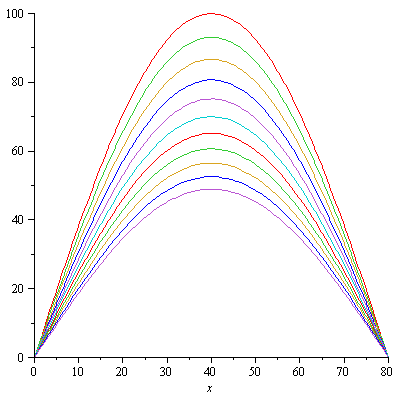
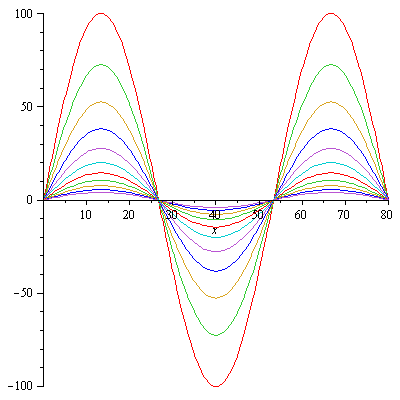
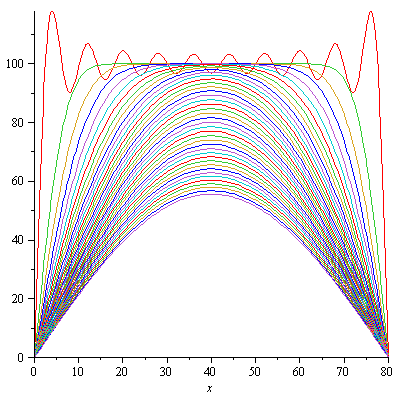
plot([seq(u(x,t),t=[seq(i*40,i=0..10)])],x=0..80); |
| > |
with(plots):animate(u(x,t),x=0..80,t=0..400,frames=30); |
Exa 2. Muuten sama, mutta nyt
| > |
setoptions3d(orientation=[-120,50],axes=box): |
| > |
f:=x->100*sin(3*Pi*x/80); plot(f,0..80); |
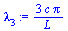 |
(2.2) |
| > |
c:=sqrt(1.158):L:=80: lambda[3]; |
 |
(2.3) |
| > |
u:=(x,t)->100*sin(3*Pi*x/L)*exp(-lambda[3]^2*t); |
![proc (x, t) options operator, arrow; `+`(`*`(100, `*`(sin(`+`(`/`(`*`(3, `*`(Pi, `*`(x))), `*`(L)))), `*`(exp(`+`(`-`(`*`(`^`(lambda[3], 2), `*`(t))))))))) end proc](images/lampoyhtalo_11.gif) |
(2.4) |
| > |
plot3d(u(x,t),x=0..80,t=0..200,axes=box); |
"Aikasiivuparvi" :
| > |
#[seq(u(x,t),t=[seq(i*0.1,i=0..5)])]; |
Tällainen lausekkeiden lista voidaan antaa suoraan plot:lle, kuten tiedämme: Otetaan samantien enemmän aikaviipaleita.
| > |
plot([seq(u(x,t),t=[seq(i*20,i=0..10)])],x=0..80); |
| > |
animate(u(x,t),x=0..80,t=0..200,frames=30); |
Esim. 3
| > |
summaf:=(x,t,N)->400/Pi*add(1/(2*k-1)*sin((2*k-1)*Pi*x/80)*exp(-(lambda(2*k-1))^2*t),k=1..N); |
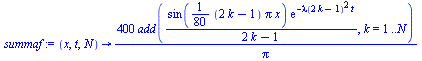 |
(2.5) |
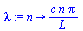 |
(2.6) |
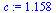 |
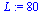 |
(2.7) |
| > |
plot3d(summaf(x,t,10),x=0..L,t=0.1..300,axes=box); |
Summafunktion "aikasiivuparvi" :
| > |
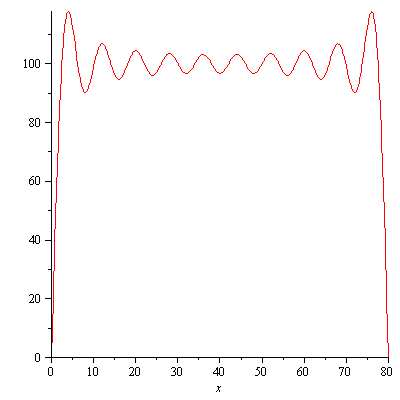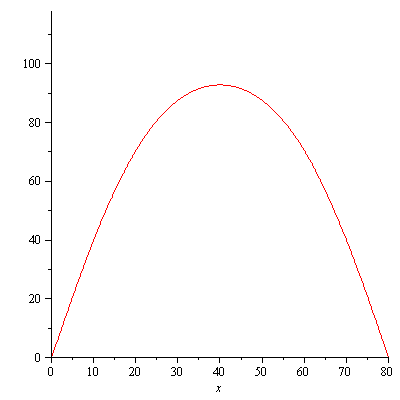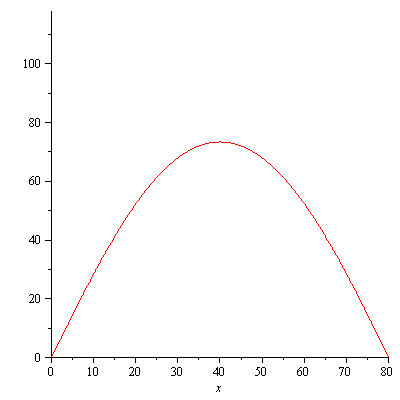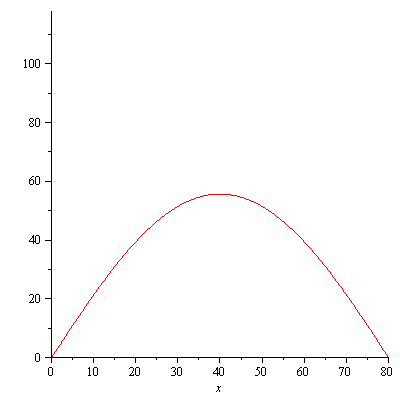
plot([seq(summaf(x,t,10),t=[seq(10*i,i=0..40)])],x=0..L); |
| > |
animate(summaf(x,t,10),x=0..L,t=0..400,frames=60,numpoints=200); |
Muuttujien erottelu
| > |
restart:
with(LinearAlgebra): with(plots): |
| > |
setoptions3d(orientation=[-120,50],axes=box): |
| > |
#read("c:\\usr\\heikki\\numsym05\\maple\\ns05.mpl"); |
| > |
# read("/p/edu/mat-1.192/ns05.mpl"); |
| > |
osdy:=c^2*diff(u(x,t),x$2)=diff(u(x,t),t);eval(subs(u(x,t)=F(x)*G(t), osdy)); |
| > |
separoitu:=simplify(%/(c^2*F(x)*G(t)));
|
| > |
xyht:=lhs(separoitu)=-p^2;
tyht:=rhs(separoitu)=-p^2;
|
| > |
FDY:=lhs(xyht)*F(x)=rhs(xyht)*F(x); |
| > |
GDY:=c^2*lhs(tyht)*G(t)=c^2*rhs(tyht)*G(t); |
| > |
ff:=rhs(dsolve(FDY,F(x)));
dsolve(GDY,G(t)): gg:=rhs(%); |
| > |
ff:=subs(_C2=A,_C1=B,ff); gg:=subs(_C1=1,gg); |
RE1 & RE2 ==>
| > |
ff:=subs(A=0,B=1,p=n*Pi/L,ff);
|
| > |
u:=sum(B[n]*ff*gg,n=1..infinity); |
Sinisarjaksi:
Alkuehto saadaan toteutumaan valitsemalla B[n]:t AE-funktion f (2L-jaksoisen) sinisarjan kertoimiksi.
Määritellään sinisarjan kertoimet ja annetaan alkuarvofunktion f sekä jakson puolikkaan L olla
vapaita, myöhemmin annettavia symboleja (vrt. fourier.mws-työarkki).
| > |
f:='f':L:='L':n:='n':Bn:=(2/L)*Int(f(x)*sin(n*Pi*x/L),x=0..L); |
Otetaan esimerkiksi KRE s. 648, Exa 3
| > |
f:=x->piecewise(x<L/2,x,x>L/2,L-x);L:=Pi; |
 :n pituinen sauva sopiii matemaatikoille.
:n pituinen sauva sopiii matemaatikoille.
| > |
bn:=simplify(value(Bn)); |
| > |
summaf:=(x,t,N)->add(un,n=1..N); |
| > |
plot3d(summaf(x,t,5),x=0..Pi,t=0..2,axes=box); |
Summafunktion "aikasiivuparvi" :
| > |
[seq(summaf(x,t,5),t=[seq(i*0.1,i=0..5)])]; |
Tällainen lausekkeiden lista voidaan antaa suoraan plot:lle, kuten tiedämme: Otetaan samantien enemmän aikaviipaleita.
| > |
plot([seq(summaf(x,t,40),t=[seq(i*0.1,i=0..10)])],x=0..Pi); |
| > |
animate(summaf(x,t,40),x=0..Pi,t=0..10,frames=30); |
Eristetyt päät, adiabaattiset reunaehdot
| > |
restart:
with(plots):setoptions3d(orientation=[-120,50],axes=box): |
| > |
#read("c:\\usr\\heikki\\numsym05\\maple\\ns05.mpl"); |
| > |
#uu:=(x,t,n)->cos(n*Pi*x/L)*exp(-(c*n*Pi/L)^2*t); |
| > |
#usum:=(x,t,N)->add(a(n)*uu(x,t,n),n=0..N); |
| > |
#f:='f':L:='L':n:='n':an:=(2/L)*Int(f(x)*cos(n*Pi*x/L),x=0..L); |
Esimerkiksi KRE s. 64x, Exa 4
| > |
f:=x->piecewise(x<L/2,x,x>L/2,L-x);L:=Pi; |
| > |
a:=n->2/L*int(x*cos(n*Pi*x/L),x=0..L/2)+2/L*int((L-x)*cos(n*Pi*x/L),x=L/2..L); |
| > |
a(0):=1/L*(int(x,x=0..L/2)+int(L-x,x=L/2..L)); |
| > |
u:=(x,t,N)->L/4-8/L/Pi^2*sum(1/(4*k-2)^2*cos((4*k-2)*Pi/L*x)*exp(-(((4*k-2)*c*Pi/L)^2)*t),k=1..N); |
| > |
plot3d(u(x,t,10),x=0..Pi,t=0..2,axes=box); |
Summafunktion "aikasiivuparvi" :
| > |
#[seq(usum(x,t,20),t=[seq(i*0.1,i=0..5)])]; |
Tällainen lausekkeiden lista voidaan antaa suoraan plot:lle, kuten tiedämme: Otetaan samantien enemmän aikaviipaleita.
| > |
plot([seq(u(x,t,10),t=[seq(i*0.1,i=0..10)])],x=0..Pi); |
| > |
animate(u(x,t,20),x=0..Pi,t=0..2,frames=30); |