Tentti 3.2.2007
Ratkaisut / HA
Tämä Maple-työarkki täydentää tiedostoa
helmi07ratkaisut.pdf
Alustukset
| > |
with(LinearAlgebra):alias(Inv=MatrixInverse,Diag=DiagonalMatrix,Det=Determinant,Id=IdentityMatrix,ref=GaussianElimination):
|
| > |
pyorista:=(x,nn)->evalf(round(10^nn*x)/10^nn):
|
Tehtävä 1.
| > |
A:=<<1,-4,-3>|<3,2,-2>|<4,-6,-7>>;
|
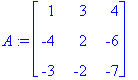
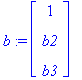
| > |
Ab:=<A | b>; # Liitännäismatriisi
|
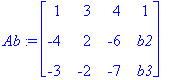
| > |
rAb:=ref(Ab); # Gaussataan ref-muotoon
|
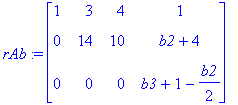
Jotta ratkaisuja on, jos ja vain jos viimeinen sarake ei ole tukisarake, ts.
| > |
ehto:=b3+1-b2/2 = 0; # Kohdan (a) vastaus:
|
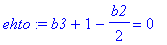
(b)-kohta:
| > |
Ab:=subs(b3=-2,rAb); # Sijoitetaan b3:lle arvo -2 Gaussatussa liitännäismatriisin.
|

| > |
b3:=-2: b2:=solve(ehto,b2); # Tietysti nähdään heti suoraan yllä olevastakin.
|
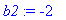
| > |
Ab; # Ab:ssä sioitettu b2:=-2;
|

Takaisinsijoitus:
| > |
14*x2+10*x3 = 2; x2:=solve(%,x2);
|
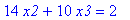
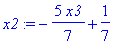
| > |
x1+3*x2+4*x3 = 1; x1:=solve(%,x1);
|
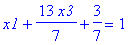
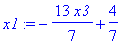
Jos merkitään
x3 = t = vapaa,
saadaan yleinen ratkaisu muotoon
| > |
array([[x[1] = -13*t/7 +1-3/7],[x[2] = -5*t/7 + 1/7], [x[3] = t]]);
|
![matrix([[x[1] = -13/7*t+4/7], [x[2] = -5/7*t+1/7], [x[3] = t]])](images/helmi07ratk13.gif)
Tehtävä 2.
(c)-kohta
| > |
P:=<<.93,.03,.04>|<.02,.93,.05>|<.04,.04,.92>>;
|

Lasketaan ominaisarvoa 1 vastaava ominaisvektori:
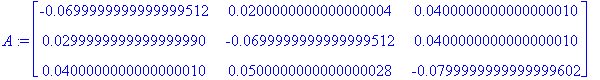
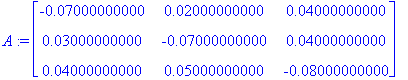
| > |
Ab:=A: # "b"-sarake on 0, joten sitä ei tarvita.
|
Suoritetaan Gauss-askeleet Maplella käsinlaskua matkien:
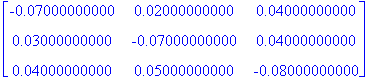
| > |
kerroin:=Ab[2,1]/Ab[1,1]: Ab[2,1..-1]:=Ab[2,1..-1]-kerroin*Ab[1,1..-1]:Ab:=map(pyorista,Ab,3);
|
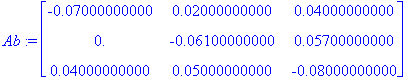
| > |
kerroin:=Ab[3,1]/Ab[1,1]: Ab[3,1..-1]:=Ab[3,1..-1]-kerroin*Ab[1,1..-1]: Ab:=map(pyorista,Ab,3);
|
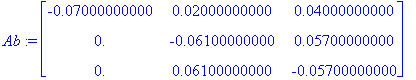
| > |
kerroin:=Ab[3,2]/Ab[2,2]: Ab[3,1..-1]:=Ab[3,1..-1]-kerroin*Ab[2,1..-1]: Ab:=map(pyorista,Ab,3);
|
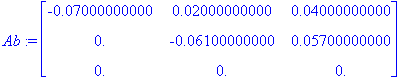
| > |
x2:='x2': -0.061*x2+0.057*x3=0: x2:=solve(%,x2);latex(%,"huu.tex",append);
|
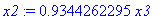
| > |
x1:='x1': -0.07*x1 + 0.02*x2 + 0.04*x3 =0: x1:=solve(%,x1);latex(%,"huu.tex",append);
|
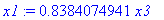
| > |
x3:=10: [x1,x2,x3];summa:=sum(%[i],i=1..3);
|
![[8.384074941, 9.344262295, 10]](images/helmi07ratk23.gif)
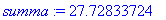
| > |
100*<x1,x2,x3>/summa: map(pyorista,%,2);
|
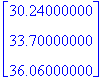
(d)-kohtaan:
| > |
map(Re,Eigenvalues(P));
|
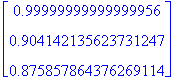
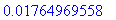
Tehtävä 3.
| > |
with(LinearAlgebra):with(plots):#with(plottools):
|
Warning, the name changecoords has been redefined
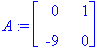
| > |
(lambda,ov):=Eigenvectors(A);
|
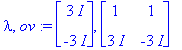
(a)
| > |
lambda:=3*I; w:=<1,3*I>;
|
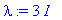
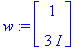
| > |
#A.w = lambda*w; # Tarkistetaan, että on tosiaan ominaisarvo/-vektori
|
| > |
# Kompleksinen muoto, jota ei tässä käytetä:
|
| > |
# Y:=C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2;
|
Mennään suoraan reaalisen muotoon, kaavahan on annettu.
| > |
alpha:=Re(lambda); # Ominaisarvon reaaliosa
|
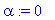
| > |
beta:=Im(lambda); # Ominaisarvon imag-osa
|
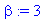
| > |
u:=map(Re,w); v:=map(Im,w); # Omiaisvektorin Re- ja Im-osavektorit
|
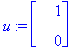
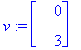
| > |
uv:=<u|v>; # Ladotaan vierekkäin
|
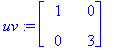
| > |
Kiertomatr:=<<cos(beta*t),-sin(beta*t)>|<sin(beta*t),cos(beta*t)>>;
|
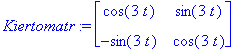
| > |
Y:=exp(alpha*t)*(uv.Kiertomatr.<a,b>);
|
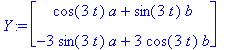
| > |
subs(t=0,Y)=<1,0>; # Alkuarvo y(0)=[1,0]
|
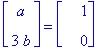
| > |
a:=1; b:=0; Y; # Sijoitetaan ratkaisut a:=1 ja b:=0 ja katsotaan Y.
|
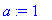
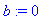
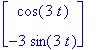
Trajektori on ellipsi, jonka puoliakselit ovat 1 ja 3, kierretään myötäpäivään, kun t kasvaa.
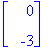
| > |
plot([Y[1],Y[2],t=0..3*Pi/3],scaling=constrained):kuva:=%:
|
| > |
display(kuva,plots[arrow](<1,0>,-0.5*<0,1>,width=1/16));
|
![[Maple Plot]](images/helmi07ratk44.gif)
| > |
Pisteet:=[<0,-3>,<-1,0>,<0,3>,<1,0>];
|
![Pisteet := [Vector(%id = 3032656), Vector(%id = 2989288), Vector(%id = 2989108), Vector(%id = 2988928)]](images/helmi07ratk45.gif)
| > |
suunnat:=map(p->A.p,Pisteet);suunnat;
|
![suunnat := [Vector(%id = 17141288), Vector(%id = 17550860), Vector(%id = 17949792), Vector(%id = 18171944)]](images/helmi07ratk46.gif)
![[Vector(%id = 17141288), Vector(%id = 17550860), Vector(%id = 17949792), Vector(%id = 18171944)]](images/helmi07ratk47.gif)
| > |
suunnat:=map(v->1/5*v,suunnat);
|
![suunnat := [Vector(%id = 2468148), Vector(%id = 17336456), Vector(%id = 16310448), Vector(%id = 2625024)]](images/helmi07ratk48.gif)
| > |
display(kuva,seq(plots[arrow](Pisteet[i],suunnat[i]),i=1..4));
|
![[Maple Plot]](images/helmi07ratk49.gif)
| > |
parvi:=seq(seq([Y[1],Y[2],t=0..2],a=-2..2),b=-2..2):
|
| > |
plot([parvi],scaling=constrained):
|
| > |
display(kuva,DEplot([D(y1)(t)=y2(t),D(y2)(t)=-9*y1(t)],
[y1(t),y2(t)],t=0..2,y1=-3..3,y2=-9..9,color=grey,stepsize=.02),title="",thickness=1,labels=["y1","y2"]);
|
![[Maple Plot]](images/helmi07ratk50.gif)
Tehtävä 4.
| > |
F:=(t,Y)-><Y[2],-3*Y[1]+t*Y[2]>;
|
![F := proc (t, Y) options operator, arrow; `<,>`(Y[2],-3*Y[1]+t*Y[2]) end proc](images/helmi07ratk51.gif)
![Y[0] := Vector(%id = 17666156)](images/helmi07ratk52.gif)
| > |
Y[1]:=Y[0]+h*F(0,Y[0]);
|
![Y[1] := h*Vector(%id = 18334668)+Vector(%id = 17666156)](images/helmi07ratk53.gif)
(a) Yksi Euler-askel: h=0.2.
| > |
Ya:=subs(h=0.2,Y[1]); evalm(%);
|
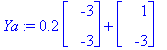
![vector([.4000000000, -3.600000000])](images/helmi07ratk55.gif)
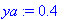
(b) Kaksi Euler-askelta, h=0.1
| > |
Yb[1]:=subs(h=0.1,Y[1]);(evalm(%));
|
![Yb[1] := .1*Vector(%id = 18334668)+Vector(%id = 17666156)](images/helmi07ratk57.gif)
![vector([.7000000000, -3.300000000])](images/helmi07ratk58.gif)
| > |
Yb[2]:=Yb[1]+0.1*F(0.1,Yb[1]);
|
![Yb[2] := Vector(%id = 17939004)](images/helmi07ratk59.gif)
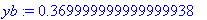
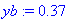
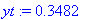
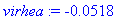
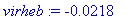
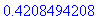
Tehtävä 5
Tehtävä on (aivan tarkoituksella) aivan samanlainen kuin joulukuun 2006 tentissä teht. 5. Pari numeroarvoa vain on muutettu.
Tässä tyydytään suorittamaan lasku Maplella.
Ensin alustus ja latauskomentoja ("ignore").
| > |
with(plots):setoptions3d(orientation=[-30,50],axes=box):
|
| > |
read("c:/usr/heikki/numsym05/maple/ns05.mpl");
|
Tarvitsemme sinisarjaa.
| > |
bn:=(2/L)*int(f(x)*sin(n*Pi*x/L),x=0..L);
|
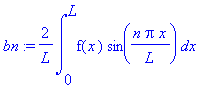
| > |
L:=10: f:=x->50; # Kehitettävä vakiofunktio f=50 välillä [0,10], jakson puolikas L=10.
|
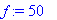
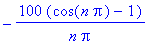
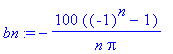
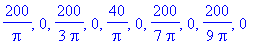
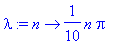
| > |
u:=(x,t,N)->200/Pi*sum(1/(2*k-1)*sin((2*k-1)*Pi*x/10)*exp((-lambda(2*k-1)^2)*t),k=1..N);
|
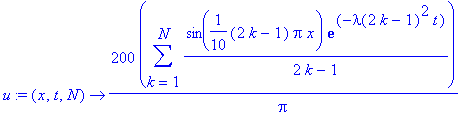
Warning, the name changecoords has been redefined
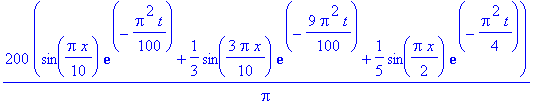
Piirretään pintakuva.
| > |
plot3d(u(x,t,20),x=0..10,t=0..20);
|
![[Maple Plot]](images/helmi07ratk74.gif)
Lisäksi lämpötilaprofiilit 0.5 s välein. Alin on ajanhetkellä t=20, nähdään, että silloin maxlämpötila
menee jo hiukan alle 10 asteen.
| > |
plot([seq(u(x,t,20),t=[seq(j*0.5,j=0..40)])],x=0..10);
|
![[Maple Plot]](images/helmi07ratk75.gif)
Sarjan 1. termi:
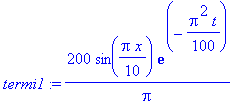
| > |
maxlampotila:=subs(x=5,termi1); # maximi on keskipisteessä.
|
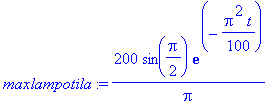
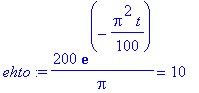
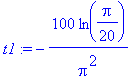
Ihminen kirjoittaisi tuon plus-merkkisenä vaihtaen osoittajan muotoon
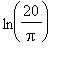 .
.
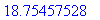
Siinäpä se!
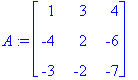
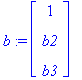
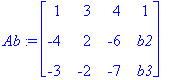
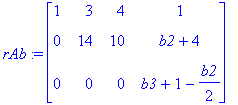
![]()

![]()

![]()
![]()
![]()
![]()
![matrix([[x[1] = -13/7*t+4/7], [x[2] = -5/7*t+1/7], [x[3] = t]])](images/helmi07ratk13.gif)

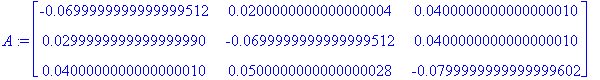
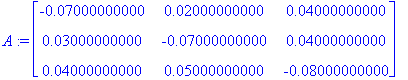
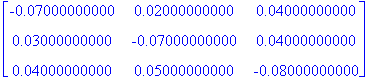
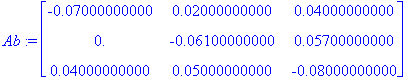
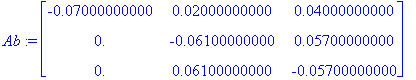
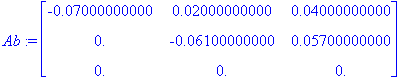
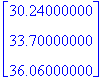
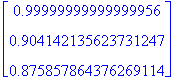
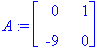
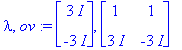
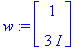
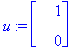
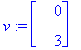
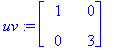
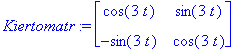
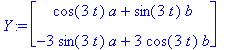
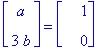
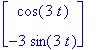
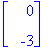
![[Maple Plot]](images/helmi07ratk44.gif)
![Pisteet := [Vector(%id = 3032656), Vector(%id = 2989288), Vector(%id = 2989108), Vector(%id = 2988928)]](images/helmi07ratk45.gif)
![suunnat := [Vector(%id = 17141288), Vector(%id = 17550860), Vector(%id = 17949792), Vector(%id = 18171944)]](images/helmi07ratk46.gif)
![[Vector(%id = 17141288), Vector(%id = 17550860), Vector(%id = 17949792), Vector(%id = 18171944)]](images/helmi07ratk47.gif)
![suunnat := [Vector(%id = 2468148), Vector(%id = 17336456), Vector(%id = 16310448), Vector(%id = 2625024)]](images/helmi07ratk48.gif)
![[Maple Plot]](images/helmi07ratk49.gif)
![[Maple Plot]](images/helmi07ratk50.gif)
![Y[0] := Vector(%id = 17666156)](images/helmi07ratk52.gif)
![Y[1] := h*Vector(%id = 18334668)+Vector(%id = 17666156)](images/helmi07ratk53.gif)
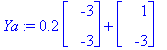
![Yb[1] := .1*Vector(%id = 18334668)+Vector(%id = 17666156)](images/helmi07ratk57.gif)
![Yb[2] := Vector(%id = 17939004)](images/helmi07ratk59.gif)
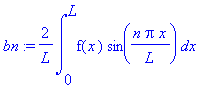
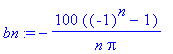
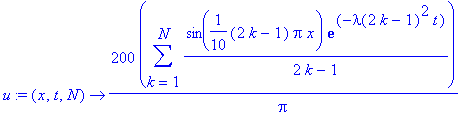
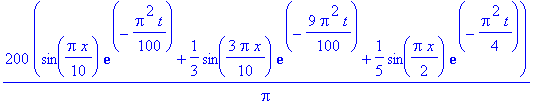
![[Maple Plot]](images/helmi07ratk74.gif)
![[Maple Plot]](images/helmi07ratk75.gif)
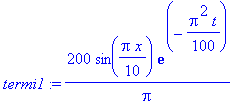
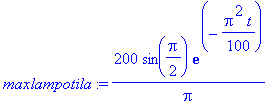
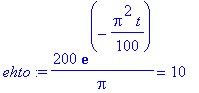
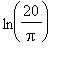 .
.