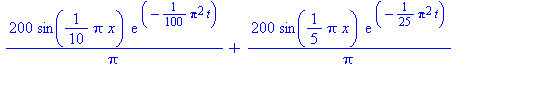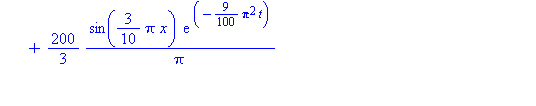Tentti 31.3.2007
Alustukset
| > |
with(LinearAlgebra):with(linalg):alias(Inv=MatrixInverse,Diag=DiagonalMatrix,Det=Determinant,Id=IdentityMatrix,ref=GaussianElimination,rref=ReducedRowEchelonForm): |
Warning, the name GramSchmidt has been rebound
Warning, the protected names norm and trace have been redefined and unprotected
1.
| > |
A:=<<0,1,4>|<1,0,-3>|<2,3,8>>; |
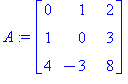
Katsotaan ensin tulos ja periaate valmiista Maple-funktiota käyttäen.
| > |
<A | Id(3)>,rref(<A|Id(3)>); # A:n viereen 3 x 3-yksikkömatriisi ja rref koko höskälle käyttäen Maplen valmista rref-funktiota |
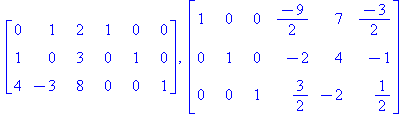
Koska vasemmalle saadaan yksikkömatriisi, ts. kaikki sarakkeet ovat tukisarakkeita, on käänteismatriisi olemassa ja se koostuu yllä olevista
kolmesta viimeisestä rivistä.
Tehdään laskut nyt vaiheittain (Maplella käsinlaskua simuloiden):
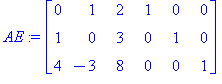
| > |
AE:=Matrix(swaprow(AE,1,2)); # Vaihdetaan 1. ja 2. rivi |
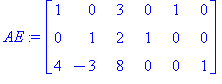
| > |
AE[3,1..-1]:=AE[3,1..-1]-4*AE[1,1..-1]: AE; # rivi3:=-4*rivi1+rivi3 |
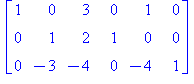
| > |
AE[3,1..-1]:=AE[3,1..-1]+3*AE[2,1..-1]:AE; # rivi3:=3*rivi2+rivi3 |
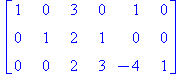
Tästä nähdään, että A:n kaikki sarakkeet ovat tukisarakkeita ja niin ollen käänteismatriisi on olemassa.
| > |
AE[3,1..-1]:=AE[3,1..-1]/2:AE; # Skaalataan alin tukialkio 1:ksi. |
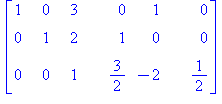
Alhaalta ylös:
| > |
AE[2,1..-1]:=AE[2,1..-1]-2*AE[3,1..-1]:AE; # rivi2:=-3*rivi3+rivi2 |
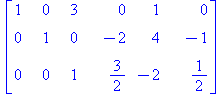
| > |
AE[1,1..-1]:=AE[1,1..-1]-3*AE[3,1..-1]:AE; # rivi1:=-3*rivi3+rivi1 |
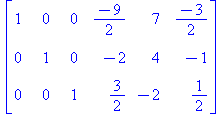
Päästiin siten samaan tulokseen kuin yllä valmiilla rref-funktiolla ja käänteismatriisi on siten
| > |
![AE[1 .. 3, 4 .. 6]; 1](Aimages/Amaalis07_10.gif) |
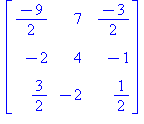
Huomioita: Tässä ei todellakaan tarvitse laskea yhtään determinanttia, johtopäätös tulee suoraan laskenta-algoritmista.
Teoriassa voisi esiintyä ratkaisu, jossa johtopäätös olemassaolosta tehdään determinantista. Kyllä sekin hyväksytään, vaikka
onkin hiukan "huonoa makua" osoittava.
2
| > |
A:=<<5,0,0,0>|<-2,3,0,0>|<6,c,5,0>|<-1,0,4,1>>; |
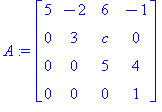
Koska kyseessä on yläkolmiomatriisi, ovat ominaisarvot matriisin diagonaalialkiot. Jos et sattuisi tätä muistamaan, saat sen suoraan kehittämällä
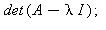 n (alideterminantteineen) ensimmäisen sarakkeen mukaan.
n (alideterminantteineen) ensimmäisen sarakkeen mukaan.
| > |
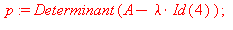 |
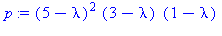
Matriisi (n x n) on diagonalisoituva, jos sillä on n LRT ominaisvektoria, mikä on yhtäpitävää sen kanssa, että kunkin ominaisrvon algebrallinen ja
geometrinen kertaluku yhtyvät. Tässä tapauksessa näin on jos ja vain jos ominaisarvon 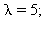 geometrinen kertaluku yhtyy algebralliseen = 2
geometrinen kertaluku yhtyy algebralliseen = 2
Toisin sanoen, laskettava ominaisarvoa 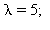 vastaavat ominaisvektorit ja järjestettävä parametrin c avulla tilanne sellaiseksi, että saadaan
vastaavat ominaisvektorit ja järjestettävä parametrin c avulla tilanne sellaiseksi, että saadaan
2 LRT ominaisvektoria.
| > |
(lam,V):=Eigenvectors(A); |
, Matrix(%id = 409917796)](Aimages/Amaalis07_18.gif)
![[1, 1, {table( [( 1 ) = 1/4*c+7/4, ( 2 ) = 1/2*c, ( 3 ) = -1, ( 4 ) = 1 ] )}], [5, 2, {table( [( 1 ) = 1, ( 2 ) = 0, ( 3 ) = 0, ( 4 ) = 0 ] )}], [3, 1, {table( [( 1 ) = 1, ( 2 ) = 1, ( 3 ) = 0, ( 4 ) ...](Aimages/Amaalis07_19.gif)
![[1, 1, {table( [( 1 ) = 1/4*c+7/4, ( 2 ) = 1/2*c, ( 3 ) = -1, ( 4 ) = 1 ] )}], [5, 2, {table( [( 1 ) = 1, ( 2 ) = 0, ( 3 ) = 0, ( 4 ) = 0 ] )}], [3, 1, {table( [( 1 ) = 1, ( 2 ) = 1, ( 3 ) = 0, ( 4 ) ...](Aimages/Amaalis07_20.gif)
Kumpikaan ei ota huomioon mahdollisuutta: c=6, poikkeusarvot on aina ja kaikkialla käsiteltävä erikseen.

| > |
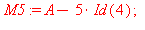 |
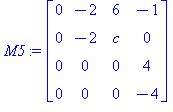
Ominaisvektoriyhtälö on siis 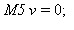 . Merkitään B :llä M5:n kanssa riviekvivalenttia matriisia, joka syntyy rivioperaatioilla.
. Merkitään B :llä M5:n kanssa riviekvivalenttia matriisia, joka syntyy rivioperaatioilla.
(Olkoon B yleisnimi tällaisille.)
| > |
 |
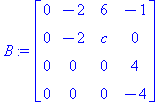
| > |
![B[2, 1 .. -1] := B[2, 1 .. -1]-B[1, 1 .. -1]; -1; B; 1](Aimages/Amaalis07_27.gif) |

Seuraava rivioperaatio riippuu siitä, onko 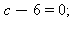 vai ei. Selvyyden vuoksi nollataan ensin alin rivi:
vai ei. Selvyyden vuoksi nollataan ensin alin rivi:
| > |
![B[4, 1 .. -1] := B[4, 1 .. -1]+B[3, 1 .. -1]; -1; B; 1](Aimages/Amaalis07_30.gif) |

Jos c ei ole 6, on systeemin matriisilla 3 tukialkiota (-2,c-6,4) ja siis yksi vapaa parametri, ja siis 1-ulotteinen ominaisavaruus.
Jos c=6, on tukialkioita vain 2 (-2 ja 1), joten vapaita parametreja on 2 ja siten ominaisavaruus on 2-ulotteinen.
Siis matriisi on diagonalisoituva, jos ja vain jos c=6.
Voidaan viedä selvyyden vuoksi loppuun saakka : c=6, lisätään -4*rivi2 kolmanteen riviin:
| > |
![c := 6; -1; B[3, 1 .. -1] := B[3, 1 .. -1]-4*B[2, 1 .. -1]; -1; B; 1](Aimages/Amaalis07_32.gif) |

Tukialkiot sarakkeissa 2 ja 4, vapaat muuttujat sarakkeissa 1 ja 3.
3.
| > |
restart: with(LinearAlgebra): with(linalg): with(plots): |
Warning, the name GramSchmidt has been rebound
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
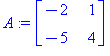
Aloitetaan laskemalla ominaisarvot ja -vektorit. Sitä laskua en enää näytä, kaikkihan sen osaavat!
Antaa Maplen laskea valmiilla funktiolla:
| > |
(lambda,ov):=Eigenvectors(A); |
, Matrix(%id = 411114280)](Aimages/Amaalis07_35.gif)
Siis ominaisarvot ovat -1 ja 3 ja vastaavat ominaisvektorit ovat ov-matriisin sarakkeet:
| > |
v1:=ov[1..-1,1]; v2:=ov[1..-1,2]; |
](Aimages/Amaalis07_36.gif)
](Aimages/Amaalis07_37.gif)
Yleinen ratkaisu:
| > |
y:=t->C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2; |
![proc (t) options operator, arrow; C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2 end proc](Aimages/Amaalis07_38.gif)
| > |
 |
](Aimages/Amaalis07_40.gif)
Alkuarvotehtävä:
 = Vector[column](%id = 408940416)](Aimages/Amaalis07_41.gif)
| > |
LinearSolve(ov,<1,3>); # Ratkaistaan vakiot C1 ja C2: |
](Aimages/Amaalis07_42.gif)
| > |
ya:=unapply(subs(C1=1/2,C2=5/2,y(t)),t): # Maple-tekniikkaa, ei tarvitse lukea. |
| > |
ya(t); # Alkuarvotehtävän ratkaisu koordinaattimuodossa: |
](Aimages/Amaalis07_43.gif)
| > |
plot([Ya[1],Ya[2],t=-2..2],view=[0..5,0..5]); |
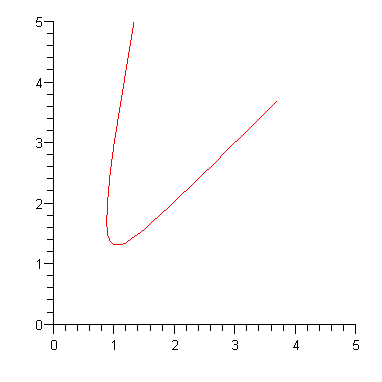
| > |
Ys:=map(eval,subs(t=log(s),y(t))); |
](Aimages/Amaalis07_45.gif)
![table( [( 1 ) = C1/s+1/5*C2*s^3, ( 2 ) = C1/s+C2*s^3 ] )](Aimages/Amaalis07_46.gif)
| > |
#YYa:=subs(C1=1/2,C2=1/2,op(YY)); |
| > |
parvi:=seq(seq([YY[1],YY[2],s=0..4],C2=-2..2),C1=-2..2): |
| > |
parvikuva:=plot([parvi]): |
| > |
display(parvikuva,AAratkuva,plot([[1,3]],style=point,symbol=circle,symbolsize=17),arrow([v1,v2]),view=[-5..5,-5..5]); |
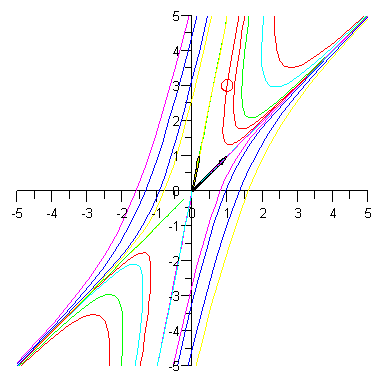
Warning, the previous bindings of the names RationalCanonicalForm and adjoint have been removed and they now have an assigned value
| > |
DEplot([D(y1)(t)=-2*y1(t)+y2(t),D(y2)(t)=-5*y1(t)+4*y2(t)],
[y1(t),y2(t)],t=-5..2,y1=-5..5,y2=-5..5,color=grey): |
| > |
display(kuva,%,title="Satula"); |
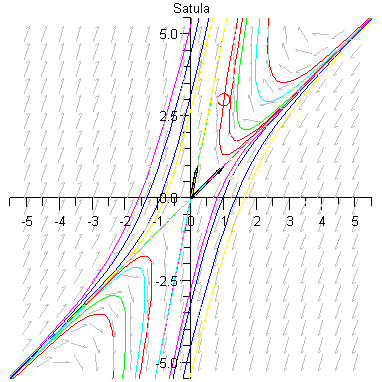
| > |
 |
Selityksiä:
Yleinen ratkaisu:
![y(t) = C1*exp(lambda[1]*t)*v1+C2*exp(lambda[2]*t)*v2; 1](Aimages/Amaalis07_50.gif) missä
missä
, v2 = Vector[column](%id = 410008560)](Aimages/Amaalis07_51.gif)
| > |
!['lambda[1]' = lambda[1], 'lambda[2]' = lambda[2]; 1](Aimages/Amaalis07_52.gif) |
![lambda[1] = -1, lambda[2] = 3](Aimages/Amaalis07_53.gif)
Ominaisvektorilla ![v[1]; 1](Aimages/Amaalis07_54.gif) (C2=0) kuljetaan O:a kohti (
(C2=0) kuljetaan O:a kohti (![lambda[1] < 0; 1](Aimages/Amaalis07_55.gif) ) ja ominaisvektorilla v[2] (C1=0) O:sta poispäin (
) ja ominaisvektorilla v[2] (C1=0) O:sta poispäin (![0 < lambda[2]; 1](Aimages/Amaalis07_56.gif) ).
).
Kyseessä on satulapiste, joka on epästabiili (jo pelkästään ominaisvektorikäytös kertoo sen).
Suuntakenttänuolet annetuissa pisteissä lasketaan yksinkertaisesti näin:
| > |
p1:=<1,0>; s1:=A.p1: s1:=s1/10;#arrow([p1],[s1/10]); |
](Aimages/Amaalis07_57.gif)
](Aimages/Amaalis07_58.gif)
| > |
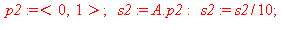 |
](Aimages/Amaalis07_60.gif)
](Aimages/Amaalis07_61.gif)
| > |
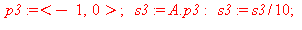 |
](Aimages/Amaalis07_63.gif)
](Aimages/Amaalis07_64.gif)
| > |
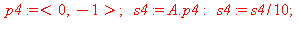 |
](Aimages/Amaalis07_66.gif)
](Aimages/Amaalis07_67.gif)
| > |
; 1](Aimages/Amaalis07_68.gif)
; 1](Aimages/Amaalis07_69.gif) |
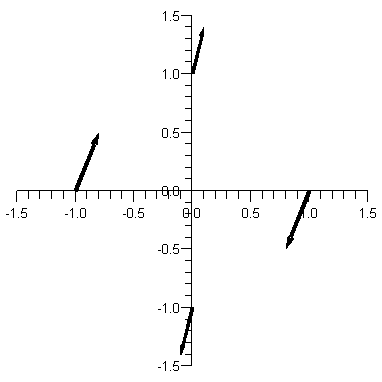
Piirrettiin kuhunkin annettuun pisteeseen p derivaatan suuntainen nuoli s, joka saadaan kertomalla 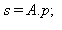 , kun kerran y'=A p. Normeerataan tässä jakamalla 10:llä.
, kun kerran y'=A p. Normeerataan tässä jakamalla 10:llä.
4.
Kriittiset pisteet: Ratkaistaan yhtälöryhmä: "oikeat puolet = 0", ts.
| > |
yhtaloryhma:={200*x-4*x*y=0,-150*y+2*x*y=0}; |
| > |
solve(yhtaloryhma,{x,y}); |
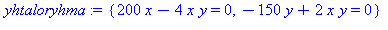
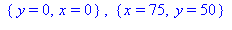
Käsin laskien: 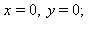 nähdään välittömästi ratkaisuksi (sukupuuttoratkaisu). Jos x ei ole 0, saadaan 1. yhtälöstä:
nähdään välittömästi ratkaisuksi (sukupuuttoratkaisu). Jos x ei ole 0, saadaan 1. yhtälöstä: 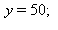 ja sitten toisesta
ja sitten toisesta 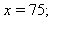 .
.
Muita mahdollisuuksia ei ole.
| > |
krp:=<75,50>; # Hengissä säilymisen kriittinen piste |
](Aimages/Amaalis07_77.gif)
Linearisointi:
| > |
f:=200*x-4*x*y;g:=-150*y+2*x*y; |
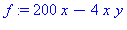
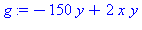
| > |
J:=Matrix(jacobian([f,g],[x,y])); # Jacobin matriisi |
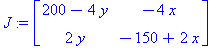
| > |
A:=subs(x=75,y=50,J); # Sijoitetaan kriittinen piste |
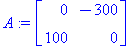
](Aimages/Amaalis07_82.gif)
Puhtaasti imaginaariset ominaisarvot, KRP:n tyyppi on siten keskus ja siis stabiili.
Huom: Keskuksen tapauksessa linearisoidun systeemin (O:n) tyyppi ei välttämättä kerro alkuperäisen systeemin (KRP:n) tyyppiä.
Tässä tapauksessa se on sama, mutta sitä ei tehtävässä pyydetty pohtimaan (keinoja siihen ei kurssilla ole edes opetettu).
5.
Tehtävä on periaatteessa samanlainen kuin kahdessa edellisessä tentissä. Nyt on alkuarvofunktio määritelty paloittain kahdessa osassa.
Se on tehty edelleenkin mahdollisimman humaanisti integrointivaivoja säästäen.
Älä välitä ylimääräisistä Maple-komennoista. (Vaikka ovat punaisella, niin älä sinä ala nähdä punaista!)
| > |
 |
| > |
with(plots):setoptions3d(orientation=[-30,50],axes=box): |
Warning, the name changecoords has been redefined
| > |
read("c:/usr/heikki/numsym05/maple/ns05.mpl"); |
Ratkaisun muoto on annettu.
Jotta alkuehto toteutuisi, on ![B[n]; 1](Aimages/Amaalis07_84.gif) - kertoimet valittava alkuehtofunktion f sinisarjan kertoimiksi:
- kertoimet valittava alkuehtofunktion f sinisarjan kertoimiksi: ![B[n] = b[n]; 1](Aimages/Amaalis07_85.gif) .
.
Tarvitsemme siis sinisarjaa.
| > |
bn:=(2/L)*int(f(x)*sin(n*Pi*x/L),x=0..L); |
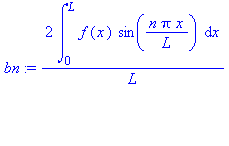
| > |
bn := (2/10)*(Int(100*sin(n*Pi*x/10),x=0..5)+Int(O*sin(n*Pi*x/10),x=5..10)); |
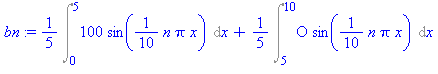
| > |
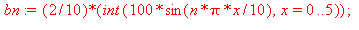 |
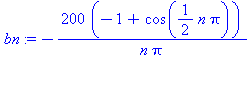
| > |
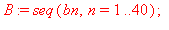 |
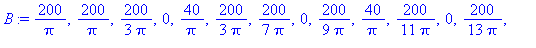
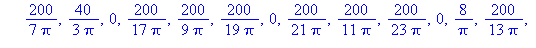
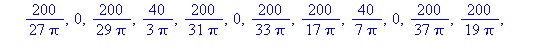

| > |
seq(-1+cos((n*Pi)/2),n=1..10); |
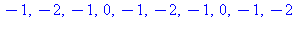
Kertoimet ovat siis muotoa:
| > |
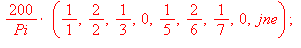 |
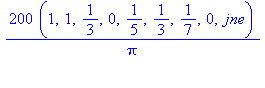
Muodostetaan yleinen n:s osasumma:
| > |
lambda:=n-> n*Pi/10; summaf:=(x,t,N)-> sum(B[n]*sin((n*Pi*x)/10)*exp(-lambda(n)^2*t),n=1..N); |
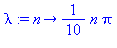
![proc (x, t, N) options operator, arrow; sum(B[n]*sin(1/10*n*Pi*x)*exp(-lambda(n)^2*t), n = 1 .. N) end proc](Aimages/Amaalis07_99.gif)
Kysytty 3:n termin summa on siis:
| > |
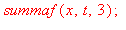 |
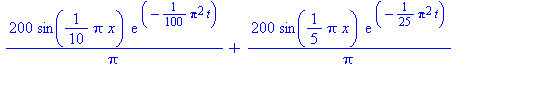
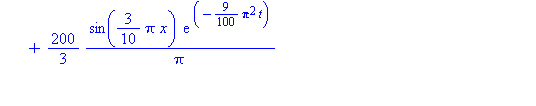
| > |
plot3d(summaf(x,t,3),x=0..10,t=0..20,title="n=3");plot3d(summaf(x,t,20),x=0..10,t=0..20,title="n=20");plot3d(summaf(x,t,40),x=0..10,t=0..20,title="n=40"); |
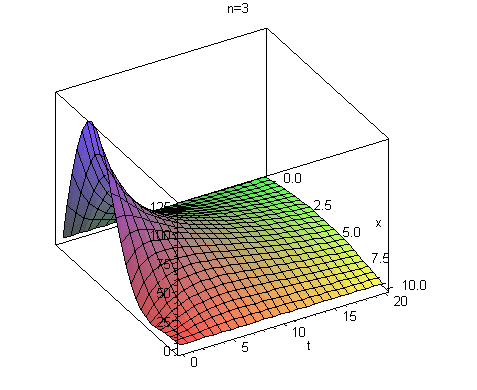
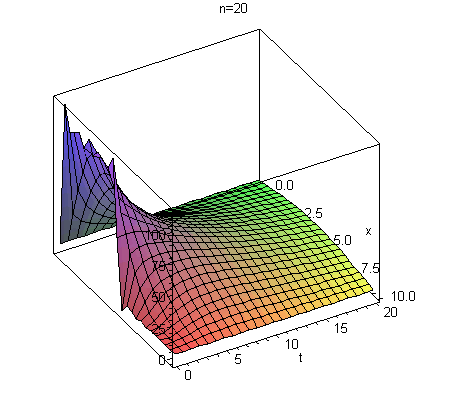
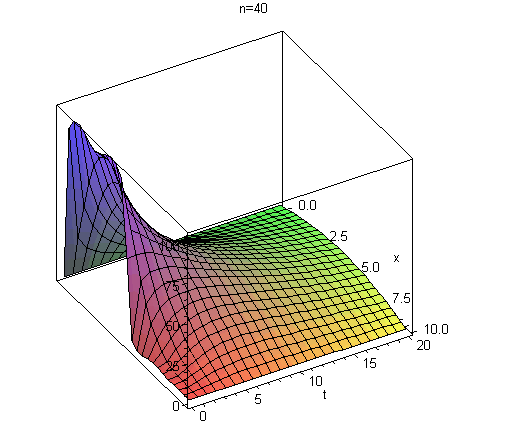
Huomataan, että n=3 on varsin karkea alkuapproksimaatio, n=20 näyttää Gibbsin ilmiön hyvin selvästi. Toki Gibbsin ilmiö esiintyy isommillakin,
mutta kokonaisuus näkyy sileämpänä isommalla n:n arvolla. (Gibbs-piikit ovat hyvin lähellä epäjatkuvuuskohtia, eikä 3D-grafiikka välttmättä näytä
niitä.) Kun aikaa kuluu, niin ratkaisu siliää varsin nopeasti, johtuen exp-termeistä.
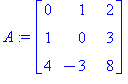

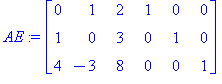
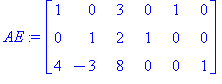
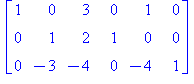
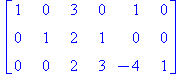
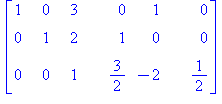
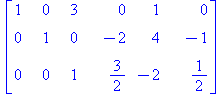
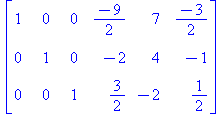
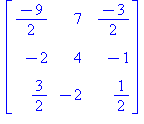
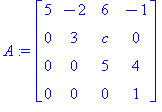
, Matrix(%id = 409917796)](Aimages/Amaalis07_18.gif)

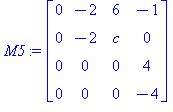
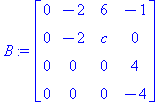



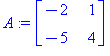
, Matrix(%id = 411114280)](Aimages/Amaalis07_35.gif)
](Aimages/Amaalis07_36.gif)
](Aimages/Amaalis07_37.gif)
](Aimages/Amaalis07_40.gif)
 = Vector[column](%id = 408940416)](Aimages/Amaalis07_41.gif)
](Aimages/Amaalis07_43.gif)

](Aimages/Amaalis07_45.gif)


, v2 = Vector[column](%id = 410008560)](Aimages/Amaalis07_51.gif)
](Aimages/Amaalis07_57.gif)
](Aimages/Amaalis07_58.gif)
](Aimages/Amaalis07_60.gif)
](Aimages/Amaalis07_61.gif)
](Aimages/Amaalis07_63.gif)
](Aimages/Amaalis07_64.gif)
](Aimages/Amaalis07_66.gif)
](Aimages/Amaalis07_67.gif)
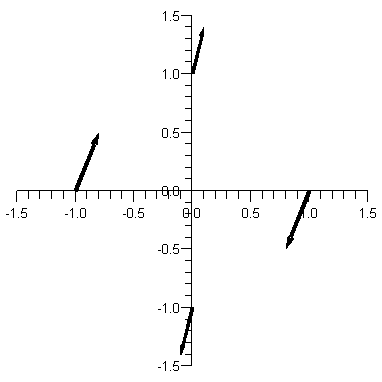
](Aimages/Amaalis07_77.gif)
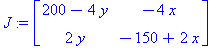
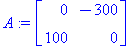
](Aimages/Amaalis07_82.gif)
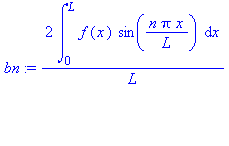
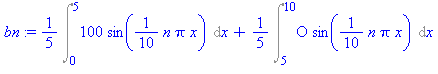
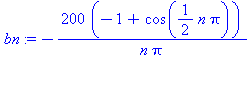
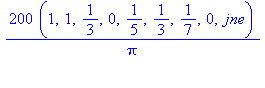
![proc (x, t, N) options operator, arrow; sum(B[n]*sin(1/10*n*Pi*x)*exp(-lambda(n)^2*t), n = 1 .. N) end proc](Aimages/Amaalis07_99.gif)