![[kompl1.gif]](img/kompl1.gif)
Kuvat ovat väreineen havainnollisempia kuin luentoprujussa.
Kirjallisuutta:
Vaativammat tehtävät, joissa tarvitaan analyyttisten ja harmonisten funktioiden ominaisuuksia. Monet virtausdynamiikan, lämpöopin ja sähköstatiikan tehtävät kuuluvat sovellutusten piirin.
Vaikka alkuperäinen tehtävä olisikin reaalialueella muotoiltu, voidaan ratkaisussa joutua kompleksialueelle (esim. ominaisarvotehtävät).
Monet käsitteet saadaan esitetyksi yhtenäisemmässä ja helpommassa muodossa (esim. Fourier-sarjat ja -muunnokset) ja moni puhtaasti reaalifunktioihin liittyvä ilmiö voidaan oikeasti "ymmärtää" vasta kompleksialueella tarkasteltuna.
[KRE8] 12.1, 12.2 (osittain) [Lop] 35.1 [AG]Tarve reaalilukuja laajempaan lukujoukkoon syntyi tarpeesta ratkaista polynomiyhtälöitä. Yksinkertaisin tällainen yhtälö lienee:
x2=-1
Kompleksilukujen nimi ja systemaattisen käyttöönotto on peräisin Gauss:lta. Noudatamme mm. kirjoissa [KRE] ja [AG] esiintyvää tyyliä.
Määritelmä.Kompleksilukuz=(x,y) on
reaalilukupari.Kompleksilukujoukko on reaalilukuparien joukko R2 varustettuna seuraavilla laskutoimituksilla:
|
Huom: Joukkona C on sama kuin R2. Merkintä C viittaa siihen, että käytössä on myös yllä määritelty kertolasku.
Kompleksiluvun z=(x,y) x-koordinaattia sanotaan reaalioasaksi
ja y-koordinaattia imaginaariosaksi, ja merkitään:
x = Re z, y = Im z
Kompleksilukujen kertolasku voidaan muistaa näin:
Tulon reaaliosa = ReRe - ImImMerkitään erityisesti symbolilla i kompleksilukua (0,1) . Edellä oleva esitys voidaan siten kirjoittaa muotoon:
Tulon imaginaariosa = ReIm + ImRe
z=x+yi .
Tässä, kuten aina jatkossa, samastamme: (1,0) = 1, ja yleisesti (x,0)=x.
Nyt saamme kaipaamamme säännön:
i^2 = (0,1)(0,1)=(ReRe-ImIm,ReIm+ImRe)=(-1,0)=-1
Kaikki mystiikka salaperäisen "imaginaarisen" i:n ympäriltä on näin hälvennyt!
Johtopäätös: Kompleksiluvut eivät ole hiukkaakaan "vähemmän reaalisia" kuin reaaliluvut.
Koska opettelemme samalla Matlabia, annamme kuvien tuottamiseen käytetyn
Matlab-koodin. Sen voi www-sivulta suoraan leikata/liimata
Matlab-istuntoon ja tarpeen mukaan modifioida.
clf
z=1+1.5*i
zv=1-1.5*i % Liittoluku (z-viiva)
plot([0 z])
hold on
plot(z,'o')
plot([0 zv],'r')
plot(zv,'o')
axis([-2 2 -2 2])
xlabel('Re-akseli')
ylabel('Im-akseli')
grid
shg
angle(z) % Arg z
ans =
0.9828
![[kompl1.gif]](img/kompl1.gif)
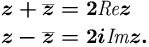
» format compact » z1=8+3*i;z2=9-2*i; » z1-z2 ans = -1.0000 + 5.0000i » z1*z2 ans = 78.0000 +11.0000i » z1/z2 ans = 0.7765 + 0.5059i » format long;z1/z2 ans = 0.77647058823529 + 0.50588235294118i
clf format compact clear n=5; z=1+2*i; plot([0, z]) hold on plot(z,'ob') axis square axis([-2 2 -2 2]) text(real(z),imag(z+0.1*z),num2str(z)) r=sqrt(5) R=r^(1/n) Theta=angle(z) phi=Theta/n+(0:n-1).*(2*pi/n) w=R*(cos(phi)+i*sin(phi)) plot(w,'or') %plot(w,'r') t=linspace(-pi,pi); plot(R*exp(i*t)) for j=0:n-1 text(real(w(j+1)),imag(w(j+1)+0.1*z),['w_',num2str(j)]) end grid shg
![[juuriesim.gif]](img/juuriesim.gif)
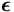 R.
Helpoimmalla pääsemme tällä määritelmällä:
R.
Helpoimmalla pääsemme tällä määritelmällä:
Määritelmä Olkoon z=x+i y, asetetaan
ez = ex (cos y + i sin y).Tässä siis ex tarkoittaa entuudestaan tunnettua reaalista eksponenttifunktiota.
Huom! Exp-funktio voitaisiin määritellä samalla potenssisarjalla, joka pätee reaalialueella. Tällöin ei tarvitsisi tietää mitään reaalisen exp-funktion ominaisuuksista.
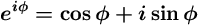
|
%complex/demoexp.m
% 7.5.03
addpath c:\usr\heikki\opemate\complex
x=[-1 0 1]; % Näihin kohtiin 3 pystyviivaa z-tasoon.
y=linspace(-pi/6,3*pi/4,20); % Näihin 20 vaakaviivaa.
m=length(y); n=length(x);
[X,Y]=meshgrid(x,y); % Pysty- ja vaakaviivojen leikkauspisteiden
Z=X+i*Y; % muodostama hila z-tasossa
W=exp(Z); % Hilapisteiden kuvat w-tasossa (exp-funktion arvot)
W=W+i*eps; % Piirtämistä varten lisätään pienenpieni imag-osa siltä
% varalta, että jokin arvo olisi reaalinen.
tol=0.2
ztaso=[min(x)-tol,max(x)+tol,min(y)-tol,max(y)+tol];
%%%%%%%%%%%%%%%%%
figure(1)
clf
axis(ztaso)
hold on
Z=Z+i*eps; % Tällä niksillä varmistetaan, että alkioissa myös imag. osa.
% plot ei nimittäin toimi samalla tavoin reaalisille alkioille.
% (vrt. edellä)
plot(Z(:,1),'b') % 1. pystyviiva sinisellä 'b'
plot(Z(:,2),'g') % 2. vihreällä 'g'
plot(Z(:,3),'c') % 3. värillä 'cyan'
for k=1:m
plot(Z(k,:),'r') % Kaikki 20 vaakaviivaa piirretään punaisella 'r'.
end
title('z-taso')
shg
![[demoexp0.gif]](img/demoexp0.gif)
%%%%%%%%%%%%%%%%%%%%%
figure(2) % Avataan uusi ikkuna w-tasoa varten.
clf
axis square
hold on
plot(W(:,1),'b') % 1. pystyviivan kuva (sininen)
plot(W(:,2),'g') % 2. pystyviivan kuva (vihreä)
plot(W(:,3),'c') % 3. pystyviivan kuva ('cyan')
% Siis kukin w-kuvakäyrä samalla värillä kuin vastaava z-lähtöviiva.
for k=1:m
plot(W(k,:),'r') % Kaikkien 20:n vaakaviivan kuvat punaisella.
end
title('w-taso')
shg
![[demoexp1.gif]](img/demoexp1.gif)
| Pysty- ja vaakaviivojen kuvautuminen exp-funktiossa |
|---|
|
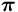 -jaksoisia, ei eksponenttifunktion arvo muutu, jos
y korvataan y+2n
-jaksoisia, ei eksponenttifunktion arvo muutu, jos
y korvataan y+2n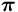 :llä, missä n
:llä, missä n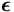 Z (=kokonaisluvut).
Siten exp-funktio on 2
Z (=kokonaisluvut).
Siten exp-funktio on 2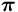 i-jaksoinen, eli eksponenttifunktiolla on puhtaasti
imaginaariset jaksot.
(Tämänhän näemme kuvistakin oikein havainnollisesti.)
i-jaksoinen, eli eksponenttifunktiolla on puhtaasti
imaginaariset jaksot.
(Tämänhän näemme kuvistakin oikein havainnollisesti.)
Siten ez saa kaikki mahdolliset arvonsa 2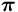 :n korkuisessa
"vyössä", missä x saa kaikki reaaliarvot, eli:
:n korkuisessa
"vyössä", missä x saa kaikki reaaliarvot, eli:
![[jaksovyo]](img/jaksovyo.gif)
clf v=([-20+i*pi, 20+i*pi,20-i*pi, -20-i*pi]) fill(real(v),imag(v),'y') grid
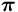 :n korkuisen vyön:
:n korkuisen vyön:
V={z=x+iy | x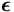 R, y
R, y 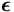 (-
(-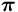 ,
,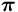 ]}
]}
bijektiivisesti kompleksitasolle, josta on origo poistettu. (Puhumme O:ssa punkteeratusta
tasosta).
Niinpä sillä on käänteiskuvaus, jonka määrittelyjoukko on W0 =
C2 \ {0}.
Saamme siten kuvauksen
Log: W0 ---> V.
Esim (KRE8 Exa 1 s. 681)
Haluamme määrätä kompleksiluvun 3+4i logaritmin.
ez = 3 + 4i .
Olkoon z=x+iy, tällöin
exeiy = 3+4i = 5eiφ, missä;
φ=arg(3+4i) = arctan 4/3 (päähaara).
Siis on oltava
ex = 5
y=φ + 2n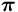
Jos käänteisfunktion arvo valitaan jaksovyöstä V, on y=φ, joten
Log(3+4i) = ln 5 + i arctan 4/3.
Jos merkitsemme log(3+4i):llä mitä tahansa yhtälön ratkaisua, saamme:
log(3+4i) = ln 5 + i(arctan 4/3 + 2n) .
| Saimme laskusäännön logaritmeille: |
|---|
|
w=3+4*i
modw=sqrt(3^2+4^2)
abs(w) % Tarkistetaan, että Matlabin abs toimii kompleksiluvuilla, tottakai!
phii=atan(4/3)
angle(w) % Argumentin päähaara on ohjelmoitu Matlabiin.
% Yksiargumenttinen atan antaa tässä tapauksessa
% myös oikean tuloksen, kuten päättelimme. Yleisesti ei, vaan
% siihen voidaan joutua lisäämään + tai - 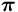 log(5)
log(5)
Tässä yllä olevien komentojen tulokset:
w =
3.0000 + 4.0000i
modw =
5
ans =
5
phii =
0.9273
ans =
0.9273
ans =
0.9273
»
Lasketaan suoraan soveltamalla Matlab:n log-funktiota komplekslukuun:
» log(w)
ans =
1.6094 + 0.9273i
» log(5)
ans =
1.6094
Siis kaikki toimii, kuten pitää. Näemme, että Matlab:n log-funktio laskee
kompleksisen logaritmin päähaaran, kuten luonnollista on.
Huomautus päähaarasta. Käyttämämme (argumentin ja logaritmin)
päähaara (-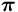 ,
,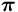 ] on
varsin yleisesti käytetty, mutta tämä on sopimuskysymys. Joissakin
oppikirjoissa käytetään päähaarana väliä (0,2
] on
varsin yleisesti käytetty, mutta tämä on sopimuskysymys. Joissakin
oppikirjoissa käytetään päähaarana väliä (0,2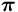 ] (tai [0,2
] (tai [0,2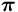 )).
)).
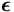 C\{0}.
Kyseessä on siis yhtälön
C\{0}.
Kyseessä on siis yhtälön
ew = z
ratkaiseminen w:n suhteen, kun z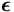 C\{0} on annettu.
C\{0} on annettu.
Olkoon z= r eiφ, ja merkitään w=u+iv. Tällöin siis:
eueiv = r eiφ.Aivan kuten äsken, näemme, että:
u = ln r, v= φ = Arg z.Muut logaritmin haarat saadaan lisäämällä imaginaariosaan v 2
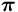 :n monikertoja.
Matlab-ajo: demolog.m
:n monikertoja.
Matlab-ajo: demolog.m
% addpath /home/apiola/opetus/materiaali03/complex
% Laskentaa kompleksisilla logaritmeilla.
% Matlabin funktio log on logaritmin päähaara, siis luentomerkinnöissä
% (ja KRE:ssä) LN.
% Syötteet:
log(-1)
log(i)
log(3+4*i)
moduuli=log(5)
argumentti=angle(3+4*i)
atan(4/3)
atan2(4,3)
log(2)
% Syötteet ja tuosteet:
>> log(-1)
ans =
0 + 3.1416i % pi*i
>> log(i)
ans =
0 + 1.5708i % i*pi/2
>> log(3+4*i)
ans =
1.6094 + 0.9273i
>> moduuli=log(5)
moduuli =
1.6094
>> argumentti=angle(3+4*i)
argumentti =
0.9273
>> atan(4/3)
ans =
0.9273
>> atan2(4,3)
ans =
0.9273
>> log(2) % Posit. reaaliluvun log ja kompleksisen logaritmin
ans = % päähaara ovat samat, koska posit. reaaliluvun
0.6931 % arg = 0