on vektoriavaruus, kun polynomien yhteenlasku ja skalaarilla kertominen määritellään normaaliin tapaan. Samoin korkeintaan astetta n olevien polynomien joukko P_n on vektoriavaruus.

Edelleen kaikkien polynomien joukko P on myös vektoriavaruus.

Vektoriavaruusominaisuuksien toteaminen on silkkaa rutiinia.

Esim3, (jatkuvat) funktiot

   (f+g)(x)=f(x)+g(x)
   (c f)(x)=c(f(x))

Vektoriavaruuden aksioomat on jälleen helppo tarkistaa. (Nolla-vektorina on nollafunktio.)

Monen monia muitakin funktioavaruuksia esiintyy sovellutuksissa.

Esim4, lukujonot

Tuttuja käsitteitä uusissa puitteissa

Vektorialiavaruus

     u  W ja v  W        ==> u+v  W
     u  W , r  R (tai C) ==> ru  W 

Aliavaruudessa pätevät kaikki ominaisuudet ((v1) - (v8)) tietysti. Ts. aliavaruus on osajoukko, joka on itse vektoriavaruus, kun käytetään niitä laskutoimituksia, jotka perusavaruudelta V periytyvät.

Itse asiassa tämä on KRE-kirjan määritelmä Selvitä itsellesi, että 0-vektori on aliavaruudessa ja kunkin vektorin vastavektori! (Huomaa, että edellisessä tarvitaan oletusta "epätyhjä". )

Geometrinen havainnollistus

Muistathan aina tuon tuostakin miettiä, mitä jokin käsite tarkoittaa havainnollisessa geometrisessa maailmassamme. Ajatusviiva ---------

2-d-tasossa aliavaruuksia ovat O:n kautta kulkevat suorat (ja koko avaruus) (ja triviaalilla tavalla pelkkä O).
3-d-avaruudessa aliavaruuksia ovat koko avaruuden ja pelkän O:n lisäksi

• O:n kautta kulkevat suorat
• O:n kautta kulkevat tasot

Mallina vaikkapa taso avaruudessa. Kaksi "tasossa makaavaa", keskenään erisuuntaista vektoria u ja v virittää tason, ts. kaikki tason vektorit voidaan esittää lineaarikombinaatioina: c₁u+c₂v. Taso on 3-ulotteisen avaruuden aliavaruus, jonka virttävät nuo kaksi vektoria. Alla esitettävin merkinnöin: Taso=sp{u,v}

Yleisesti

Olkoot u₁,...u_m 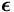V .
Kaikkien lineaarikombinaatioiden joukkoa merk.

sp({u₁,...,u_m}) . Se koostuu muotoa

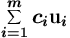
Viritelmä on V:n aliavaruus, koska

• Kahden lineaarikombinaation summa on lineaarikombinaatio
• skaari kertaa lineaarikombinaatio = lineaarikombinaatio

Sanonta: Vektorit u₁,...,u_m virittävät (ali)avaruuden V, jos V=sp({u₁,...,u_m}).

Esim 1, geometriset vektorit

• Yksi nollasta erillinen vektori tasossa tai avaruudessa virittää O:n kautta kulkevan suoran.
• Kaksi erisuuntaista vektoria virittää tason.
• Kolme vektoria, jotka eivät ole saman tason suuntaisia, virittää tavallisen 3-ulotteisen avaruuden.

Esim. 2, Funktioavaruudet

• Polynomiavaruuden P₂ virittävät monomit 1,x,x².
• Monomit 1 ja x² virittävät P₂:n aliavaruuden, joka koostuu korkeintaan astetta 2 olevista polynomeista, joista 1. asteen termi puuttuu.
• Virittääkö kaikkien välillä [a,b] määriteltyjen polynomien avaruus P[a,b] jatkuvien funktioiden avaruuden C[a,b]? No ei varmasti! Osaatko keksiä perustelun?

Lineaarinen riippuvuus/mattomuus LRV/LRT

[KRE8] s. 332 , (Rⁿ:ssä)
[Lay] a. 237 Linearly independent sets, bases

Aiemmin olemme kohdanneet nämä käsitteet Rⁿ:n vektorien yhteydessä. Nyt määrittelemme ne yleisen vektoriavaruuden (abstrakteille) vektoreille. Määritelmät ovat muodollisesti täsmälleen samoja.

Tarkastellaan vektoriyhtälöä

      c1u1 + c2u2 + ... + cmum = 0 

Kaksi mahdollisuutta:

u₁,u₂,...,u_m ovat lineaarisesti riippumattomia (LRT)
• Muita ratkaisuja on. Tällöin sanomme: Vektorit u₁,u₂,...,u_m ovat lineaarisesti riippuvia (LRV)

Pari yksinkertaista havaintoa

Havainto 2. LRT-joukon osajoukko on LRT, LRV-joukon ylijoukko on LRV.
Riittää selvittää vaikkapa jälkimmäinen: Olkoon {a₁,...,a_m} LRV . Tällöin on olemassa kertoimet c₁,...,c_m siten, että

      c1a1 + c2a2 + ... + cmam = 0 

Edellinen seuraa "kontrapositiolla", eli jos LRT joukolla olisi LRV osajoukko, niin tällä LRV-joukolla olisikin LRT ylijoukko, mikä on ristiriidassa edellä osoitetun kanssa.

Lause(LRV1). Vektorit u₁,u₂,...,u_m ovat LRV,
jos ja vain jos
Jokin u_k on muiden lineaarikombinaatio.

Tod. (1) Oletetaan LRV. Tällöin on olemassa kertoimet c₁, ..., c_m, joista jokin # 0, s.e. yhtälö

      c1u1 + c2u2 + ... + cmum = 0 

(2) Käänteinen puoli vastaavasti.

[QED]

Tälle voidaan esittää hieman "terästetty" muoto, joka osoittautuu yllättävän monessa tilanteessa hyödylliseksi työkaluksi.

Lause(LRV2). Järjestetty joukko {v₁,v₂,...,v_n}, missä n > 1 ja v₁ # 0, on LRV
     jos ja vain jos
jokin v_j on edellisten v₁,...,v_j-1 lineaarikombinaatio.

Huom: Tämän avulla on helppo nähdä tietynlaiset "porrasmaiset" vektorijoukot lineaarisesti riippumattomiksi. Jos nimittäin mikään ei ole edellisten lineaarikombinaatio, on tämän perusteella vektorijoukon oltava LRT.

   c1v1 +...+ cnvn = 0 

      c1v1 +...+ cjvj = 0 

Miten selvitetään LRT / LRV Rⁿ:ssä

Esim. Ovatko vektorit

a1 := [3, 0, 2, 2], 
a2 := [-6, 42, 24, 54],
a3 := [21, -21, 0, 15]

LRT / LRV ?

      c1a1 + c2a2 + c3a3 = 0 

No ei muuta kuin kirjoitetaan vektoriyhtälömme komponenttimuodossa

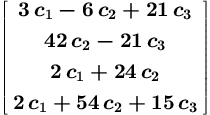
Kysymys on siis yhtälösysteemin Ac = 0 ratkaisuista, missä

                                  [3    -6     21]
                                  [              ]
                                  [0    42    -21]
                             A := [              ]
                                  [2    24      0]
                                  [              ]
                                  [2    54     15]

    (1) Jos on pelkkä 0-ratkaisu (triv. ratk.), niin LRT.
    (2) Jos on muitakin, niin LRV

Nythän meillä on tuo mainio funktio ref,joka saattaa matriisin porrasmuotoon ("Row Echelon Form").

>> A=[3    -6     21;0    42    -21;2    24      0;2    54     15]

A =

     3    -6    21
     0    42   -21
     2    24     0
     2    54    15

>> addpath /home/apiola/opetus/peruskurssi/s03/matlab  
% Tähän oma polkusi, jonka varrelle sijoitit ref.m-tiedoston.

>> ref(A)
ans =

    3.0000   -6.0000   21.0000
         0   58.0000    1.0000
         0         0  -21.7241
         0         0         0

Johtopäätös: LRT

Miten selvitetään LRT / LRV funktioavaruudessa

Esimerkki 1: Monomit ovat LRT

            p(x) = c(x-z0)(x-z1)...(x-zk)

Esimerkki 2: 2 funktiota LRV <=> niiden suhde = vakio

1. Ovatko sin(x) ja cos(x) LRV vai LRT C[0,1]:ssä?
   Olkoon c₁ cos(x) + c₂ sin(x) = 0 kaikilla x välillä [0,1]. Jos c₂#0 , saadaan:

            tan(x)=sin(x)/cos(x) = -c2/c1 = vakio
   

   Tämähän on järjetöntä, joten c₂=0, ja siis myös c₁=0. (Monta muutakin tapaa.)
2. Otsikon julistus osoitetaan aivan samoin todeksi.
3. Funktiojoukko {sin(2t), sint cost} on LRV, koska sin(2t) = 2 sint cost.

Esim. 3 Lisää funktioita

    c1 sin2 x + c2 cos 2x + c3 = 0

   (c1-2c2)sin2 x + c2 + c3 = 0

              c1 - 2 c2 = 0
              c2 + c3   = 0

Siis ovat LRV.

Funktiojoukon osoittaminen LRT:ksi

Esim: Funktiot 1,e^x, e^-x avaruudessa C[-1,1].
Olkoon

          c1 + c2 ex + c3 e-x = 0 kaikilla x välillä [-1,1]

          | 1  1/e   e  | |c1| 
          | 1   1    1  | |c2| = 0
          | 1   e   1/e | |c3|

>> e=exp(1)               

e =

    2.7183

>> A=[1 1/e e;1 1 1;1 e 1/e] 

A =

    1.0000    0.3679    2.7183
    1.0000    1.0000    1.0000
    1.0000    2.7183    0.3679

>> addpath /home/apiola/opetus/peruskurssi/s03/matlab
>> ref(A)                                            

ans =

    1.0000    0.3679    2.7183
         0    2.3504   -2.3504
         0   -0.0000   -1.0862

Huomataan, että myös funktioiden LRT-kysymys johtaa tapauksessa,jossa asia ei ole muuten ilmeinen, lineaariseen yhtälösysteemiin. (Kaikki tiet vievät ref:iin!)

Huom: Tällä kurssilla funktioiden LRT/LTV-asiat tulevat vastaan erityisesti lineaaristen differentiaaliyhtälö(systeemien) puolella.

Kanta(basis) ja dimensio

Määritelmä. Vektoriavaruuden V kanta on vektorijoukko {e₁,e₂,...,e_m}, joka

   1. on LRT
   2. virittää V:n

Lause 1 Jos {e₁,e₂,...,e_m} on V:n kanta, niin jokaisella vektorilla v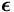V on yksikäsitteinen esitys muodossa

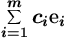
Tod: Olkoon vektorilla v kaksi esitystä:

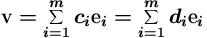
Siis

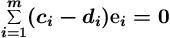
Niinpä kertoimien samuus seuraa kantavektorien LRT:sta.
[QED]

Tod: Olkoot {u₁,...,u_m} ja {v₁,...,v_n} V:n kantoja. Tehdään vastaoletus: n > m.

Jotta asia näkyisi mahdollisimman pelkistetysti, laskemme tapauksen, jossa m=2 ja n=3. Yleisen todistuksen perusjuoni paistaa tästä oikein hyvin.

Avaruudella V on siis kannat: {u₁,u₂} ja {v₁,v₂,v₃}.

No, koska u-vektorit virittävät, voidaan v:t esittää:

      v1 = a u1 + b u2
      v2 = c u1 + d u2
      v3 = e u1 + f u2

     c1 v1 + c2 v2 + c3 v3 = 0

                      [a    c    e][c1]
                      [           ][c2] = 0
                      [b    d    f][c3]

Tässä meillä on homogeeniyhtälö, jossa on enemmän sarakkeita kuin rivejä. Niin ollen sillä on ei-triviaaleja ratkaisuja, ja niinpä v-vektorit ovat LRV. Päädyimme ristiriitaan, joten erilukumääräiset kannat eivät ole mahdollisia.

[QED]

Korostetaan vielä: Lauseen 2 mukaan määritelmä on "hyvin asetettu", eli siinä on mieli.

Huom! Todistimme yllä itse asiassa seuraavan:

Lause 2' Jos {u₁,...,u_m} virittää ja {v₁,...,v_n} on LRT, niin n <= m. Toisin sanoen: mielivaltainen LRT joukko on jokaista virittävää joukkoa pienempi (tai yhtäsuuri).

Olisi peräti merkillistä, ellei pätisi:

Lause 3. Avaruus Rⁿ on n-ulotteinen.

Tod. Luonnolliset koordinaattiyksikkövektorit e₁=(1,0,...,0), e₂=(0,1,0,...,), e_n=(0,0,...,1) ovat LRT ja virittävät. (Osaathan perustella!) Väite seuraa siis dimension määritelmästä.

Olkoon

>> B=[1 4 0 2 0;0 0 1 -1 0;0 0 0 0 1;0 0 0 0 0 ]

B =

     1     4     0     2     0
     0     0     1    -1     0
     0     0     0     0     1
     0     0     0     0     0

   b4  = 2 b1 - b3

No konstikos tuo nyt oli, kun matriisi oli rref-muodossa, voisi joku huomauttaa! Myöhemmin nähdään, että esimerkki on sittenkin varsin edustava, tarvitsee vain ensin osoittaa tietyt säilyvyysasiat Gaussin rivioperaatioissa.

Sarakeavaruuden yleinen käsittely herättää yleisen kysymyksen: Jos on määrättävä annettujen vektorien virittämän aliavaruuden kanta, voidaanko kantavektorit valita virittäjävektorien joukosta, ts. saadaanko kanta siten, että pudotetaan vain pois sopiva määrä riippuvia "redundantteja" virittäjävektoreita. No näinhän toki on, ja perustelukin on hyvin yksinkertainen:

Kannaksi laajentaminen ja karsiminen

Molempien prosessien induktioaskel perustuu hyvin yksinkertaiseen tosiasiaan:

Lemma 1 (LRT-lemma) jos vektorijoukko {u₁,...,u_d} on LRT ja jokin vektori v ei ole näiden lineaarikombinaatio, niin joukko {u₁,...,u_d,v} on LRT.
Tod:
Muodostetaan vektoriyhtälö

   c1u1+...+cdud + c v = 0.

[QED]

Lause (Kannaksi laajentaminen)
Olkoon V äärellisulotteinen vektoriavaruus, jonka dimensio = n. Mielivaltainen V:n LRT vektorijoukko {v₁,...,v_k} voidaan laajentaa V:n kannaksi.

Tod: Jos joukko virittää, niin se on kanta (jolloin on oltava k=n). Ellei, niin on olemassa vektori v_k+1, joka ei ole edellisten lineaarikombinaatio. Lemman mukaan joukko {v₁,...,v_k,v_k+1 } on LRT.
Jos se virittää, niin se on kanta, muussa tapauksessa jatketaan, kunnes on saatu n:n vektorin LRT joukko. Sen on pakko virittää, sillä yksi lisäaskel johtaisi ristiriitaan kantalauseen (version 2') kanssa.
[QED]

Virittävän joukon karsiminen kannaksi menee saman induktioaskeleen avulla, vaikka näin:

Lause (Kannaksi karsiminen)
Olkoon V = sp({v₁,...,v_m}). Tällöin jokin virittäjäjoukon osajoukko on V:n kanta. (Ts. pudottamalla sopivat vektorit pois, saadaan kanta.)

Tod. Olkoon d = max määrä LRT vektoreita virittäjäjoukossa Numeroidaan vektorit niin, että {v₁,...,v_d} ovat LRT, jolloin loput ovat lausuttavissa näiden lineaarikombinaatioina. Ellei nimittäin joku olisi, niin lemman mukaan tämä yhdessä v₁,...,v_d - vektorien kanssa muodostaisi LRT joukon, vastoin d:n maksimaalisuutta. Näin ollen vektorit {v₁,...,v_d} virittävät saman kuin vektorit {v₁,...,v_m} , eli koko avaruuden V. (koska lineaarikombinaatioden lineaarikombinaatio on alkup. vekt. lin. komb.). Siten {v₁,...,v_d} on V=sp({v₁,...,v_m}):n LRT ja virittävä joukko, eli kanta.

Huomautus matriisin sarakeavaruudesta Edellä laskimme erään matriisin sarakeavaruuden kannan. Havaitsimme, että tukisarakkeet muodostivat maksimaalisen LRT-joukon sarakevektoreiden parissa. Lausemme sanoo, että tämä on yleispätevä menettely. Palaamme asiaan vielä lähemmin seuraavassa luennossa (LA3), jossa käsitellään matriisiin liittyviä luonnollisa vektoriavaruuksia: nolla-avaruutta (N(A)), riviavaruutta row(A) ja sarakeavaruutta col(A).

Funktioavaruuksien kantoja, erityisesti polynomit

Niinpä siis yleisesti monomit 1, x,...,xⁿ muodostavat polynomiavaruuden P_n kannan, ja siis sen dimensio = n+1.

Äärellisulotteinen/ääretönulotteinen avaruus

Toisaalta, jos avaruudessa on äärellinen yläraja LRT vektorien lukumäärälle, niin siinä on siis LRT joukko, jota suuremmat joukot ovat LRV, ja siten (kantalauseen perusteella) tällainen maksimaalinen LRT joukko on kanta.

Määritelmä Vektoriavaruus V on äärellisulotteinen, jos LRT vektorien lukumäärällä on äärellinen yläraja. Muussa tapauksessa V on ääretönulotteinen.

Lause 5. Jos vektoriavaruuden V on äärellisulotteinen, niin sillä on kanta. V:n dimensio = maksimimäärä LRT vektoreita (eli pienin edellä mainittu yläraja).

Tod: Olkoon n tuo maksimimäärä. Tällöin siis on olemassa LRT vektorit b₁,...,b_n ja jokainen (n+1):n vektorin joukko on LRV. No, jos otamme mielivaltaisen vektorin v avaruudesta V, niin joukko {b₁,...,b_n,v} on LRV, Lemman mukaan (jälleen kerran) päätellään, että v on b-vektorien lineaarikombinaatio, ja siten {b₁,...,b_n} myös virittää ja on siis kanta.

[QED]

Onko ääretönulotteisia avaruuksia olemassa? Onko insinööreillekin? No on on ja paljon !!
Tulemme näkemään monia funktioavaruuksia tämänkin kurssin kuluessa. Yleensä funktioavaruudet ovat miltei poikkeuksetta ääretönulotteisia.

Esimerkkejä funktio- ja jonoavaruuksista

• Polynomiavaruus P on ääretönulotteinen.
  Perustelu: P:ssä on miten suuria LRT joukkoja hyvänsä, nimittäin monomit 1,x,x²,..., xⁿ, olipa n miten suuri luku hyvänsä.
• Avaruus C[a,b] sisältää aliavaruutenaan P[a,b]:n , joten ensinmainittu on varmasti ääretönulotteinen. Itse asiassa useimmat vastaan tulevat funktioavaruudet sisältävät polynomit, joten tässä heti perustelu sille (hieman väljälle) lausumalle, jonka yllä esitimme.
• Kaikkien (äärettömien) jonojen avaruus S on ääretönulotteinen.
  Perustelu: Jonot e₁=(1,0,0,...), e₂=(0,1,0,...), ..., e_k=(0,0,...,1,0,...), ... muodostavat äärettömän jonon vektoreita S:ssä. Mikä tahansa äärellinen määrä näitä vektoreita on LRT, vaikkapa LRV-lemman perusteella tai suoraan LRT-määritelmästä.

  Useimmat S:n kiintoisat aliavaruudet sisältävät nämä vektorit, ja ovat siten myös ääretönulotteisia.
  Tämä voidaan ymmärtää myös Rⁿ:n yleistyksenä. Kun S:ssä on äärettömän monta koordinaattia, niin dim S on ääretön. (Vastaavasti Rⁿ:ssä on n koordinaattia ja dim Rⁿ = n .)