file: ./L/LA1.html   Päivitetty 17.9.03 HA

Lineaarialgebran luento LA1

Matriisit ja lineaariset yhtälösysteemit, Matlab-perusteita

1. Matriisialgebraa

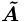
Kertaa KRE8 6.1 - 6.2 Matriisitulo, Transpoosi AT (Matlab: A' ), Yksikkömatriisi Id:=diag(1,1,...1) (Matlab-notaatio: diag(ones(n)) ).

Matriisien käsittely Matlab:lla

Matlabin perusteita voit myös opiskella näistä:
Lyhyt Matlab-opas
"Ei-niin-lyhyt" Matlab-opas

Ensimmäinen Matlab-esimerkki 

>> A=[1 2 3 4;5 6 7 8;9 10 11 12]
A =
     1     2     3     4
     5     6     7     8
     9    10    11    12
  
>> B=A'
B =
     1     5     9
     2     6    10
     3     7    11
     4     8    12

>> C=A*B
C =
    30    70   110
    70   174   278
   110   278   446
Matlab:ssa ei tarvita loppumerkkiä. Jos tulostus halutaan estää, lopetetaan puolipisteeseen (;) Matlab käsittelee vain numeerisia matriiseja, mutta niitä sitten tehokkaasti.

Symbolisessa muodossa operointi ei ole mahdollista (symbolic toolbox laajentaa tähän suuntaan, mutta sitä emme tässä käsittele). Rationaaliaritmetiikkaa voidaan käyttää komennolla 

 format rational

2. Lineeriset yhtälösysteemit, Gaussin eliminaatio

KRE 6.3 s. 321 ... (Kertausta peruskurssien 1 asioista.) 

   A x =b, missä
     A on kerroinmatriisi (m x n) (m yhtälöä, n tuntematonta)
     x on tuntemattomien muodostama sarakevektori     (n x 1)
     b on annettujen lukujen muodostama sarakevektori (m x 1)
Ratkaisujen lukumäärä voi olla 0, 1 tai ääretön, kuten jo 2 x 2 systeemeistä tiedetään (yhdensuunt. suorat, leikkaavat suorat, yhtyvät suorat).

Riviajattelu: Suorien leikkauspiste
Sarakeajattelu: Etsitään annetun vektorin (b) koordinaatit matriisin sarakevektorien avulla esitettynä. (Puhutaan luennolla.)

Gaussin eliminaatio, s. 321

Alkeisrivioperaatiot (s. 326) 

   1. rivi[i] <-->  rivi[k]  (rivien vaihto)
   2. rivi[i] <--  c*rivi[i] , c ei ole 0
   3. rivi[i] <--  rivi[i]+c*rivi[k] , c ei ole 0
Rivioperaatioissa yhtälösysteemi säilyy ekvivalenttina (samat ratkaisut). Tähän perustuu ratkaisu Gaussin menettelyllä. Muunnetaan systeemi yläkolmiomuotoon. Rivioperaatiot voidaan helpoimmin kohdistaa suoraan matriisiin, jossa A:n perään liitetään b-sarake. Tätä sanotaan liitännäismatriisiksi, "augmented matrix" . Käytämme merkintöjä Amato tai Ab. [KRE]-kirjassa merkitään:
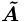
Amato
(Välttelemme liiallisten kuva-kaavojen käyttöä.)

Matlab Rivioperaatiot: 

A([i k],:)=A([k i],:)   
A(i,:)=c*A(i,:)
A(i,:)=A(i,:)+c*A(k,:)

Matlab-esim.

Kuten edellä nähtiin, Matlabissa matriisin A riviin k viitataan lausekkeella A(k,:). Siten kaksoispiste tarkoittaa sitä, että ao. suunnan indeksit käyvät läpi kaikki arvonsa.

Matriiseilla työskentelyyn voit tutustua tarkemmin näistä viitteistä: 

>> A=[1 2 3 4;2 4 8 10; 3 6 11  14];b=[1;1;1];Ab=[A b]

Ab =

     1     2     3     4     1
     2     4     8    10     1
     3     6    11    14     1

>> Ab(2,:)=Ab(2,:)-2*Ab(1,:)

Ab =

     1     2     3     4     1
     0     0     2     2    -1
     3     6    11    14     1

>> Ab(3,:)=Ab(3,:)-3*Ab(1,:) 

Ab =

     1     2     3     4     1
     0     0     2     2    -1
     0     0     2     2    -2

>>  Ab(3,:)=Ab(3,:)-Ab(2,:)  

Ab =

     1     2     3     4     1
     0     0     2     2    -1
     0     0     0     0    -1
Johtopäätös: ei ratkaisuja

Yllä oleva voidaan rakentaa hyvin helposti "puoliautomaattiseksi": Ensimmäisen sarakkeen nollaus: 

[m,n]=size(A)
i=1;j=1;
for k=i+1:m
   A(k,:)=A(k,:)-(A(k,j)/A(i,j))*A(i,:);
end
A
Jatketaan, tässä käyttäjän pitää katsoa, mikä sarake seuraavaksi valitaan. Rivi-indeksi kasvaa yhdellä (tai sitten ollaan lopussa). 
i=i+1; j=...  % j=j+1; tai j+2 tms, käyttäjä asettakoon
for k=i+1:m
   A(k,:)=A(k,:)-(A(k,j)/A(i,j))*A(i,:);
end
A

Katsotaan edellisen esimerkin avulla: 



A=[1 2 3 4;2 4 8 10; 3 6 11  14];b=[1;1;1];Ab=[A b]
[m,n]=size(A);
i=1;j=1;
for k=i+1:m
   Ab(k,:)=Ab(k,:)-(Ab(k,j)/Ab(i,j))*Ab(i,:);
end
Ab
Ab =
      1            2            3            4            1      
      0            0            2            2           -1      
      0            0            2            2           -2  

i=i+1; j=3
for k=i+1:m
   Ab(k,:)=Ab(k,:)-(Ab(k,j)/Ab(i,j))*Ab(i,:);
end
Ab
Ab =
      1            2            3            4            1      
      0            0            2            2           -1      
      0            0            0            0           -1

Gaussin algoritmi

Kun olet hiukan harjoitellut Gaussin eliminaatiota, huomaat, että algoritmi voidaan yleisesti kuvata tähän tapaan.

Askel 1:

  1. Jos a[1,1]=0 ja kaikki sen alapuoliset alkiot ovat = 0, niin 1. sarake on 0-sarake. Jatketaan oikealle, kunnes tulee nollasta erillinen sarake vastaan tai ollaan lopussa ja meillä on 0-matriisi, jolloin lopetetaan.
    Edellisessä tapauksessa vaihdetaan tämä sarake ensimmäiseksi ja siirrytään kohtaan 2. (Sarakkeen vaihdot tehdään teoreettisessa algoritmissamme, käytännössä ei.)
  2. a[1,1] tai jokin sen alapuolinen alkio on # 0, suoritetaan rivinvaihto. (Jos on valinnanvaraa, vaihdetaan ensimmäiseksi se, jossa on suurin "PIVOT".) Valitaan kertoimet c[2]=-a[2,1]/a[1,1],...,c[m]=-a[m,1]/a[1,1] ja suoritetaan rivioperaatiot:

    rivi[2] <-- c[2]*rivi[1] + rivi[2]
    ...
    rivi[m] <-- c[m]*r[1] + r[m]

    Näin saadaan alkion a[1,1]#0 alle 0-sarake.

Askel 2:
  1. Jos a[2,2]=0 ja kaikki sen alapuoliset alkiot ovat = 0, niin kaikki on hyvin. Tällöin syntyy "pitkä porras" ja siirrytään katsomaan samalla silmällä a[2,3]:a ja sen alapuolista saraketta.
    Jos tämän suhteen käy samoin, siirrytään taas eteenpäin.
    Jos ajaudutaan loppuun (sarakkeeseen n) samoin tuloksin, on kaikki alapuolinen 0:aa ja olemme lopussa.
    Ellei ajauduta loppuun, löytyy nollasta poikkeava "ala"sarake. Teoreettisessa algoritmissamme vaihdamme tämän sarakkeen 2. sarakkeeksi, käytännössä emme vaihda sarakkeita, vaan annamme syntyä pitkiä portaita.
  2. a[2,2] tai joku sen alapuolella #0, vaihdetaan (tarvittaessa) rivit, niin, että uusi a[2,2] # 0. (Numeerisessa käytännössä vaihdetaan itseisarvoltaan mahdollisimman suuri.) Sitten jatketaan kohdasta [2,2] alkavalle alimatriisille samoin kuin Askel 1:ssä.
Näin jatketaan niin kauan, kunnes tullaan riville r, jonka alapuolella kaikki on nollaa tai tullaan riville m, eli r=m.

Yllä kuvattu algoritmi voidaan kirjoittaa helposti Matlabilla toimivaksi ohjelmaksi. Matlabin kyky käsitellä kokonaisia vektoreita ja niiden osia tekee tällaisen algoritmin ohjelmoinnin varsin helpoksi. Edellähän jo esitimme "laajennettuun käsinlaskuun" hyvin sopivan version.

Tässä on funktio ref. Se on tyylikäs toteutus, jonka kirjoitin Matlabin omaa rref-funktiota hiukan modifioimalla (riisumalla). Matlab-lukutaitoinen henkilö näkee helposti, miten koodi toimii. Kannattaa verrata edellä olevaan algoritmin kuvaukseen.

Voit ottaa ref-funktion itsellesi. Matlab löytää sen polun varrelta. Anna sopiva addpath-komento Matlabissa.

Ohje harjoituksia varten

Luokassa kannattaa tehdä hakemisto z:\matlab Sinne voi kerätä hyödyllisiä omia tai saatuja Matlab-funktioita. Polku on sitten syytä asettaa joko valikosta tai 
   addpath z:\matlab

Joitakin esimerkkejä 

A= [7 -9 -4  5  3 -3 -7;
   -4  6  7 -2 -6 -5  5;
    5 -7 -6  5 -6  2  8;
   -3  5  8 -1 -7 -4  8;
    6 -8 -5  4  4  9  3]

A =

     7    -9    -4     5     3    -3    -7
    -4     6     7    -2    -6    -5     5
     5    -7    -6     5    -6     2     8
    -3     5     8    -1    -7    -4     8
     6    -8    -5     4     4     9     3

>> ref(A)

ans =

    7.0000   -9.0000   -4.0000    5.0000    3.0000   -3.0000   -7.0000
         0    1.1429    6.2857    1.1429   -5.7143   -5.2857    5.0000
         0         0         0    2.0000  -11.0000    1.5000   15.5000
         0         0         0         0         0   10.2500   10.2500
         0         0         0         0         0         0         0

%        x         x                 x                    x
Merkitsimme "x":llä "johtavat sarakkeet" eli "tukisarakkeet", eli ne, joissa oli nollasta poikkeava "aloitusalkio" mahd. rivinvaihdon jälkeen. Tukisarake on siten sellainen sarake, jolla esiintyy (jonkin) rivin ensimmäinen 0:sta poikkeava alkio.

Alla olevassa teoreettisessa muodossa on siirrety kaikki tukisarakkeet vasemmalle ja loput oikealle. Se helpottaa hiukan teoreettisten johtopäätösten tekoa, mutta algoritmi, joka myös laskee ratkaisut (kun niitä on), ei sarakevaihtoja tee.

Porrasmuoto, Echelon form

Gaussin algoritmi johtaa aina muotoon: (Merkinnät KRE-kirjan mukaiset) KRE 8 s. 329. 

   a1,1  a1,2       ...           a1,n   b1
     0     c2,2       ...        c2,n   bmato2
     0       0
     0       0
     
     

     0       0   0.. 0  kr,r ... kr,n   bmator
     0       0   0.. 0    0  .. 0     bmator+1

     0       0   0.. 0    0  .. 0     bmatom
Tässä "päälävistäjän" alkiot a1,1, c2,2, ..., kr,r ovat nollasta poikkeavia.

Tämä muoto, kuten sanottu, saadaan siis aikaan sarakevaihtojen avulla. Tästä voidaan vaivattomimmin tehdä teoreettiset, ratkaisujen olemassaoloa ja lukumäärää (vapaiden parametrien lukumäärää) koskevat johtopäätökset.

Ratkaisujen olemassaolo ja lukumääräkysymykset ovat kaikki luettavissa tästä kaaviosta. Saamme peruslauseen

Lause, LINYHT: Lineaaristen yhtälösysteemien peruslause
(a) r < m ja jokin bmatoi # 0, r+1 <= i <= m == > Ei ratk.
(b) r=n ja bmatoi=0, i=r+1 .. m (tai nämä (i > r)bmadot puuttuvat (tap. m=n)) ==> yksikäs. ratk.
(c) r < n ja bmatoi=0, i=r+1 .. m (tai "kriittiset" bmadot puuttuvat (tap. m < n ja r = m) ) ==> äärettömän monta ratkaisua

Tyyppiesimerkit

Koska Matlab ei ole symbolinkäsittelyohjelma (paitsi "symbolic toolbox"), teemme ensimmäisen esimerkin Maplella. (Helppoa vaikka käsin.) Haluamme nimittäin jättää yhden vapaan parametrin b-vektoriin. Symboliominasiuutta tarvitaan vain 1. esimerkissä. Toinen syy on se, että Matlabissa ei ole valmiina funktiota ref, joka suorittaisi vain Gaussin rivioperaatiot yläkolmiomuotoon saakka. Siinä on rref, jota emme tässä vaiheessa halua vielä ottaa esille.

Tapaukset (a) ja (c)

(Maplen syntaksi, vanha "linalg"-tyyli, lienee helppo lukea, mitä tehdään.) 
> with(linalg):
> A:=matrix(3,3,[2,1,-2,1,2,1,3,3,-1]);
                                   [2    1    -2]
                                   [            ]
                              A := [1    2     1]
                                   [            ]
                                   [3    3    -1]
> b:=vector([4,4,c]);
                                b := [4, 4, c]
> Ab:=augment(A,b);
                                 [2    1    -2    4]
                                 [                 ]
                           Ab := [1    2     1    4]
                                 [                 ]
                                 [3    3    -1    c]
> ylakolmio:=gausselim(Ab);
                                 [2     1     -2      4  ]
                                 [                       ]
                    ylakolmio := [0    3/2     2      2  ]
                                 [                       ]
                                 [0     0      0    c - 8]
m=n=3, r=2
Lasketaan loput Matlabilla, kun meillä on tuo maanmainio ref-funktio käytössämme.

Tapaus (b), yksikäs. ratk. 


>> A=[1 1 -1;3 1 1;1 -1 4] 

A =

     1     1    -1
     3     1     1
     1    -1     4

>> b=[1;9;8]

b =

     1
     9
     8

>> Ab=[A b]

Ab =

     1     1    -1     1
     3     1     1     9
     1    -1     4     8

>> ref(Ab)

ans =

    3.0000    1.0000    1.0000    9.0000
         0   -1.3333    3.6667    5.0000
         0         0    0.5000    0.5000

>> E=ref(Ab)

E =

    3.0000    1.0000    1.0000    9.0000
         0   -1.3333    3.6667    5.0000
         0         0    0.5000    0.5000
m=n=r=3 Jokainen kerroinmatriisin sarake on tukisarake, takaisinsijoituksella 1-käs ratkaisu.

Tapaus (c), toinen esimerkki, jossa äärettömän monta ratkaisua, tällä kertaa 2 vapaata muuttujaa (vrt. (a)) 

>> A=[1,-1,1,0,0,2;1,1,2,4,1,2;0,2,1,4,3,1;1,-3,0,-4,-2,1]

A =

     1    -1     1     0     0     2
     1     1     2     4     1     2
     0     2     1     4     3     1
     1    -3     0    -4    -2     1

>> b=[0; 3; 2; 0]

b =

     0
     3
     2
     0

>> Ab=[A b]

Ab =

     1    -1     1     0     0     2     0
     1     1     2     4     1     2     3
     0     2     1     4     3     1     2
     1    -3     0    -4    -2     1     0

>> E=ref(Ab)

E =

    1.0000   -1.0000    1.0000         0         0    2.0000         0
         0    2.0000    1.0000    4.0000    1.0000         0    3.0000
         0         0         0         0    2.0000    1.0000   -1.0000
         0         0         0         0         0   -0.5000    2.5000

%        x         x                            x        x

% Merk. (A:n) tukisarakkeet x:llä
m=4,n=6,r=4=m < n Kriittiset (siis i > r) bmadot puuttuvat, ääretön määrä (tarkemmin (n-r)=2-parametrinen joukko) ratkaisuja.
Nähdään myös (kuten aina) suoraan takaisinsijoitusta tehtäessä (tai ajateltaessa tehtäväksi). 

   4. rivi => x6 yksikäs.
   3. rivi => x5 yksikäs.
   2. rivi :  x4 ja x3 vapaiksi param. => x2
   1. rivi => x1 yksikäs, kun yo. vapaat parametrit on kiinnitetty.
Tai nähdään siitäkin, kun tukisarakkeet rastitetaan ja lasketaan n-(rastien lkm) = 2

Havainnollistus

Tapaus a) r < m ja B2 # 0 

  a)   r < m  ja B2 # 0
                       n                          n
      ------------------               ----------
     |                 |  |            |        |  |
     |                 |  | B1         |        |  | B1                  |  |            |        |
     |                 |  |            |        |  |
  r   ------------------             r ----------
     |  0 ...       0  |  | B2         | 0..0   |  | B2
     |  0 ...       0  |  |            | 0..0   |  | 
  m   ------------------             m ----------
Saadaan ristiriitainen yhtälö 0=B2(i) jollain i. Ei ratkaisuja

Tapaus b) r = n ja (B2 = 0 tai puuttuu)

(B2 puuttuu <==> r=m, joten tässä puutostilanteessa r=n=m) 

                       n       
     -------------------
     |                 |  |
     |                 |  |            
     |                 |  | B1         
     |                 |  |            
     |                 |  |
     |                 |  |
  r   ------------------             
     |  0 ...       0  |  0 B2    Tämä siis voi puuttua,    
     |  0 ...       0  |  0       jolloin m=r=n     
  m   ------------------
Yksikäsitteinen ratkaisu. Tällöin porrasmuoto on joka kohdassa "yksiaskelinen". Takaisinsijoitusvaiheessa jokaisessa yhtälössä yksi uusi tuntematon. Siis todellakin yksikäs. ratkaisu.

Tapaus c) r < n ja (B2 = 0 tai puuttuu)

(B2 puuttuu <==> r=m) 

                     r    n       
     ----------------------
     |               |    |  |            
     |               |    |  | B1         
     |    Er x r      | P  |  |           Er x r   
     |               |    |  |      on yläkolmiomatriisi, jonka 
     |               |    |  |      päälävistäjän alkiot # 0
  r   ---------------------             
     |  0 ...       0| 0  |  0 B2    Tämä voi puuttua.    
     |  0 ...       0| 0  |  0      
  m   --------------------
Ääretön määrä ratkaisuja, n-r vapaata parametria.

Seurauslause homogeenisille systeemeille A x = 0

Lause (HOMYHT): Homogeeninen yhtälösysteemi

Jos homogeeniyhtälössä A x = 0 on m < n , niin aina on äärettömän monta ratkaisua.

Tod:Tällöinhän bmato=0 ja r <=m < n .

3. Gauss/Gauss-Jordan, ref/rref

AG s. 60, KRE s. 350 (KRE:ssä vain neliömatr., käänteismatriisin laskemisen yhteydessä.)

Määritellään nyt tarkemmin, mitä tarkoitamme ref:llä ja rref:llä.

Takaisinsijoitus voidaan myös toteuttaa rivioperaatioina, jolloin päädytään muotoon, josta ratkaisut ovat luettavissa vielä suoremmin kuin alakolmiomuodosta. Siitä käytetään nimitystä redusoitu porrasmuoto, "reduced row echelon form" (siitä lyhenne rref, jota mekin käytämme). Tässä nollataan myös yläkolmio johtavien sarakkeiden (tuki- eli pivot-) sarakkeiden) osalta. (Palataan yksityiskohtiin myöhemmin.) Ei-singulaarisen neliösysteemin tapauksessa päädytään diagonaalimatriisiin. Matlab-funktio rref, jota jo yllä katselimme, tekee tämän.

Prosessia, jolla rref-muoto saadaan aikaan, kutsutaan Gauss-Jordanin menetelmäksi. (ref-muotohan syntyy Gaussin eliminaatiomenettelyllä.)
Tämä on erityisen hyödyllinen tapa silloin, kun on laskettava annetun neliömatriisin käänteismatriisi. (Tätä siis KRE käsittelee, palataan.)

Määritelmät ja yhteenvedot aiheista ref/rref

Kootaan ja täsmennetään vielä edellä selostettua:

Sanonta: Nollasta poikkeavan rivin 1. nollasta poikkeava alkio on nimeltään johtava alkio ("leading entry"), tai tukialkio ("pivot"). Johtavan alkion määräämää saraketta sanotaan johtavaksi sarakkeeksi , eli pivot- eli tukisarakkeeksi.

Määritelmä: ref ja rref
Matriisi on ref-muodossa, jos

  1. Nollarivit ovat pohjalla. (Kaikki nollasta poikkeavat rivit ovat jokaisen nollarivin yläpuolella.)
  2. Jokaisen ei-nollarivin johtava alkio on yläpuolella olevan rivin johtavan alkion oikealla puolella (aidosti).
  3. Johtavan alkion määräämän sarakkeen alaosa (johtavan alkion alapuoli) koostuu nollista.

    Redusoitua porrasmuoto, rref on sellainen ref-muoto, jossa lisäksi

  4. Johtavat alkiot ovat ykkösiä,
  5. Johtavat sarakkeet ovat nollia myös johtavan alkion yläpuoliselta osalta. (Ts. johtavat sarakkeet ovat yksikkömatriisin sarakkeita.)
Esim: Kaikki nämä matriisit ovat rref-muodossa, johtavat sarakkeet on merkitty *:llä. 
 *    *    *       *    *            *         *
[1    0    0]     [1    0    2]     [1    5    0    0]
[           ]     [           ]     [                ]
[0    1    0]     [0    1    6]     [0    0    1    2]
[           ]     [           ]
[0    0    1]     [0    0    0]     [0    0    0    0]
                                    [0    0    0    0]
     *         *    *    *
    [1    1    0    0    0     6]
    [                           ]
    [0    0    1    0    0    -1]
    [                           ]
    [0    0    0    1    0     3]
    [                           ]
    [0    0    0    0    1     1]
Tämä kuuluu osata, vaikka ei olekaan KRE:ssä.

ref vai rref ?

Käytännön laskennassa on edullisempaa käyttää ref-muotoa (siis yläkolmiota), sillä takaisinsijoitus on halvempaa kuin rivioperaatiot. Teoreettisesti rref-muoto on kauniimpi, sitä on siten sopivaa käyttää johtopäätösten tekoon (Johtopäätökset voidaan lukea helposti myös ref-muodosta.)

Myös yhtälösysteemin muoto, josta ratkaisujen olemassaolo- ja lukumäärätieto sadaan luetuksi, on vielä pelkistetympi muodossa: ([AG] s. 60 ..) 

    | Ir  P | b1| 
    | O1  O2| b2|
Tässä Ir on r x r-yksikkömatriisi, P on n x (n-r) - matriisi (Tällä matriisilla ei ole mitään erityistä rakennetta nollien/ei-nollien suhteen.), O1 on (m-r) x r nollamatriisi, O2 on (m-r) x (n-r) nollamatriisi, ja b1 ja b2 ovat vastaavat bmato-vektorin osat. (Vrt. yllä ref-muotokaavioita.)
(Tähän muotoon pääsemiseksi pitää ajatella tarvittaessa tehdyksi sarakepermutaatiot.)

Pivot- eli tukisarakkeet

Kannattaa panna merkille, että rref on yksikäsitteinen, mitä ref ei ole. Jälkimmäinen on selvää jo sen perusteella, että rivin kertominen erilaisilla vakioilla (#0) johtaa toiseen ref-muotoon.
Emme varsinaisesti tarvitse rref:n yksikäsitteisyyttä, vaikka sen osoittaminen onkin aika helppoa (Kts. esim. Lay). Jos joku katselee tarkkaan Matlab-funktioiden ref ja rref kommentteja, on edellisessä "a"-artikkeli ja jälkimmäisessä "the", eikä siis syyttä.

Koska ref:stä rref:iin mentäessä johtavat sarakkeet pysyvät samoina, niin kaikissa ref-muodoissa täytyy olla samat johtavat sarakkeet. (Tämä on helppo päätellä muutenkin.)

Määritelmä, pivot- eli tukisarake: Matriisin A pivot- eli tukisarake on sellainen sarake, joka vastaa rref-muodon johtavaa saraketta.

Siten "pivot"-kohdat ovat samat kaikissa ref-muodoissa ja saadaan siis selville pelkillä Gaussin eliminaatioaskelilla.

Vapaat muuttujat, kantamuuttujat

Matriisin A tukisarakkeita vastaavat muuttujat ovat kantamuuttujia , kaikki muut ovat vapaita muuttujia . Vapaat muuttujat ovat vapaasti valittavia parametreja. Jos rengastat "pivotit", niin kaikki kerroinmatriisin muiden sarakkeiden indeksit ilmaisevat vapaita muuttujia. Jos ristiriitaisia yhtälöitä ei ole, niin siis vapaiden muuttujien lkm = vapaasti valittavien parametrien lkm. (kuullostaa hieman itsestäänselvyydeltä).

LINYHT-lause toisin ilmaistuna

Koska kyseessä on tärkeä lause, kannattaa harjoitella sen lausumista eri tavoilla.
Lause: LINYHT, "pivot-muoto"
  1. Systeemillä A x = b on ratkaisu(ja) (eli se on "konsistentti"),
          jos ja vain jos
    Gaussin rivioperaatioilla ref-muotoon muokatun liitännäismatriisin Amato=[A b] viimeinen sarake ei ole pivot-sarake, ts. ref-muodossa ei esiinny riviä 
         [0,0, ...,0,c],  c#0
  2. Jos systeemi on konsistentti, sillä on
    • yksikäsitteinen ratkaisu, jos ja vain jos jokainen A:n sarake on tukisarake (pivot-sarake).
    • Muussa tapauksessa sillä on äärettömän monta ratkaisua, tarkemmin sanottuna vapaita parametrejä on yksi kutakin ei-pivot-saraketta kohti.
Huom! Välillä puhumme ref(A):sta ja välillä taas ref(Amato):sta ("madosta"). Ole tarkkana sen suhteen, kumpaa tarkoitetaan.

Takaisinsijoitus, redusoitu porrasmuoto

Edellä olemme puhuneet esimerkeissä takaisinsijoituksesta. Yleisesti ottaen sillä tarkoitetaan ref-muotoon saatetusta yhtälöryhmästä alhaalta ylös edeten tapahtuvaa peräkkäistä ratkaisemista.

Esim

Systeemin liitännäismatriisi olkoon saatu ref-muotoon: Rastitetaan tukisarakkeet: 

         x   x       x
         1  -7   2  -5   8 | 10
         0   1  -3   3   1 | -5
         0   0   0   1  -1 |  4
Vapaat muuttujat ovat x_5 = s ja x_3 = t (merkittiin selvyyden vuoksi uusilla symboleilla). Alimmasta ylimpään edeten: 
        x_4 = x_5+4 = s + 4
        x_2 = 3 t -3 x_4 -s -5 = 3 x_3 - 4 s - 17
        x_1 = ... = 19 t - 31 s - 89
Ratkaisu voidaan kirjoittaa vektoriksi: 
      | 19t - 31s - 89 |    |19 |    |-31|   |-89|
      |  3t - 4s  - 17 |    | 3 |    |-4 |   |-17|
   x= |   t            | = t| 1 | + s| 0 | + | 0 | 
      |        s + 4   |    | 0 |    | 1 |   | 4 |
      |        s       |    | 0 |    | 1 |   | 0 |
(Tarkista ja kerro, jos on virheitä.)

Redusoitu porrasmuoto rref

Taksinsijoituksen sijasta voitaisiin ref-muodosta jatkaa rivioperaatioita alhaalta ylös tavoitteena kunkin tukisarakkeen yläpuolenkin nollaus.

Algoritmi ref-muodosta rref-muotoon.

  1. Normeeraus: Jaetaan kukin tukirivi tukialkiolla, jolloin uudet tukialkiot saadaan ykkösiksi.
  2. Edetään alhaalta ylöspäin nollaten tukialkiolla 1 kunkin tukisarakkeen yläosa.
Jatketaan edellistä esimerkkiä 
>> format compact

>> E=[1  -7   2  -5   8  10;
      0   1  -3   3   1  -5;
      0   0   0   1  -1   4]

>> RE = E   % RE:tä ruvetaan "möyssäämään", pidetään alkup. 
            % E tallessa pahan päivän varalle.
% Sarake no 4:
% ------------
>> RE(2,:)=RE(2,:)-3*RE(3,:); RE  
RE =
      1         -7          2         -5          8         10      
      0          1         -3          0          4        -17      
      0          0          0          1         -1         4  

>> RE(1,:)=RE(1,:)+5*RE(3,:); RE
RE =
      1         -7          2          0          3         30      
      0          1         -3          0          4        -17      
      0          0          0          1         -1          4
Hyväpä hyvä, siirrytään sarakkeeseen 2. 

>> RE(1,:)=RE(1,:)+7*RE(2,:); RE
RE =
      1          0        -19          0         31        -89      
      0          1         -3          0          4        -17      
      0          0          0          1         -1          4    
      
      x          x                     x
Tukisarakkeet ovat nyt yksikkömatriisin sarakkeita. Nyt voimme kirjoittaa ratkaisun suoraan vaikka ylhäältä aloittaen, ylempi tulos ei enää riipu alemmasta. 
   x1 = 19x3 -31x5 - 89
   x2 = 3x3  -4x5  -17
   x4 = x5 + 4

ref- ja rref-muodot Matlabilla

Muistutamme tässä vain referenssin vuoksi vielä yllä esiintyneistä Matlab-funktioista ref ja rref. Jälkimmäinen on Matlabiin kuuluva funktio (jonka lähdekoodi on avoin), edellinen on HA:n tekemä modifikaatio (yksinkertaistus) jälkimmäisestä.

Käytännön laskentaan liittyviä huomioita

Kun algoritmeja implementoidaan tietokoneohjelmiksi, täytyy kiinnittää huomiota (a) numeerisen laskennan virhelähteisiin ja (b) laskennan tehokuuteen, eli aritmeettisten operaatioiden lukumäärään.

Pyöristysvirheet

Jos tukialkio on pieni, joudutaan jakamaan pienellä luvulla, tämä aiheuttaa suhteellisen tarkkuuden huononemista, joka voi olla fataalia. Ensimmäinen periaate on, että rivinvaihtostrategia suoritetaan valitsemalla itseisarvoltaan suurin tukialkio. (Tähän liitetään "oikeissa" algoritmeissa vielä skaalaus.)

Häiriöaltis tehtävä

Jos kaksi suoraa on melkein yhdensuuntaiset, niiden leikkauspisteen määrääminen käy hyvin epätarkaksi. Tämä ajatus voidaan yleistää, mutta sitä ennen tarvitaan joitakin työkaluja, kuten matriisinormia. Näistä myöhemmin.

Tehokkuus

Esitetään yksinkertaisuuden vuoksi n x n - neliömatriisille A 
>> N=[10 100 1000];
>> format bank
>> 2/3*N.^3   

ans =

        666.67     666666.67  666666666.67

>> N.^2       

ans =

        100.00      10000.00    1000000.00
>> format     
>> 2/3*N(3).^3

ans =

   6.6667e+08
>> 2/3*N(3)^3/N(3)^2

ans =

  666.6667   % Jos n=1000, niin rref:iin siirtyminen 
             % vie n. 700-kertaisen ajan.
Palataan rref-algoritmiin käänteismatriisin yhteydessä. Se on siinä varsin näppärä ja sen vaatima aika on puolestaan miljoonasosa vuosia (kohtuullisella n:llä) verrattuna ns. Cramerin sääntöön.

Finaali

Gaussin algoritmi ja siitä johdetut muodot ovat kahdella tavalla merkittäviä:
  1. Teoreettinen näkökulma: Hiukan kärjistäen voidaan sanoa, että koko äärellisulotteisten vektoriavaruuksien teoria "voidaan lukea" yllä olevista ref ja rref-muodoista tavalla tai toisella.
  2. Käytännöllinen näkökulma: Gaussin algoritmi on lähtökohtana kaikille numeerisen lineaarialgebran laskenta-algoritmeille.
Huokaus: Voiko teoria ja käytäntö kauniimmin kohdata!!
This page created by mailto:Heikki.Apiola@hut.fi