
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Tehtäviä MATLAB-opiskelun alkuun ja perusteiden opetteluun.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mlP001.tex
Matlab-pikaohje
- 1.
- Komennon suorittama tulos tulee ruudulle ENTER-painalluksen jälkeen (kuvat erilliseen ikkunaan). Jos haluat estää tulostuksen, päätä komento puolipisteeseen. Jos myöhemmin haluat katsoa muuttujan sisällön, kirjoita sen nimi (ilman puolipistettä). Jos muuttuja on suuri matriisi, kannattaa ensin katsoa sen koko size(A) tai sen jotain osaa, esim. A(1:10,1:10). Tai klikkaa “workspace”-ikkunan muuttujaikonia.
- 2.
- Edellisen komennon tulos on muuttujassa ans. Yleensä on suositeltavaa antaa tulokselle oma nimi tyyliin nimi= ...
- 3.
- Nuoliylös-näppäimellä (↑) voi selata aikaisempia komentoja. Käytä ahkerasti komentoja help, doc.
- 4.
- format long : Tulostetaan enemmän numeroita (n. 16). Laskutarkkuuteen
tämä ei vaikuta.
format rational laskee rationaaliluvuilla.
format short: Paluu oletustulostukseen. - 5.
- Matriisi saadaan aikaan tyyliin: A=[2 4 3;0 1 -1;3 5 7]. Vektori saadaan
näin:
v=[1 2 3]. Pystyvektorissa käytetään erottimena puolipistettä (tietysti, vrt. matriisi A yllä). Matriisikertolaskun merkki on * (Edellistä virkettä ei voi päättää pisteeseen!) - 6.
- Matriisin A transpoosi: A’ (reaalisessa tapauksessa).
- 7.
- Kokonaislukuvektori: Esim 1:10 tai 1:2:20. Myös linspace. Pystyvektoriksi transponoimalla.
- 8.
- A(i,j) A:n alkio (i,j).
A(2,:) A:n 2. rivi
A(:,3) A:n 3. sarake
A(1:4,1:4) osamatriisi
Matriisin osaa voi päivittää, vaikkapa:
A(1:4,1:4)=ones(4,4) tai
A(2,:)=A(2,:)-2*A(:,1) (Gaussin rivioperaatio). - 9.
- Matriisien liittäminen: Jos A:lla ja B:llä on yhtä monta riviä, ne voidaan
liittää peräkkäin: [A b]
(tai [A, b]). Jos yhtä monta saraketta, niin allekkain: [A;B] - 10.
- Laskutoimitukset tarkoittavat matriisilaskua. Siis esim.
A*B, A^p (jälkimmäinen mahdollinen vain neliömatriisille) - 11.
- Vektorien ja matriisien (samankokoisten) pisteittäinen eli alkioittainen
laskenta tapahtuu lisäämällä eteen piste. Esim: u=[1 2 3], v=[-2 -2
-2], u.*v.
Toinen operandi voi olla skalaari. Siten esim. vektorin u kaikki komponentit voidaan korottaa toiseen komennolla u.^2
(Ei siis tarvitse tehdä: u.^(2*ones(size(u))), joka tietysti toimii.) - 12.
- Piirtämistä varten muodostetaan x-vektori, joka edustaa diskretoitua
x-akselia ja lasketaan a.o. funktion arvo vektoriin y.
Piirto: plot(x,y);
Huom! Matlab-funktioita voi yleensä soveltaa vektoriin ja tulokseksi saadaan funktion arvojen muodostama vektori. Laskutoimitukset +,− operoivat vastinalkioittain (”pisteittäin”). Koska kerto- ja jakolasku sekä potenssiin korotus ^ on varattu matriisilaskutoimituksille, on ”pisteittäin” operoitaessa lisättävä piste (.) ao. laskutoimitusmerkin eteen. (+,−) merkkien eteen ei saa lisätä, ne ovat jo valmiiksi pisteittäisiä.)
Jos haluamme muodostaa vaikkapa funktion x2 arvot annetun x-vektorin pisteissä ja x-vektorina olkoon välin [-1,1] diskretointi 60:een osaan, voimme laskea ja piirtää näin:
x=linspace(-1,1,60); y=x.^2; plot(x,y) . Toinen tapa diskretoida on (:), esim: x=a:h:b;
jossa siis annetaan askeleen pituus h (askelten lukumäärän sijasta).Kts. help plot, help :, help colon
- 13.
- 3d-piirto: Pintojen ja korkeuskäyrien piirtämiseksi tarvitaan korkeusarvojen
matriisi xy-tason pistehilan päällä. Se aikaansaadaan helpoimmin (ja
rutiininomaisesti) meshgrid-komennolla. Jos haluaisimme piirtää vaikkapa
funktiopinnan f(x,y) = sin x cos y neliössä
![[− π,π ]](matlabHarPerusteet0x.png) ×
×![[− 2π,2 π]](matlabHarPerusteet1x.png) , ja hilapisteitä
olisi x-suunassa 25 ja y-suunnassa 50 kpl., tehtäisiin näin:
>> x=linspace(-pi,pi,25);
, ja hilapisteitä
olisi x-suunassa 25 ja y-suunnassa 50 kpl., tehtäisiin näin:
>> x=linspace(-pi,pi,25);
>> y=linspace(-2*pi,2*pi,50);
>> [X,Y]=meshgrid(x,y);
>> Z=sin(X).*cos(Y);
>> mesh(x,y,Z) % Rautalankakuva
>> surf(x,y,Z) % Kaunis pintakuva (myos surfl, surfc, colorbar,...)
>> contour(x,y,Z) % Korkeusk. piirros
Avainsanat: Matlab perusteet, harjoitus-pikaohje
- 2. mlP001a.tex
Olkoon z = [0 -1 2 4 -2 1 5 3], ja J = [5 2 1 6 3 8 4 7].
Mitä syntyy seuraavilla Matlab-komennoilla (sijoitetaan tilan säästämiseksi useita samalle riville.)x = z’, A = x*x’, s = x’*x, w = x*J,
length(x), length(z)
size(A), size(x), size(z), size(s)Vihje: Suorita doc length, doc size, tai etsi Matlabin Help index:n avulla (lisä)tietoa komennoista.
- 3. mlP002.tex
Muodosta vektori, joka koostuu parillisista kokonaisluvuista välillä![[21,66]](matlabHarPerusteet2x.png) .
.
- 4. mlP003.tex
Olkoon x=[2 5 1 6 7 4 3 2 1 11].- 1.
- Lisää jokaiseen alkioon luku 12
- 2.
- Lisää 3 parittomien indeksien osoittamiin alkioihin.
- 3.
- Laske vektorin alkioiden neliöjuuri.
- 4.
- Laske vektorin alkioiden neliöt ja neliösumma.
Vihje: Helppo tapa vektorin v indeksivektorin muodostamiseen:
ind = 1:length(v)
Miten siis parittomat indeksit?
Summaus sujuu helposti: help sum
Avainsanat: Matlab-alkeet, vektorien muodostus,vektorioperaatiot, indeksointi, kaksoispiste(:) .
- 5. mlP004.tex
Olkoon x = [3 2 6 8 0 -1]’ ja y=[4 1 3 5 0 0]’
- 1.
- Lisää vektorin x alkioiden summa vektoriin y
- 2.
- Korota vektorin x alkiot vektorin y vastinalkioiden osoittamiin potensseihin.
- 3.
- Jaa y:n jokainen alkio vektorin x vastinalkiolla.
- 4.
- Kerro x:n jokainen alkio y:n vastaavalla alkiolla ja talleta tulos muuttujaan z
Vihje: Tässä harjoitellaan aritmetiikkaa vektorilausekkeilla. Muista piste (.) laskuoperaation edessä (paitsi +,−). Summaukseen: help sum
Lue: help NaN ja help inf .
Huomaa: Matlab:lle 00 = 1 (eikä NaN) - 6. mlP005.tex
Muodosta vektori x, joka koostuu alkioista:- 1.
- 2, 4, 6, 8,…, 20
- 2.
- 10, 8, 6, 4, 2, 0,−2,−4,…,−10
- 3.
- 1, 1∕2, 1∕3, 1∕4, 1∕5,…, 1∕10
- 4.
- 0, 1∕2, 1∕3, 1∕4, 1∕5,…, 1∕10
Vihje: Kahdessa viimeisessä kohdassa voit selkeyttää komentamalla:
format rational
Paluu oletusformaattiin: format - 7. mlP006.tex
Määrittele vektoritx = [1 2 3 4 5]
y = [0 2 4 6]
z = [-4 -2 0 2 4 ]Kokeile seuraavia laskutoimituksia/komentoja:
x.*z
x*z’
x*z % Miksi virhe ?
x.^2 % Mika vektori?
x^2 % Miksi virhe ?
sqrt(x*x’)
sqrt(sum(x.^2)) % Miksi sama tulos kuin edella?
norm(x)
help normVihje:
- 8. mlP006a.tex
Muodosta vektori t, joka koostuu luvuista
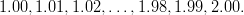
Vihje: help colon tai help :
Avainsanat Matlab-perusteet, vektorien muodostus, kaksoispiste,colon (:)
- 9. mlP007.tex
Määrittele matriisit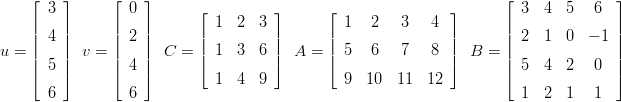 A*C C*A C^2 C.^2 A^2 A.^2
A*C C*A C^2 C.^2 A^2 A.^2Vihje: Tee skripti, jossa kukin laskutoimitus on omana %%-merkeillä erotettuna lohkonaan tyyliin:
%%
A*C % Lyhyt selitys
%%
C*A % Lyhyt selitys
%%
...Vie kursori kuhunkin lohkoon vuorollaan ja CTR-ENTER, ja seuraa Matlab-komentoikkunan tapahtumaa.
Avainsanat: Matlab perusteet, Matriisikertolasku, taulukko-operaatiot.
- 10. mlP008.tex
Edellisen tehtävän lyhennetty versio.
Määrittele matriisit
A =
 B =
B = 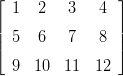 ,
,
Kokeile ja selitä:
A*B B*A A^2 A.^2 B^2 B.^2
Vihje: Tee skripti, jossa kukin laskutoimitus on omana %%-merkeillä erotettuna lohkonaan tyyliin:
%%
A*C % Lyhyt selitys
%%
C*A % Lyhyt selitys
%%
...Vie kursori kuhunkin lohkoon vuorollaan ja CTR-ENTER, ja seuraa Matlab-komentoikkunan tapahtumaa.
Avainsanat: Matlab perusteet, Matriisikertolasku, taulukko-operaatiot.
- 11. mlP009.tex
Vrt. opas:
http://math.tkk.fi/˜apiola/matlab/opas/mini/vektgraf.html#alkulukuskriptiAvaa uusi m-tiedosto (skripti) vaikkapa alkulukuja.m . Kirjoita siihen komennot, joilla saat selville kaikkien korkeintaan N:n suuruisten alkulukujen lukumäärän ja summan. Laske lisäksi lukumäärän suhde kaikken lukujen ≤ N lukumäärään, ja myös sama summille.
Aloita tiedosto näin:%% Selita, mita skripti tekee ja vaikka oma nimi, pvm. ym.
N = 100
alkuluvut= ...
lkm = ...
summa= ...
...
Apu: help primes (tai doc primes)
help sum .Myöhemmin: opitaan tekemään funktio-m-tiedostoja, jolloin N voidaan antaa parametrina omalle ”alkulukuja”-funktiolle.
Vihje:
Avainsanat: mlPerusteet, Matlab perusteet, skripti, m-tiedosto, alkuluvut, sum
- 12. mlP010.tex
- 1.
- Miten kääntäisit vektorin v alkiot vastakkaiseen järjestykseen kaksoispisteen (:) avulla?
- 2.
- Entä matriisin A sarakkeet, vastaavasti rivit?
Huom: Näihin on myös valmiit funktiot: fliplr, flipud ”LeftRight, UpDown” - 3.
- Miten limität (“merge”) kaksi samanpituista vektoria u ja v?
Tarkoitus on siis muodostaa vektori w =![[u1,v1,u2,v2,...]](matlabHarPerusteet7x.png)
Vihje: Liitä vektorit allekkain ja jonouta näin saatu 2-rivinen matriisi sarakkeittain (ovelaa). (Sarakkeittain jonoutus matriisille A saadaan näin: A(:).)
Avainsanat: mlPerusteet, Matlab perusteet, fliplr,flipud, kaksoispiste (:), käänteinen järjestys, kaanteinen jarjestys, matriisin jonoutus, “merge”, limitys
- 13. Matriisin kokoaminen osista, lohkomatriisit, skriptit
Nyt jo viimeistään on syytä ottaa skriptit käyttöön. Kts. skriptiohjetta (laitetaan myös tähän) (myös help script) (Itse asiassa skriptillä kannattaa aloittaa koko Matlab harrastus.)
Tutustu helpin avulla funktioihin: eye, ones, zeros, diag, size.
Aloita sitten hommat avaamalla uusi skripti-tiedosto, jonne kirjoitat kommentit ja komennot.Olkoot Y n×k ja Nn×k ykkösistä ja vastaavasti nollista koostuvia n × k-matriiseja ja olkoon In×n yksikkömatriisi. Muodosta seuraavat (lohko)-matriisit esim. arvoilla n = 4,k = 3. Rakenna skripti siten, että näitä on helppo muutella.
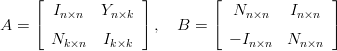
a) Poimi A :n pää- ja sivulävistäjä. Neuvo: Jälkimmäisessä on hyötyä vaikkapa fliplr-komennosta.
b) Poimi B:n “alalävistäjät”, jotka alkavat 4:n askeleen päässä päälävistäjästä 1. vaaka- ja 2. pystysuunnassa. (Edelleen: help diag).
Lopuksi voit käyttää publish-komentoa dokkarin aikaansaamiseksi. Totuttele tähän, ohjeita on ... (tähän viittauksia).
Avainsanat: mlPerusteet, matlabperusteet, Lohkomatriisit, skriptit, m-tiedostot, diag.
- 14. mlP012.tex
Taikaneliön saa komennolla magic(n) . Muodosta muutamalla pienehköllä n:n arvolla matriisin M=magic(n) rivisummat, sarakesummat, lävistäjäsumma ja sivulävistäjäsumma.Taikaneliöillä on mielenkiintoinen historia. Ne tunnettiin Kiinassa 2000 vuotta e.a.a.
http://www.mathworks.com/moler/intro.pdf Kts. Molerin kirjan introsta s. 18 alk. Myös Matlab:n dokumentaatiosta.Avainsanat: mlPerusteet, matlabperusteet, taikanelio, magic, rivisummat, sarakesummat,diag
- 15. mlP013.tex
Tässä vähän keskeneräistä muotoilua, mutta sopii “taikateemaan”. Tarkennellaan, kun ehditään ...Taikaneliöillä voisi demonstroida Markovin prosesseja, ehkä jätetään ominaisarvolaskujen yhteyteen. (vrt. http://math.tkk.fi/˜apiola/matlab/opas/lyhyt/tehtavia1.html teht. 6)
Tässä on joku, liittyy johonkin...
http://math.tkk.fi/opetus/v/matlab/opas/osa2.html#luku251Matlab-opas/elo/touko2010-sivuilla tarkempi tehtäväseloste.
Vihje:
Ratkaisu:
Avainsanat: Markovin matriisit, prosessit, ominaisarvot.
Liittyy: Lineaarialgebra/ominaisarvot. Aiemmissa kurssimatskuissa, myös Solmu-kirjoituksessa, koetehtävissä on monia tehtäviä ratkaisuineen.
- 16. mlP014.tex, mplP014.tex
Maple [Mathematica] , Matlab (erityisesti b)-kohta).
Tarkastellaan funktiota
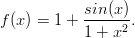
a) Maple: Määrittele f lausekkeeksi, laske f:n arvo pisteessä x = −2.0 ja piirrä kuvaaja välillä
![[− 5,5 ]](matlabHarPerusteet10x.png) .
.
Matlab:
Tee vastaava asia Matlabilla, kirjoita skripti. Huomaa, että Matlabissa täytyy ensin antaa x:lle numeerinen (vektori)arvo.b) Tee samat asiat, mutta nyt määrittelemällä f funktioksi.
Vihje:
a)
Maple Matlab:
> f:=1-... >> x=...
> subs... >> f=...
> plot >> plotb)
Maple Matlab
> f:=x->1-... >> f:=@(x) 1-...Ratkaisu: Ratkaisu:
mplPerusteet/mplP014R.mw ja .pdf
mlPerusteet/mlP014R.m ja .pdfLuokittelu:
mplteht/mplPerusteet/mplP014.tex, matlabteht/mlPerusteet/mlP014.tex
Avainsanat:
Mapleperusteet, funktiot, lausekkeet, Matlabperusteet
- 17. mlP015.tex
Kun Newtonin menetelmää sovelletaan yhtälöön x2 − a = 0, saadaan iteraatiojono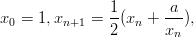
joka suppenee kohti lukua
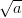 . Kirjoita MATLAB-skripti, jolla voit tarkastella tätä
suppenemista, kun a = 5.
. Kirjoita MATLAB-skripti, jolla voit tarkastella tätä
suppenemista, kun a = 5.
Anna tuloksena taulukko T, jossa on sarakkeet (vain numeeriset, ei otsikoita):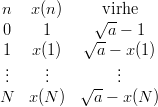
Vihje: Suppenemisen tutkimisessa voidaan käyttää for -luuppia. Se toimii syntaksilla
for k = 1:N-1
x(k+1)=...
virhe(k+1)=...
endOikean lopetusehdon muodostamiseen while-rakenne on parempi. Voitaisiin toteuttaa tähän tapaan:
a=...;
tol=10^(-6);
k=1;
suhtero=inf; % Ovela tapa aloitukseen.
x(1)=2;
while(suhtero>tol)
x(k+1)=(x(k)+a./x(k))/2;
k=k+1;
suhtero=abs(x(k)-x(k-1))/abs(x(k-1));
endTaulukon voit rakentaa vaikka liittämällä 3 pystyvektoria vierekkäin tai miksei suoraan for-luupissa. Edellinen tapa on ehkä selkeämpi. Kannattaa alustaa (pysty)vektorit x=ones(N,1); virhe=zeros(N,1); (Matlab ei sitä vaadi, mutta tehokkaampaa ja selkeämpää.) Numerointivektoria ei suotta ajeta luupissa, vaan ...
Tulostustarkkuuden säätö: format long (ei vaikuta laskentatarkkuuteen).
Huom: Indeksointi alkaa 1:stä Ratkaisu: http://math.aalto.fi/opetus/Mattie/MattieT/matlabteht/mlPerusteet/itersqrtscript.m
Funktioksi kirjoitettu, lisätty valinnaisten argumenttien käsittelyä:
http://math.aalto.fi/opetus/Mattie/MattieT/matlabteht/mlPerusteet/itersqrt.m Avainsanat: iteraatio, for, while, lopetusehto, Newtonin menetelmä neliöjuuren laskentaan. - 18. mlP016.tex
Avaa MatlabinFILE-valikosta uusi m-tiedosto ja valitse “skripti”. Talleta nimelle cossinplot.m.
Kirjoita/kopioi tiedostoon täällä oleva teksti
http://www.cs.cornell.edu/cv/Books/SCMV/Mfiles/chap1.htm#SinePlot
Voit kopioda sen myös tästä:%% Script File: SinePlot
% Displays increasingly smooth plots of sin(2*pi*x).
close all % Suljetaan mahd. avatut grafiikkaikkunat.
for n = [4 8 12 16 20 50 100 200 400]
x = linspace(0,1,n);
y = sin(2*pi*x);
plot(x,y)
title(sprintf(’Plot of sin(2*pi*x) based upon n = %3.0f points.’,n))
pause(1)
endSuorita komennot
- copy/paste:lla istuntoon tai
- editorin vihreällä nuolella tai F5:llä tai CTR-ENTER tai
- kirjoittamalla Matlab-istuntoon tiedoston nimi: cossinplot
Muuta pause-komento muotoon pause(), jolloin komentojono jää odottamaan ENTER-painallusta. Voit kirjoittaa ennen pause- komentoa kehoituksen tyyliin disp(’Paina ENTER:iä jatkaaksesi’). Samalla voit editoida n-vektoria loppupäästä lyhyemmäksi.
Näin pääset hallitummin katsomaan tilannetta.
Ratkaisu: Ei tarvita.
Avainsanat: Skripti, komentotiedosto, kuva, piirto
- 19. mlP017.tex
Vahvista numeerisesti uskoasi matemaattiseen totuuten siitä, että summa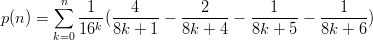
suppenee kohti arvoa π kun n →∞. Vihje: a) Käytä for-luuppia, jossa kasvatat iteraatioiden ylärajaa suureksi. Suppeneminen on suhteellisen nopeaa, joten ylärajan ei tarvitse olla kovin iso.
b) Voit suoritta tehtävän myös (ja mieluiten) vektoroidusti muodostamalla jonot kaksoispiste (:) - operaattorilla, aritmetiikan pisteittäin (.) ja soveltamalla sum-funktiota tai vielä paremmin cumsum:ia, jolla saat koko osasummien jonon.
Kirjoita skriptiksi, jossa voit vaihdella parametria n, tottakai!
- 20. mlP018.tex
Huom: Tehtävä on varsin tarkkaan neuvottu. Pituus ei merkitse vaikeutta.
Tutkitaan heitetyn pallon lentorataa MATLABilla. Aloita luomalla m-tiedosto johon kirjoitat tarvittavat komennot.
- 1.
- Teemme seuraavat lähtöoletukset:
- i
- Pallon korkeus h heittohetkellä on 1.5m
- ii
- Putoamiskiihtyvyys g on 9.8m∕s2
- iii
- Pallon vauhti v heittohetkellä on 4m∕s
- iv
- Pallon etenemisvektorin suunta 𝜃 on 45o
Kirjoita oletukset skriptiisi.
- 2.
- Luo vektori t, jossa on 1000 tasaisin välein valittua arvoa väliltä [0, 1].
- 3.
- Kuvataan muuttujalla x pallon etäisyyttä heittäjästä (mitattuna maan
pinnalla) ja muuttujalla y pallon korkeutta, seuraavat yhtälöt kuvaavat
muuttujien riippuvuutta ajasta ja oletetuista parametreista.
- (a)
-

- (b)
-
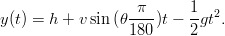
Kirjoita annettujen yhtälöiden ja määrittelemiesi arvojen avulla vektorit x ja y.
- 4.
- Arvioidaan hetkeä jolloin pallo putoaa maahan, ja sen lentämää matkaa: etsi ensimmäinen indeksi, jolla pallon korkeus y muuttuu negatiiviseksi (käytä funktiota find). Pallon lentämä etäisyys on vektorin x arvo tässä indeksissä, lentoaika on vektorin t arvo tässä indeksissä. Tulosta sekä lentomatka että -aika näkyviin ruudulle.
- 5.
- Piirretään pallon lentorata: piirrä kuva, jossa pisteiden x-koordinaatit ovat vektorissa x, ja y-koordinaatit vektorissa y. Tämän jälkeen piirrä nolla-taso näkyviin katkoviivalla.
- 21. mlP019.tex
Olkoon
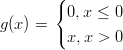
Määrittele funktio g Matlab-funktioksi (m-tiedostoon).
Vihje: Voit käyttää funktioita zeros ja max .
Ehkä vieläkin elegantimmin näin:
Mieti, millä saat aikaan yksikköaskelfunktion (Heavisiden funktion), joka saa negatiivisilla arvon 0 ja positiivisilla 1. (Tähän riittää 3 merkkiä.) Sillä kerrot funktion y = x.Ratkaisu: mlP019R.m ja .pdf
Avainsanat: Matlabperusteet, signaalinkasittely, ramppifunktio, Heavisiden funktio, paloittain maarittely, zeros, x>0 : elegantti.
- 22. mlP020.tex
(Maple ja Matlab)Määritä seuraavat summat:
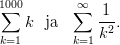
Vihje: Maple: Kokeile edelliseen sekä sum että add - komentoja, jälkimmäiseen vain sum.
Matlab: Muodosta vektori 1,2,…1000 ja sitten vain sum. Jälkimmäisessä voit laskea muutamalla, toinen toistaan suuremmalla arvolla. (Numeerisesti et tietenkään voi summata äärettömyyksiin.)
- 23. mlP021.tex
Esitä yhden rivin Matlab-komento, jolla saat selville vektorin tai matriisin niiden alkioiden lukumäärän, jotka ovat > 5.
Testaa ainakin näille:
a) A=1:10
b) B=[1 2 3;4 5 6;7 8 9]
c) C=10*rand(6,6)
d) D=ones(4,4)
