| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Mathematica harjoitustehtäviä liittyen yhtälöiden ratkaisemiseen Mathematicassa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se Mathematica-pääsivulta löytyvään harjoituspohjaan.
- 1. Etsi yhtälön x3 − 2x − 5 = 0 kaikki juuret. Etsi sekä tarkat arvot että likiarvot ja sijoita kummatkin takaisin yhtälöön. Toteutuuko yhtälö? Vihje: Likiarvot voidaan laskea joko tarkkojen arvojen likiarvoina funktiolla N tai suoraan käyttämällä funktiota NSolve. Juurten sijoittaminen yhtälöön: yhtalo/.korvaus, missä /. on lyhennemerkintä Mathematican funktiolle ReplaceAll.
- 2. Etsi yhtälön x7 − 2x − 5 = 0 kaikki juuret. Sijoita jonkin juuren kaksi-, kolmi- ja nelidesimaaliset likiarvot alkuperäiseen yhtälöön ja tutki, millä tarkkuudella se toteutuu. Onko juurille mahdollista löytää tarkat arvot? Kuinka monta reaalista juurta yhtälöllä on? Voidaanko yhtälön toteutumisen tarkkuudesta päätellä juuren likiarvon tarkkuus? Vihje: Mathematican versiosta riippuen juurten tarkat arvot saatetaan esittää hieman erikoisessa muodossa Root-funktion avulla. Tämä itse asiassa ilmoittaa vain, että kyseessä on juuri tämän polynomin juuri!
- 3. Muodosta toisen asteen yhtälön yleiset ratkaisukaavat ratkaisemalla yhtälö ax2 + bx + c = 0. Laske x 12 + x 1x2 + x22, missä x 1 ja x2 ovat saadut juuret. Tarkastele esimerkkinä yhtälöä 2x2 + 3x + 4 = 0. Vihje: Suorita laskut siten, että et joudu käsin syöttämään uudelleen jo laskettuja tuloksia. Käytä korvausoperaattoria ReplaceAll eli /. sopivalla tavalla. Esimerkkiyhtälön juuret ovat kompleksilukuja, mutta juurista muodostettu lauseke on yksinkertainen reaalinen murtoluku.
- 4. Johda Solve-funktiota käyttäen toisen ja kolmannen asteen yhtälön yleiset ratkaisukaavat. Ratkaise näiden avulla yhtälöt 15x2 + 2x + 12 = 0 ja x3 − 2x − 5 = 0 sijoittamalla kertoimien arvot ratkaisukaavaan. Syntyykö toisen asteen tapauksessa tutut ratkaisukaavat? Antaako kertoimien sijoittaminen ratkaisukaavaan samat juuret kuin yhtälön ratkaiseminen suoraan? Vihje: Yleiset ratkaisukaavat saadaan ratkaisemalla Solve-funktiolla yhtälöt, joissa kertoimet ovat symboleja.
- 5. Ratkaise yhtälö x3 + 1 = 0 sijoittamalla kertoimien arvot kolmannen asteen yhtälön yleiseen ratkaisukaavaan. Antaako kertoimien sijoittaminen ratkaisukaavaan samat juuret kuin yhtälön ratkaiseminen suoraan? Vihje: Kolmannen asteen yhtälön yleinen ratkaisukaava on sangen mutkikas eikä kaikissa tapauksissa anna ongelmitta oikeaa ratkaisua. Ratkaistaessa yhtälö suoraan saatetaan tarvita funktiota ComplexExpand saatujen juurten sieventämiseen.
- 6. Etsi yhtälön x4 − 2x3 + 2x2 − 6x − 3 = 0 juuret. Jaa yhtälön vasempana puolena oleva polynomi näiden avulla mahdollisimman alhaista astetta oleviin reaalisiin tekijöihin. Onko tulos sama kuin Factor-funktion antama? Vihje: Solve-funktion antamasta korvauslistasta voidaan poimia k:s korvaussääntö joko hiiren avulla tai asettamalla listan nimen perään indeksi kaksinkertaisiin hakasulkuihin, esimerkiksi ratk[[k]]. Tulos voidaan saada myös Factor-funktiolla, mutta siinä tarvitaan lisäoptio; ks. Mathematican dokumentaatiota.
- 7. Ratkaise yhtälö z7 + 1 = 0. Esitä juuret muodossa z = x + iy ja tutki, miten kaukana origosta juuret sijaitsevat kompleksitasossa. Mitkä ovat juurten napakulmat? Vihje: Sievennä juurten lausekkeet ComplexExpand-funktiolla. Kompleksiluvun itseisarvo saadaan funktiolla Abs, napakulmaan voidaan käyttää funktiota Arg (vaikka tulos kyllä näkyy muutenkin).
- 8. Ratkaise kompleksinen yhtälö z3 − iz2 + 2iz + (8 − 4i) = 0. Vihje: Imaginaariyksikkö on I. Se voidaan myös valita paletista, jolloin symboli on hieman erinäköinen.
- 9. Tutki eri tapoja ratkaista itseisarvoyhtälö |x − 1| + |x − 3| = 3 Mathematicalla. Vihje: Itseisarvofunktio on Abs. Yhtälöön voidaan suoraan soveltaa yhtälöiden ratkaisemisessa käytettäviä komentoja itseisarvolausekkeita ensin purkamatta. Piirrä myös kuvio (Plot).
- 10. Ratkaise yhtälö |3x + 1| + |2x − 3| = ax + |5x − 7| käyttäen funktiota Solve; a on jokin reaalinen vakio. Kokeile, toteuttavatko saadut juuret yhtälön. Vihje: Voi olla hyödyksi tutkia yhtälön toteutumista antamalla a:lle sopivia arvoja. Itseisarvofunktio on Abs.
- 11. Ratkaise lineaarinen yhtälöryhmä
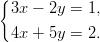
Vihje: Solve-funktion ensimmäisenä argumenttina voi olla usean yhtälön muodostama lista ja toisena usean tuntemattoman muodostama lista.
- 12. Ratkaise yhtälöryhmät
a)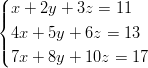
b)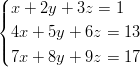
c)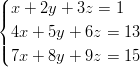
Montako ratkaisua yhtälöryhmillä on? Vihje: Ryhmän rakennetta voi myös tutkia tarkemmin eliminoimalla esimerkiksi tuntemattoman x kahdesta ensimmäisestä ja vastaavasti kahdesta jälkimmäisestä yhtälöstä. Tällöin on apua Mathematican funktiosta Eliminate. - 13. Ratkaise yhtälöpari
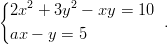
Millä vakion a arvoilla yhtälöparilla on reaalisia ratkaisuja? Vihje: Ratkaise ensin yhtälöpari ja poimi hiirellä ratkaisusta ehto luvulle a. Epäyhtälöitä voidaan ratkaista funktiolla Reduce.
- 14. Ratkaise käyrien
leikkauspisteiden koordinaatit. Vertaa tulosta käyrien kuvaajiin. Vihje: Kumpi on järkevämpää: Hakea leikkauspisteiden koordinaateille tarkat arvot vai likiarvot? Kuvaajat voidaan piirtää funktiolla ContourPlot.16x2 + 9y2 + 24xy − 170x + 310y − 465 = 0 ja 5x2 + 8y2 + 4xy − 32x − 56y + 80 = 0. - 15. Ratkaise yhtälö ln(x2 + 1) =
.
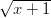Vihje: Piirrä kuvio (Plot) ja selvitä sen avulla yhtälön juurten lukumäärä. Voidaanko juurille
löytää tarkat arvot? Mitä yhtälönratkaisufunktioista Solve, NSolve, FindRoot voidaan
käyttää? Miksi? Luonnollinen logaritmi on Log.
- 16. Ratkaise yhtälö e−x − sin x = 0. Piirrä tätä varten funktioiden y = e−x ja y = sin x kuvaajat samaan kuvioon. Määritä kolmen pienimmän juuren likiarvot. Montako juurta yhtälöllä on? Mitä voidaan sanoa näiden ratkaisemisesta a) algebrallisesti, b) numeerisesti? Vihje: Funktiota Solve tai edes NSolve ei voida käyttää, koska kyseessä on transkendenttiyhtälö. Iteratiiviseen numeeriseen ratkaisemiseen (Newtonin menetelmän tapaan) on käytettävissä funktio FindRoot.
- 17. Etsi yhtälöparin ex + sin y = 0, x6 − xy + y6 = 4 juuret numeerisesti. Vihje: Funktioita Solve ja NSolve ei voida käyttää, koska ne ratkaisevat vain algebrallisia yhtälöitä. Transkendenttinen yhtälö tai yhtälöryhmä voidaan ratkaista funktiolla FindRoot, joka oleellisesti käyttää yksi- tai useampiulotteista Newtonin menetelmää. Sopivien alkuarvojen löytämiseksi käyrät on syytä piirtää. Tällöin voidaan käyttää funktiota ContourPlot.
- 18. Osa tien kaarteesta on ympyrän kaari, joka kartalla kulkee xy”=koordinaatiston pisteiden (28, 98), (70, 112) ja (126, 84) kautta. Kuinka suuri on tämän ympyrän säde, kun yksikkö kartalla vastaa 25:tä metriä luonnossa? Vihje: Ratkaise kolmen algebrallisen yhtälön ryhmä. Muodosta tätä varten ensin ympyrän yhtälö, jossa säde ja keskipisteen koordinaatit ovat tuntemattomia, ja sijoita siihen annetut arvot.
- 19. Määritä ympyröiden x2 + y2 − 4x − 6y + 10 = 0 ja x2 + y2 + 2x − 2y − 3 = 0 leikkauspisteet, laske niiden etäisyydet origosta ja niiden keskinäinen etäisyys. Vihje: Käytä Solve-komennon tuottamia korvaussääntöjä mahdollisimman tehokkaasti. Etäisyydet voi ehkä helpoimmin laskea vektoreiden pituuksina.
- 20. Kolmen pallon keskipisteet ja säteet ovat (1, 1, 1), 3; (1, 2, 3), 2; (3, 2, 4), 4. Määritä pallojen yhteiset pisteet. Vihje: Käytä funktiota Solve usean algebrallisen yhtälön muodostaman ryhmän ratkaisemiseen.
- 21. Kolmannen asteen polynomilla p(x) on kaksinkertainen nollakohta x = 2 ja p(3) = 15, p′(1) = 0. Määritä p(x). Vihje: Muodosta polynomille lauseke tuntemattomin kertoimin ja johda kertoimille yhtälöryhmä ehtojen perusteella.
- 22. Määritä vakio a siten, että yhtälön x4 − ax2 + 2x + 1 = 0 juurten neliöiden summa on 1. Mitkä ovat vastaavien juurten likiarvot? Vihje: a on yksinkertainen murtoluku; kaksi juurista on kompleksisia. Tehtävän voi laskea monella tavalla. Tutki, mitä antavat seuraavantyyppiset syötteet: neliot= x^2/.Solve[...], Apply[Plus,neliot].