
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Mathematica harjoitustehtäviä liittyen vektorianalyysiin.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se Mathematica-pääsivulta löytyvään harjoituspohjaan.
- 1. Jaa vektori c = 7i + 5j vektoreiden a = 3i + 4j ja b = 5i − j suuntaisiin komponentteihin. Vihje: Esitä vektorit kaksialkioisina listoina. Muodosta näiden avulla vektoriyhtälö ja ratkaise se Solve-funktiolla.
- 2. Olkoot A = (7, 3), B = (1, 2) ja C = (3, 5) tason pisteitä. Muodosta kulman ABC puolittajan suuntavektori ja sen suuntainen yksikkövektori. Vihje: Syötä aluksi pisteet kahden alkion listoina ja muodosta näiden avulla tarvittavat vektorit. Puolittajavektori saadaan helpoimmin kulman kylkien suuntaisten yksikkövektoreiden summana.
- 3. Kolmion kärkipisteet ovat (1, 2), (−3, 5) ja (−1,−6). Määritä kolmion keskijanojen leikkauspiste (x,y) muodostamalla sille vektoriyhtälöt ja ratkaisemalla koordinaatit näistä. Osoita laskemalla, että keskijanat todellakin leikkaavat samassa pisteessä, joka jakaa keskijanat suhteessa 1 : 2. Vihje: Solve-komennolla voidaan ratkaista myös vektoriyhtälöiden muodostama ryhmä. Vaadi esimerkiksi, että pisteen (x,y) ja kolmion kärkipisteen yhdysvektori on samasta kärjestä vastakkaisen sivun keskipisteeseen suuntautuvan vektorin skalaarikerrannainen. Koska kärkiä on kolme, saadaan kolme vektori- eli kuusi skalaariyhtälöä, joissa on viisi tuntematonta: x, y ja kolme skalaarikerrointa.
- 4. Todista yleisesti, että kolmion keskijanat leikkaavat toisensa samassa pisteessä, joka jakaa ne suhteessa 1 : 2. Tarkastele tätä varten kolmiota, jonka kärkipisteet ovat (a1,a2), (b1,b2) ja (c1,c2). Merkitse keskijanojen leikkauspistettä (x,y) ja muodostama sille vektoriyhtälöt. Ratkaise nämä ja tulkitse tulos. Vihje: Solve-komennolla voidaan ratkaista myös vektoriyhtälöiden muodostama ryhmä. Vaadi esimerkiksi, että pisteen (x,y) ja kolmion kärkipisteen yhdysvektori on samasta kärjestä vastakkaisen sivun keskipisteeseen suuntautuvan vektorin skalaarikerrannainen. Koska kärkiä on kolme, saadaan kolme vektori- eli kuusi skalaariyhtälöä, joissa on viisi tuntematonta: x, y ja kolme skalaarikerrointa.
- 5. Vektorit a, b ja c ovat kolmion kärkipisteiden A, B ja C paikkavektorit. Olkoon P sivuille AC ja BC piirrettyjen korkeusjanojen leikkauspiste ja p sen paikkavektori. Tällöin pätee

Jos voidaan todistaa, että myös (p − c) ⋅ (a − b) = 0, on tullut todistetuksi, että kaikki kolme korkeusjanaa leikkaavat samassa pisteessä. Suorita todistus Mathematican vektorialgebraa käyttäen. Vihje: Esitä tehtävän vektorit symbolisina kaksi- (tai kolmi-) komponenttisina listoina, so. Mathematican vektoreina. Funktioista Simplify ja FullSimplify on apua; katso dokumentaatiota.
- 6. Kolmiulotteisen avaruuden taso kulkee pisteiden A = (7, 3, 1), B = (1, 2, 3) ja C = (3, 5,−5) kautta. Laske tason yksikkönormaalivektori. Vihje: Syötä pisteet kolmialkioisina listoina ja laske näillä. Normaali voidaan määrittää joko skalaaritulojen avulla tai vektorituloa käyttäen.
- 7. Määritä u siten, että vektoreiden i + 2j + 3k ja ui + 5j + 6k välinen kulma on 60 astetta. Vihje: Hyödynnä skalaarituloa. Mieti, montako ratkaisua tehtävällä on. Tarkista saamasi tulos.
- 8. Kolmiulotteisessa avaruudessa sijaitsevan kolmion kärkipisteet ovat (1, 2, 3), (−2, 4, 5) ja (2,−5,−7). Laske kolmion ala. Vihje: Käytä vektoreita. Kolmion ala voidaan lausua ristitulon (Cross) avulla.
- 9. Kolmiulotteisessa avaruudessa sijaitsevan kolmion kärkipisteet ovat (1, 2, 3), (−2, 4, 5) ja (2,−5,−7). Laske kolmion kulmien suuruudet asteissa. Vihje: Sovella vektorialgebraa, erityisesti skalaarituloa. Kosinifunktion käänteisfunktio on ArcCos; tämä antaa kulman suuruuden radiaaneina.
- 10. Mikä suoran (x,y) = (1, 2) + t(3, 4) piste on lähinnä pistettä (8, 1)? Mikä on tämä lyhin etäisyys? Vihje: Käytä vektorialgebraa.
- 11. Mikä suoran (x,y,z) = (3, 0, 1) + t(1, 1, 4) piste on lähinnä pistettä (1, 4, 2)? Mikä on tämä lyhin etäisyys? Vihje: Käytä vektorialgebraa.
- 12. Missä pisteessä suora (x,y,z) = (1, 2, 3) + t(4, 5, 6) leikkaa tason x − 2y + 3z − 4 = 0? Vihje: Käytä vektorialgebraa.
- 13. Taso kulkee pisteiden (1, 2, 3), (−2, 4, 5) ja (2,−5,−7) kautta. Mikä tason piste on lähinnä pistettä (3, 2, 1) ja mikä on tämä lyhin etäisyys? Vihje: Käytä vektorialgebraa.
- 14. Tarkastellaan avaruuskäyrää r(t) = eti + e−tj +
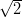 tk, t ∈ ℝ. Piirrä käyrä.
tk, t ∈ ℝ. Piirrä käyrä.
a) Muodosta käyrälle parametriesitys, missä parametrina on arvoa t = 0 vastaavasta pisteestä parametrin t kasvusuuntaan mitattu kaarenpituus s.
b) Määritä käyrältä piste P, joka on käyrää pitkin mitattuna etäisyydellä 2 pisteestä (1, 1, 0) parametrin t kasvusuuntaan. Laske koordinaattien likiarvot ja vertaa kuvaan.
c) Laske käyrän kaarevuus ja kierevyys pisteessä P sekä tähän pisteeseen liittyvä kolmikanta {t,n,b}.
d) Määritä käyrän pisteeseen P liittyvän kaarevuusympyrän keskipiste ja säde.
e) Missä pisteessä käyrän kaarevuus on suurimmillaan ja mikä on maksimiarvo? Vastaavatko arvot kuvaa?
f) Missä pisteessä käyrän kierevyys on suurimmillaan ja mikä on maksimiarvo?
Vihje: Kertaa käyräteoria jostakin oppikirjasta! Em. laskujen läpivieminen johtaa yleensä vaikeuksiin, koska kaarenpituusintegraalista tulee liian monimutkainen. Tehtävän käyrä on kuitenkin poikkeuksellinen: lasku onnistuu! Syötä käyrä Mathematican vektorina, so. kolmialkioisena listana ja laske vektorialgebraa käyttäen. - 15. Muodosta lista (vektori), jossa on 20 ensimmäistä alkulukua. Muodosta toinen lista, jossa on 20 ensimmäistä sellaista alkulukua, joiden järjestysluku on myös alkuluku. Vihje: Tarvittavia funktioita: Table, Prime. Kiinnostava voi olla myös PrimeQ
- 16. Määrätty integraali voidaan laskea numeerisesti esimerkiksi puolisuunnikassäännöllä
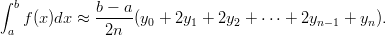
Tässä integroimisväli on jaettu n yhtä suureen osaväliin ja luvut yk tarkoittavat funktion arvoja jakopisteissä. Laske integraali ∫ 01e−x2dx puolisuunnikassäännöllä käyttäen arvoja n = 4, 8, 12, 16, 20. Muodosta jokaisessa tapauksessa ensin kaksi vektoria: toisessa on funktion arvot tarvittavissa jakopisteissä ja toisessa vastaavat painokertoimet. Vihje: Anna aluksi arvo muuttujalle n ja muodosta vektorit tämän avulla. Miten vektoreiden sisätuloa voidaan laskennassa hyödyntää? Miten tulokset saadaan helpoimmin muilla arvoilla n? Miten nämä suhtautuvat NIntegrate-funktion antamaan tulokseen?
- 17. Määrätty integraali voidaan laskea numeerisesti esimerkiksi Simpsonin säännöllä
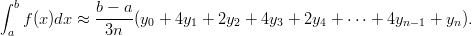
Tässä integroimisväli on jaettu parilliseen määrään n yhtä suuria osavälejä ja luvut yk tarkoittavat funktion arvoja jakopisteissä. Laske integraali ∫ 01e−x2dx Simpsonin säännöllä käyttäen arvoja n = 4, 8, 12, 16. Muodosta jokaisessa tapauksessa ensin kaksi vektoria: toisessa on funktion arvot tarvittavissa jakopisteissä ja toisessa vastaavat painokertoimet. Vihje: Anna aluksi arvo muuttujalle n ja muodosta vektorit tämän avulla. Painokerroinvektoria muodostettaessa voidaan käyttää esimerkiksi Mathematican funktioita If ja EvenQ (katso dokumentaatiota). Miten vektoreiden sisätuloa voidaan laskennassa hyödyntää? Miten tulokset saadaan helpoimmin muilla arvoilla n? Miten nämä suhtautuvat NIntegrate-funktion antamaan tulokseen?
