
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Mathematica harjoitustehtäviä liittyen lausekkeiden kanssa toimimiseen Mathematicassa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se Mathematica-pääsivulta löytyvään harjoituspohjaan.
- 1. Sievennä lauseke
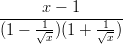 .
Vihje: Sopivia Mathematican funktioita ovat Simplify ja FullSimplify.
.
Vihje: Sopivia Mathematican funktioita ovat Simplify ja FullSimplify.
- 2. Talleta lauseke (a + b)10 jollekin nimelle ja kehitä se. Jaa tulos tekijöihin, jolloin palataan alkuperäiseen lausekkeeseen. Vihje: Tarvittavat Mathematican funktiot ovat Expand ja Factor. Näiden argumenttina oleva lauseke voi olla joko hakasuluissa tai komento voidaan kirjoittaa sen perään: Expand[lauseke] tai lauseke//Expand.
- 3. Jaa tekijöihin kahden muuttujan polynomi
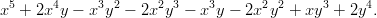
Kehitä saamasi tulos, jolloin palataan alkuperäiseen lausekkeeseen. Vihje: Tarvittavat Mathematican funktiot ovat Expand ja Factor.
- 4. Tutki, mikä lauseke on tekijänä lausekkeessa an − bn riippumatta eksponentin n ∈ ℕ arvosta. Missä tapauksessa lausekkeella an + bn on vastaavanlainen tekijä? Supista lausekkeet
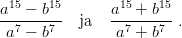
Mitä säännönmukaisuutta tuloksen osoittajassa ja nimittäjässä on? Vihje: Tekijöihin jako: Factor. Supistaminen: Cancel. Kokeile luvulle n erikseen eri arvoja. (Miksi yleistä symbolia n ei voida käyttää?) Kokeilut voidaan laskea myös yhteen taulukkoon käyttämällä komentoa Table; tulostuksen saa hieman selkeämpään muotoon kirjoittamalla komennon jälkeen //TableForm.
- 5. Lavenna murtolauseke
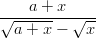
siten, että juuria ei esiinny nimittäjässä. Vihje: Murtolausekkeesta voi poimia osoittajan funktiolla Numerator ja nimittäjän lausekkeella Denominator. Kokeile myös, mitä tapahtuu, kun murtolausekkeeseen kohdistetaan peräkkäin funktiot Apart ja Simplify. Mitä nämä periaatteessa tekevät?
- 6. Hajota seuraavat rationaalilausekket osamurtokehitelmiksi, joissa nimittäjät ovat ensimmäistä astetta tai ensimmäisen asteen polynomin potensseja:
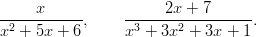
Miten päästään takaisin alkuperäiseen lausekkeeseen? Vihje: Sopivia funktioita: Apart, Together, Simplify, Expand ...
- 7. Muodosta osamurtokehitelmä lausekkeelle
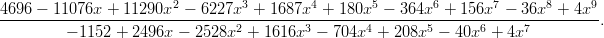
Lisää tämän jälkeen lausekkeen nimittäjään 1 ja muodosta osamurtokehitelmä uudelleen. Miksi toisessa tapauksessa onnistutaan, toisessa ei? Vihje: Sopivia funktioita: Apart, Numerator, Denominator. Myös hiirtä ja paletteja voi hyödyntää.
- 8. Tutki, tarkoittaako Mathematican merkintä x^x^x samaa kuin (x^x)^x vai samaa kuin x^(x^x). Sievennä, derivoi ja integroi kumpikin vaihtoehto. Vihje: Yksinkertainen sievennyskomento Simplify ei auta, koska Mathematica varautuu mahdollisuuteen, että muuttujat ovat kompleksisia, jolloin tavanomaiset laskusäännöt eivät rajoituksitta olekaan voimassa. Kokeile tämän johdosta seuraavia sievennyskäskyjä: Simplify[..., x>0] ja PowerExpand. Katso näiden komentojen tarkempaa selitystä Mathematican dokumentaatiosta.
- 9. Talleta lauseke
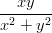 jollekin nimelle ja laske sen arvo, kun a) x = 2, y = 3, b) x = −5,
y = π. Laske sekä tarkka arvo, että 50-desimaalinen likiarvo. Ovatko desimaaliesitykset
jaksollisia?
Vihje: Käytä arvojen sijoittamisessa korvausoperaattoria /. (eli ReplaceAll). Likiarvojen
laskeminen funktiolla N.
jollekin nimelle ja laske sen arvo, kun a) x = 2, y = 3, b) x = −5,
y = π. Laske sekä tarkka arvo, että 50-desimaalinen likiarvo. Ovatko desimaaliesitykset
jaksollisia?
Vihje: Käytä arvojen sijoittamisessa korvausoperaattoria /. (eli ReplaceAll). Likiarvojen
laskeminen funktiolla N.
- 10. Mathematicassa on kaksi operaattoria, joilla muuttujalle annetaan arvo: joko = (eli Set) tai := (eli SetDelayed). Yritä selvittää näiden ero antamalla syötteeta=RandomInteger[–1,100˝]
Table[a,–10˝]
b:=RandomInteger[–1,100˝]
Table[b,–10˝]Vihje: Delay = viivästää. Katso myös Mathematican dokumentaatiota. Funktio RandomInteger generoi satunnaisia kokonaislukuja; sen argumenttina annetaan väli, jolta luvut otetaan.
- 11. Kaksi matkapuhelinmastoa näkyy paikkaan, jonka etäisyys toisesta mastosta on 5,27 km ja toisesta 3,16 km. Tähtäyssuunnat mastoihin muodostavat 72∘50′ suuruisen kulman. Kuinka etäällä mastot ovat toisistaan? Etäisyydet mitataan vaakasuorasti, eikä maaston mahdollisia korkeuseroja oteta huomioon. Vihje: Trigonometristen funktioiden argumentit ilmoitetaan Mathematicassa radiaaneissa. Radiaanien ja asteiden välinen muunnoskerroin on valmiina nimellä Degree (katso dokumentaatiota), mutta kertoimen voi tietenkin muodostaa itsekin. Muista: Funktioiden nimet kirjoitetaan isolla alkukirjaimella, argumentit annetaan hakasuluissa.
- 12. Tutki lausekkeiden
- a)
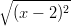
- b)
- sin(5x)
- c)
- sin(x + y)
- d)
- exp(ix) + exp(−ix)
- e)
- cos(arccos x)
- f)
- arccos(cos x)
- g)
- exp(ln x)
- h)
- ln(exp x)
sieventämistä. Mitä näistä pitäisi tulla? Mitä Mathematica antaa ja millä komennolla? Mitä symbolisen ohjelman itse asiassa pitäisi antaa vastaukseksi, kun muuttujaa x ei ole millään tavoin rajoitettu? Vihje: Mathematicalla on useita erilaisia Expand- ja Simplify-tyyppisiä komentoja. Muista: Funktioiden nimet kirjoitetaan isolla alkukirjaimella, joskus isoja kirjaimia voi olla muuallakin: ArcCos. Argumentit annetaan hakasuluissa. Imaginaariyksikkö on I.
- 13. Muokkaa muotoa sin(nx), cos(nx), sin nx, cos nx olevia trigonometrisia lausekkeita erilaisiin muotoihin, kun n on jokin luonnollinen luku (ei symboli). Vihje: Käytä funktioita TrigFactor, TrigExpand, TrigReduce, ExpToTrig, TrigToExp. Muista: Funktioiden nimet kirjoitetaan isolla alkukirjaimella, argumentit annetaan hakasuluissa.
- 14. Sievennä Tšebyševin polynomin lauseke Tn(x) = cos(n arccos x), n ∈ ℕ, muotoon, josta ilmenee, millainen polynomi on kyseessä. Mikä on polynomin asteluku? Vihje: Anna symbolille n numeerisia arvoja. Funktioiden nimet ovat Cos ja ArcCos.
- 15. Astetta n olevan polynomin nollakohdat olkoot x1,x2,…,xn. Määritä polynomien kertoimien lausekkeet nollakohtien funktioina tapauksissa n = 2, 3, 4, 5. Miten polynomin kertoimet riippuvat nollakohdista? Vihje: Polynomi voidaan nollakohtien avulla kirjoittaa tulomuotoon
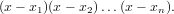
Hyödyllisiä funktioita ovat mm. Product, Collect, Coefficient, CoefficientList. Jos listassa on pitkiä alkioita, sen voi tulostaa selkeämpään muotoon kirjoittamalla perään //TableForm.
- 16. Yhtälöt
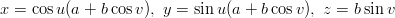
esittävät erästä pintaa, ympyrärengasta eli torusta parametrimuodossa. Etsi torukselle muotoa F(x,y,z) = 0 oleva yhtälö eliminoimalla eo. yhtälöistä parametrit u ja v. Vihje: Eliminointi voidaan tehdä funktiolla Eliminate; ks. käyttöohjeet Mathematican dokumentaatiosta. Se toimii kuitenkin parhaiten polynomeihin sovellettuna ja trigonometristen funktioiden tapauksessa ei kovin yksinkertaisiin lausekkeisiin päästä. Vaikeudet voidaan välttää seuraavasti: Eliminoitaviksi muuttujiksi otetaan parametrien u ja v sijasta niiden sinit ja kosinit, ts. tehdään eo. yhtälöihin sijoitus Sin[u]->u1, Cos[u]->u2, Sin[v]->v1, Cos[v]->v2. Uusien muuttujien välillä ovat voimassa yhtälöt u1^2 + u2^2 == 1 ja v1^2 + v2^2 == 1, jolloin on kaikkiaan viisi yhtälöä, joista on eliminoitava neljä muuttujaa.
- 17. Yhtälö
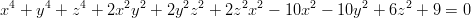
esittää erästä kolmiulotteisen avaruuden pintaa, ympyrärengasta eli torusta. Jos pintaa leikataan tasolla z = 0 tai tasolla x = 0, saadaan leikkauskäyräksi kaksi ympyrää. Määritä näiden yhtälöt. Vihje: Muodosta leikkauskäyrien yhtälöt sijoittamalla vuorollaan arvot x = 0 ja z = 0 annettuun yhtälöön. Jaa yhtälön vasen puoli tekijöihin! (Mahdollista tarvetta varten: Jos yhtälön nimenä on yht, niin yht[[1]] on sen vasen ja yht[[2]] oikea puoli.)
- 18. Ratkaise yhtälöiden
- 1.
- 168x = 195
- 2.
- x2 − 2x − 4 = 0
- 3.
- x3 − x2 + x − 21 = 0
- 4.
- (a − b)x2 + ax + b = 0
kaikki juuret. Sijoita juuret takaisin yhtälöihin ja tutki, toteutuvatko yhtälöt. Vihje: Talleta ensin yhtälö jollekin nimelle. Yhtälöissä käytetään yhtäläisyysmerkkinä ==. Yhtälön ratkaiseminen Solve-funktiolla tuottaa ratkaisut ns. korvaussääntöjen muodossa. Näiden avulla voidaan saadut juuret helposti sijoittaa mihin tahansa lausekkeeseen, esimerkiksi yhtälöön: yhtalo/.korvaus. Tässä /. on lyhennemerkintä Mathematican funktiolle ReplaceAll.
