
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Mathematica harjoitustehtäviä liittyen grafiikkaan Mathematicassa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se Mathematica-pääsivulta löytyvään harjoituspohjaan.
- 1. Piirrä funktion f(x) = sin 8x + sin 9x kuvaaja. Vihje: Tarkastele riittävän pitkää väliä. Muista merkinnät: Sin[8x] etc.
- 2. Tšebyševin polynomit määritellään välillä [−1, 1] lausekkeella
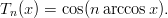
Piirrä polynomien Tn, n = 1, 2, 3, 4, 5, kuvaajat samaan kuvioon. Vihje: Funktioiden nimet ovat Cos ja ArcCos. Yhden kuvaajan piirtäminen tapahtuu komennolla Plot. Useita kuvioita voidaan yhdistää samaan kuvaan komennolla Show, jonka argumenteiksi kirjoitetaan ne tulosteet, jotka kuvaan halutaan. Esimerkiksi %k viittaa tulosteeseen Out[k]; tulosteille voidaan antaa myös nimet kirjoittamalla esimerkiksi kuva1 = Plot ....
- 3. Piirrä sini- ja kosinifunktioiden kuvaajat muotoaPlot[–Sin[x], Cos[x]˝, –x, -Pi, Pi˝,
PlotStyle -> –Dashing[–0.1, 0.05˝],
–RGBColor[0.9, 0.3, 0.4], Thickness[0.05]˝˝olevalla käskyllä. Selvitä kokeilemalla, mitä PlotStyle-määrittelyssä olevat parametrit vaikuttavat kuvioon. Vihje: Parametrien merkitystä voi tutkia myös Mathematican dokumentaatiosta.
- 4. Piirrä funtion f(x,y) = x3 − 2y2 − 5x kuvaaja. Vihje: Tarvittava funktio on Plot3D. Tutki piirtoalueen vaikutusta kuvaajan muotoon ja miten siihen voidaan vaikuttaa Plot3D-funktion optioilla (katso dokumentaatiota).
- 5. Piirrä funtion f(x,y) = arctan(y∕x) kuvaaja. Miten funktio käyttäytyy origon ympäristössä? Miten funktion voi luonnehtia geometrisesti? Onko funktio jatkuva? Vihje: Funktionnimi on ArcTan. Tarvittava piirtokomento on Plot3D. Piirtotiheyttä voi säätää optioilla PlotPoints tai Mesh. Muitakin optioita on; katso dokumentaatiota.
- 6. Piirrä kahden muuttujan funktion f(x,y) = log yx kuvaaja. Vihje: Mieti ensin, millä arvoilla (x,y) funktio on määritelty.
- 7. Piirrä kahden muuttujan funktion
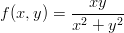
kuvaaja. Tutki erityisesti funktion käyttäytymistä origon ympäristössä. Vihje: Käytä sekä funktiota Plot3D että funktiota ParametricPlot3D. Voitaisiinko käyttää napakoordinaatteja? Säädä piirtotiheys sopivaksi optiolla Mesh. Onko funktio jatkuva origossa?
- 8. Piirrä kuva parametrimuodossa annetusta käyrästä
![x = cospt, y = sin qt, t ∈ [0,2π ],](mathematicaHarGrafiikka2x.png)
missä p ja q ovat numeerisia kertoimia. Vihje: Piirtokomento on ParametricPlot. Tutki myös, mitä optioita on käytettävissä.
- 9. Piirrä kuva parametrimuodossa annetusta kolmiulotteisen avaruuden käyrästä
![x = (5 + cos25t) cos5t, y = (5 + cos25t)sin5t, z = sin25t, t ∈ [0,2π].](mathematicaHarGrafiikka3x.png)
Vihje: Piirtokomento on ParametricPlot3D.
- 10. Piirrä kuva parametrimuodossa annetusta kolmiulotteisen avaruuden käyrästä
![x = (2π − t)cos 5t, y = (2π − t) sin 5t, z = t, t ∈ [0,2π ].](mathematicaHarGrafiikka4x.png)
Muunna parametriesitystä siten, että saadaan pallopinnalla sijaitseva spiraali. Vihje: Piirtokomento on ParametricPlot3D. Piirtotiheyttä voidaan säätää optiolla PlotPoints. Pallopinta: Jos korkeuskoordinaatti on t, niin mikä on pisteen etäisyys z-akselista?
- 11. Piirrä alueessa −25 ≤ x ≤ 25, −5 ≤ y ≤ 5 kuva käyrästä x = y3 − 5y2 + y + 3 ParametricPlot-funktiolla. Vihje: Valitse parametriksi y.
- 12. Piirrä kuva parametrimuodossa annetusta ruuvipinnasta:
![-v- v-- 1-
x = u(1 − 8π )cos v, y = u (1 − 8π) sin v, z = 5 (v − u), u ∈ [0,3], v ∈ [0,8π ].](mathematicaHarGrafiikka5x.png)
Vihje: Piirtokomento on ParametricPlot3D. Säädä piirtotiheys sopivaksi, niin että saat kauniin kuvan: optio Mesh.
- 13. Tutki, millaista pintaa esittää parametriesitys
![x = cosu (a + b cosv), y = sinu(a + b cosv), z = bsinv, u ∈ [0,2π], v ∈ [0,2π ].](mathematicaHarGrafiikka6x.png)
Anna piirtämistä varten vakioille a ja b erilaisia (positiivisia) arvoja ja yritä päästä selville niiden merkityksestä. Tutki myös, mitä vaikuttaa optio Shading->False grafiikkakomennossa. Vihje: Tutki aluksi tapausta, missä a∕b = 2, mutta tarkastele myös tapauksia, missä suhde on = 1 tai < 1. Pinnasta saa paremman käsityksen piirtämällä siitä vain sopivan osan, ts. rajoittamalla parametrien u ja v vaihteluväliä.
- 14. Yhtälö
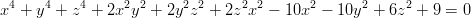
esittää erästä kolmiulotteisen avaruuden pintaa, ympyrärengasta eli torusta. Leikkaa pintaa tasoilla z = vakio ja x = vakio ja piirrä leikkauskäyrät. Vihje: Käytä funktiota ContourPlot. Millaisia kvalitatiivisesti erilaisia leikkauskäyriä syntyy?
- 15. Piirrä origon ympäristössä kuva käyrästä y4 + y2 + xy = x3 − x. Vihje: Käytä funktiota ContourPlot.
- 16. Tutki, mitkä xy-tason pisteet toteuttavat yhtälön log yx = log xy. Piirrä kuvio. Vihje: Logaritmifunktio on Log. Käytä funktiota ContourPlot. Mieti, mikä on sopiva piirtoalue.
- 17. Tutki funktion f(x,y) = yx käyttäytymistä origon ympäristössä alueessa x > 0, y > 0: piirrä kuvaaja (pinta), piirrä pinnan korkeuskäyriä, laske funktion arvoja. Mitä arvoja funktio saa origoa lähestyttäessä? Vihje: Tarvittavia funktioita: Plot3D, ContourPlot. Jälkimmäiselle voidaan antaa optiona korkeuskäyrien korkeudet muodossa Contours->{...}, missä korkeudet luetellaan listassa; katso myös dokumentaatiota.
- 18. Piirrä origon ympäristössä kuva pinnasta x3 + y3 + z3 −x2yz −xy2z −xyz2 − 1 = 0. Vihje: Käytä funktiota ContourPlot3D. Katso dokumentaatiosta käyttöohjeet.
