
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Mathematica harjoitustehtäviä liittyen funktioihin ja funktionkäsittelyyn Mathematicassa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se Mathematica-pääsivulta löytyvään harjoituspohjaan.
- 1. Mathematica tuntee ns. gammafunktion Γ(x) nimellä Gamma. Piirrä tämän ja sen derivaatan kuvaajat. Mitä arvoja funktio saa positiivisilla kokonaislukuarvoilla? Vihje: Skaalaa graafinen esitys siten, että kuvaajien luonne tulee selkeästi näkyviin. Funktion arvot positiivisilla kokonaislukuarvoilla voidaan ilmaista yksinkertaisesti. Miten?
- 2. Määrittele Mathematicalle funktio
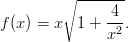
Laske funktion arvo pisteissä x = −1, 0, 1. Piirrä kuvaaja. Mikä funktion raja-arvo origossa? Onko tämä olemassa? Onko funktio jatkuva? Vihje: Funktion määrittelyssä voidaan tässä tapauksessa käyttää yhtä hyvin merkkiä = tai merkkiä :=. Raja-arvo voidaan laskea myös funktiolla Limit; katso ohjeet dokumentaatiosta ja kokeile.
- 3. Piirrä funktion log x2 kuvaaja ja laske sen derivaatta. Voidaanko funktio lausua luonnollisen logaritmin avulla? Vihje: Mathematican funktio Log on luonnollinen logaritmi. log kx merkitään Log[k,x]. Ks. myös dokumentaatiota.
- 4. Mathematicassa on kaksi operaattoria, joita voidaan käyttää funktioiden määrittelyssä: joko = (eli Set) tai := (eli SetDelayed). Yritä selvittää näiden ero määrittelemällä kaksi funktiota seuraavasti:f[x˙,n˙]= Expand[x^n]
g[x˙,n˙]:= Expand[x^n]Laske tämän jälkeen f[a+b,5] ja g[a+b,5]. Vihje: Delay = viivästää. Katso myös Mathematican dokumentaatiota. Huomaa, että Expand ei kehitä (ei voi kehittää) lauseketta, jonka eksponentti on symboli: Kokeile g[a+b,n].
- 5. Määrittele Mathematicalle funktio
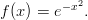
Laske taulukko sen arvoista välillä [0, 5] askelena 0.1. Piirrä funktion derivaatan kuvaaja. Muodosta integraalifunktio ja piirrä sen kuvaaja. Laske funktion integraali yli reaaliakselin. Katso, mitä antaa komento ?f. Vihje: Funktio voidaan määritellä kahdella tavalla: antamalla muotoa f[x_]:= ... oleva määrittely tai käyttämällä funktiota Function. Kokeile molempia. Taulukko muodostetaan funktiolla Table, derivaatta saadaan esimerkiksi kirjoittamalla f’[x]. Integroinnissa tarvittava äärettömyys on Infinity; se voidaan myös valita paletista.
- 6. Määrittele Mathematicalle funktio
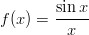
ja laske sen arvot pisteissä x = π∕2, x = 1 ja x = 0. Määrittele tämän jälkeen funktio origossa siten, että siitä tulee jatkuva. Laske uudelleen sen arvo origossa. Piirrä funktion kuvaaja ja kokeile, miten Mathematica tulkitsee syötteen f’[x]. Mitä on f’[0]? Katso, mitä antaa komento ?f. Vihje: Funktio voidaan määritellä kahdella tavalla: antamalla muotoa f[x_]:= ... oleva määrittely tai käyttämällä funktiota Function. Edellistä tapaa käytettäessä voidaan lisäksi määritellä erikseen arvo yksittäisissä pisteissä: f[0]= ... .
- 7. Määrittele Mathematicalle funktio, jonka kuvaaja välillä [0,
 ] yhdistää pisteet
(0, 0) ja (
] yhdistää pisteet
(0, 0) ja ( , 2) sekä välillä [
, 2) sekä välillä [ , 1] pisteet (
, 1] pisteet ( , 2) ja (1, 0). Muualla funktio on = 0. Piirrä
funktion kuvaaja.
Vihje: Funktion paloittaisessa määrittelyssä käytetään symbolia /; rajoittamaan
määrittelyaluetta, esimerkiksi f[x_/;x > -1 && x ¡ 1]:= ... . Vaihtoehtona on käyttää funktiota
Piecewise.
, 2) ja (1, 0). Muualla funktio on = 0. Piirrä
funktion kuvaaja.
Vihje: Funktion paloittaisessa määrittelyssä käytetään symbolia /; rajoittamaan
määrittelyaluetta, esimerkiksi f[x_/;x > -1 && x ¡ 1]:= ... . Vaihtoehtona on käyttää funktiota
Piecewise.
- 8. Määrittele Mathematicalle seuraava funktio ja piirrä sen kuvaaja:
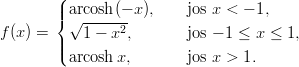
Katso, mitä antaa komento ?f. Onko funktio jatkuva? Entä derivoituva? Osaako Mathematica laskea sen derivaatan? Vihje: Huomaa: Hyperbolisen kosinin käänteisfunktio (päähaara) arcosh on Mathematicassa (virheellisesti) ArcCosh. Funktion paloittaisessa määrittelyssä käytetään symbolia /; rajoittamaan määrittelyaluetta, esimerkiksi f[x_/;x > -1 && x ¡ 1]:= ... . Myös funktiota Piecewise voidaan käyttää.
- 9. Määrittele cos(nx) kahden muuttujan x ja n funktiona. Piirrä tätä käyttäen funktioiden cos x, cos 2x ja cos 4x kuvaajat samaan kuvioon. Vihje: Helpointa on piirtää kukin kuvaaja erikseen ja yhdistää kuviot Show-komennolla yhdeksi kuvioksi. Kuvion voi piirtää myös yhdellä Plot-komennolla.
- 10. Määrittele Mathematicalle kahden muuttujan funktio, jonka kuvaaja välillä [0,
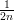 ]
yhdistää pisteet (0, 0) ja (
]
yhdistää pisteet (0, 0) ja (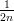 , 2n) sekä välillä [
, 2n) sekä välillä [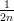 ,
, ] pisteet (
] pisteet (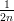 , 2n) ja (
, 2n) ja ( , 0).
Muualla funktio on = 0. Piirrä funktion kuvaaja.
Vihje: Funktion paloittaisessa määrittelyssä tarvittavat ehdot voidaan sijoittaa myös
määrittelevän lausekkeen jälkeen, esimerkiksi f[x_,_n]:=4 n^2 x/;x >= 0 && x ¡= 1/(2 n).
, 0).
Muualla funktio on = 0. Piirrä funktion kuvaaja.
Vihje: Funktion paloittaisessa määrittelyssä tarvittavat ehdot voidaan sijoittaa myös
määrittelevän lausekkeen jälkeen, esimerkiksi f[x_,_n]:=4 n^2 x/;x >= 0 && x ¡= 1/(2 n).
- 11. Laske derivoimalla yhdistetyn funktion f(g(x)) ensimmäinen, toinen ja kolmas derivaatta. Vihje: Yhdistettyä funktiota voidaan käsitellä suoraan muodossa f[g[x]]. Saisitko samat tulokset laskemalla käsin?
- 12. Jos g on funktion f käänteisfunktio, on kaikilla arvoilla x voimassa f(g(x)) = x. Derivoi tätä yhtälöä kahdesti ja ratkaise tuloksista lausekkeet funktion g ensimmäiselle ja toiselle derivaatalle lausuttuina funktion f derivaattojen ja funktion g arvon g(x) avulla. Vihje: Derivointi voidaan suoran kohdistaa yhtälöön: D[f[g[x]]==x,x]. Tulokset: g′(x) =
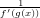 ,
g′′(x) = −
,
g′′(x) = −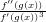 . Saatko samat tulokset laskemalla käsin?
. Saatko samat tulokset laskemalla käsin?
- 13. Määrittele Mathematicalle funktio
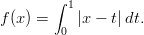
Piirrä tämän määritelmän perusteella funktion ja sen derivaatan kuvaajat. Vihje: Itseisarvofunktio (Abs) integraalin sisällä saattaa aiheuttaa ongelmia. Kokeile itseisarvojen käyttöä, mutta määrittele funktio myös paloittain itseisarvolausekkeen merkkien mukaan kolmessa osassa. Tutki, osaako Mathematica derivoida määrittelemiäsi funktioita.
- 14. Ratkaise toisen asteen ax2 + 2x + 1 = 0 yhtälö ja määrittele funktiot, jotka esittävät yhtälön juuria kertoimen a funktioina. Piirrä näiden funktioiden kuvaajat. Missä alueessa funktiot ovat määriteltyjä? Miten ne käyttäytyvät, kun a → 0, jolloin yhtälö muuttuu ensimmäisen asteen yhtälöksi? Vihje: Ratkaise yhtälö Solve-komennolla ja käytä tulosta suoraan funktioiden määrittelyssä. Funktionmäärittelyssä on syytä käyttää merkkiä = eikä :=. (Miksi?)
- 15. Fibonaccin luvut määritellään ehdoilla a0 = 1, a1 = 1, an = an−1 + an−2 (n = 2, 3, 4,…). Määrittele Mathematican funktio, joka laskee Fibonaccin lukuja antamalla määrittelyt a[0]=1; a[1]=1; a[n_]:=a[n-1]+a[n-2] ja laske tämän avulla Fibonaccin luvut a10 ja a20. Muodosta myös taulukko, jossa on 20 ensimmäistä lukua. Vihje: Ennen Mathematican funktion a määrittelyä anna komento Remove[a], jolla poistetaan mahdolliset aiemmat määrittelyt. Katso myös, mitä komento ?a määrittelyn jälkeen antaa. Kyseessä on rekursiivinen funktiomäärittely. Taulukko voidaan muodostaa funktiolla Table. Miksi taulukon laskeminen kestää?
- 16. Funktio f : ℕ → ℕ määritellään ehdoilla
Tutki, mitä arvoja funktio saa. Vihje: Funktion arvot voidaan laskea taulukkoon Table-funktiolla. Miten laskisit käsin arvon f(1)?f(n) = n − 5, kun n > 10, f(n) = f(f(n + 6)), kun 1 ≤ n ≤ 10. - 17. Olkoot A ja B äärellisen monen alkion joukkoja. Joukossa A on m alkiota ja joukossa B on n alkiota. Olkoon S(m,n) surjektioiden A → B lukumäärä. Tälle pätee
Muodosta surjektioiden määrän osoittava taulukko, kun 1 ≤ m ≤ 5, 1 ≤ n ≤ 5. Onko itsestään selvää, mitkä taulukon alkiot ovat = 0? Miksi? Mitä lukuja ovat taulukon lävistäjäalkiot? Osaatko päätellä kaavojen pätevyyden? Vihje: Surjektio A → B on funktio, jossa jokainen maalijoukon B alkio on jonkin alkion kuva. Summa voidaan muodostaa funktiolla Sum, binomikerroin on Binomial. Taulukon (kaksinkertaisen listan) voi muodostaa Table-komennolla ja sen saa näkymään kaksiulotteisena kirjoittamalla perään //TableForm.S(m, 1) = 1, S(m,n) = nm −∑ k=1n−1 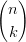 S(m,k), n = 2, 3,….
S(m,k), n = 2, 3,…. - 18. Mathematicalle voidaan määritellä myös monimutkaisempia funktioita funktioidenmäärittelyfunktion Function avulla. Määrittele funktio f asettamalla
![f = Function [x,FactorInteger [x ][[1,1 ]]]](mathematicaHarFunktiot18x.png)
ja tutki, mitä se laskee, kun argumenttina on luonnollinen luku. Vihje: Tutki erikseen, mitä FactorInteger antaa. Indeksimerkintä [[1,1]] poimii sen tulostuksesta osan.
