
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Mathematica harjoitustehtäviä liittyen differentiaali ja integraalilaskentaan.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se Mathematica-pääsivulta löytyvään harjoituspohjaan.
- 1. Laske integraali
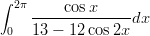
a) symbolisesti, b) numeerisesti. Piirrä integroitavan funktion kuvaaja. Mikä itse asiassa on integraalin arvo? Vihje: Symbolinen integrointi tapahtuu funktiolla Integrate, numeerinen funktiolla
NIntegrate. Jälkimmäisessä sovelletaan suoraan jotakin numeerisen integroinnin menetelmää, jonka valintaan myös käyttäjä voi vaikuttaa. Ks. dokumentaatiota, erityisesti Implementation Notes. - 2. Määritä funktion
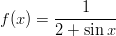
integraalifunktio ja piirrä sen kuvaaja. Onko tämä jatkuva? Pitäisikö sen olla jatkuva? Laske funktion integraali jakson [0, 2π] yli a) integroimalla analyyttisesti komennolla Integrate, b) integroimalla numeerisesti komennolla NIntegrate, c) muodostamalla ensin integraalifunktio komennolla Integrate ja sijoittamalla rajat tähän korvausoperaattoria käyttäen. Vihje: Komennolla Integrate lasketaan sekä integraalifunktio että määrätty integraali. Numeeriselle integroinnille (määrätyn integraalin laskemiseen) on komento NIntegrate. Korvausoperaattori on ReplaceAll eli /. .
- 3. Määritä funktion f(x) = x4 − 7x3 + 11x2 + 7x − 10 nollakohdat, ääriarvopisteet ja käännepisteet. Piirrä kuvaaja. Vihje: Talleta aluksi funktion lauseke jollakin nimellä, jotta siihen viittaaminen myöhemmin on helppoa. Tarvittavia funktioita: D; Solve, NSolve. Arvojen sijoittaminen johonkin lausekkeeseen tapahtuu korvausoperaattorilla /. eli ReplaceAll. Mikäli saadut numeeriset lausekkeet näyttävät hankalilta, ne voi hahmottaa paremmin laskemalla likiarvot funktiolla N. Myös funktiosta Chop saattaa olla iloa; ks. dokumentaatiota.
- 4. Määritä funktion f(x) = 2x4 − 12x3 + 7x2 + 41x − 3 reaaliset nollakohdat, ääriarvokohdat ja ääriarvot sekä käännepisteet. Vihje: Piirrä kuvio. Ovatko tarkat arvot löydettävissä?
- 5. Määritä funktion f(x) = arcsin(2x
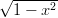 ) suurin ja pienin arvo välillä [−1, 1].
Vihje: arcsin on Mathematicassa ArcSin. Piirrä myös kuvio.
) suurin ja pienin arvo välillä [−1, 1].
Vihje: arcsin on Mathematicassa ArcSin. Piirrä myös kuvio.
- 6. Laske funktion funktion f(x) = 2x4 − 12x3 + 7x2 + 41x − 3 kuvaajan ja x-akselin rajaaman alueen pinta-ala. Vihje: Piirrä kuvio. Siirry tarvittaessa numeeriseen laskentaan.
- 7. Laske sen alueen pinta-ala, jota rajoittavat käyrät y = x2 − 3 ja y =
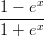 .
Vihje: Siirry tarvittaessa numeeriseen laskentaan.
.
Vihje: Siirry tarvittaessa numeeriseen laskentaan.
- 8. Ohjelmat:
Maple,Mathematica
(Kurssi: 2012 kevät H/H2T2.tex)Laske sen alueen pinta-ala, jota rajoittavat käyrät y2 = x ja x − y = 3. Vihje: Mieti, kumpi on helpompaa: integrointi x- vai y-suunnassa. Ratkaisu: mplDi02.pdf (pdf-tiedosto),
mplDi02.mw (Maple ws)
mmaDi107R.nb (Mma-notebook)
Luokittelu:
mplteht/mplDiffint/mplDi02.tex, mmateht/mmaDiffint/mmaDi107.tex
Avainsanat:
Pinta-ala, integraali,diffint perusteet. - 9. Laske käyrien y = x3 − 3x ja y = −x3 + x rajoittaman kaksiosaisen alueen pinta-ala. Vihje: Piirrä kuvio. Määritä integroimisrajat. Varsinainen integrointi voidaan tehdä monella eri tavalla: integroimalla symbolisesti tai numeerisesti, integroimalla funktioiden erotuksia tai erotuksen itseisarvoa.
- 10. Käyrä y = sin 2x, x ∈ [0,π], pyörähtää x-akselin ympäri. Laske syntyvän pyörähdyskappaleen tilavuus ja pinnan ala. Parametrisoi pinta ja piirrä se. Vihje: Valitse parametrisoinnissa toiseksi parametriksi x ja toiseksi pyörähdyskulma. Piirtäminen funktiolla ParametricPlot3D. Muista: Sin[x]^2 jne.
- 11. Paraabelin y = −4x2 + 40x − 97 ja x-akselin rajoittama alue pyörähtää y-akselin ympäri. Laske syntyvän kappaleen tilavuus. Vihje: Kappaleen voi ajatella muodostuvan joko vaakasuorista tasoleikkauksista tai lieriöpinnoista, joiden akselina on y-akseli. Nämä johtavat kahteen erilaiseen integraaliin, jotka luonnollisestikin antavat saman tuloksen.
- 12. Laske sen pyörähdyskappaleen tilavuus, joka syntyy käyrän y = x3 + 1, x”=akselin sekä suorien x = 3 ja y = 9 rajoittaman alueen pyörähtäessä suoran x = 3 ympäri. Vihje: Periaatteessa yksinkertainen integrointi, mutta tutki tarkoin, mitä funktiota on integroitava.
- 13. Puutarhuri viljelee tomaatteja, joiden muoto määräytyy kardioidin r = a(1 + cos φ) pyörähtämisestä x-akselin ympäri. Piirrä kardioidi. Laske tomaatin tilavuus. Tuntuuko saamasi tilavuus uskottavalta? Anna vakiolle a jokin lukuarvo ja laske vastaava tilavuuden likiarvo. Piirrä kuvio tomaatista. Vihje: Valitse kardioidin parametrisoinnissa napakulma φ parametriksi, lausu x ja y tämän avulla ja käytä funktiota ParametricPlot. Vaihtoehtona on käyttää funktiota PolarPlot. Tomaattipinnan parametrisoinnissa ota parametreiksi napakulma φ ja pyörähdyskulma x-akselin ympäri. Piirtäminen tapahtuu funktiolla ParametricPlot3D. Tilavuus saadaan periaatteessa integraalista∫ y2dx, johon on tehtävä sellaiset sijoitukset, että muuttujaksi saadaan napakulma φ.
- 14. Laske kardioidin r = 1 + cos φ kaarenpituus. Piirrä kuvio. Miten saat kardioidin kuvan oikeanmuotoiseksi? Tuntuuko saamasi pituus uskottavalta? Vihje: Kaarenpituusintegraali: ∫ ds = ∫
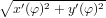 dφ.
dφ.
- 15. Piirrä avaruuskäyrä
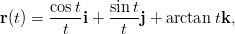
kun t ∈ [1,T] ja T = 100. Määritä käyrän kaarenpituus ja tutki, onko sillä raja-arvoa, kun T →∞. Vihje: Käyrä on luontevinta kirjoittaa vektoriksi r = {Cos[t]/t,Sin[t]/t,ArcTan[t]} ja laskea kaarenpituus integraalista ∫ |r′(t)|dt.
- 16. Astia on kärjellään seisova avonainen ympyräkartio. Kartion pohjan säde on 6,6 cm ja sivujana 11,0 cm. Astia on täynnä vettä. Astiaan asetetaan pallo, joka sivuaa kartion vaippaa. Määritä pallon säde siten, että astiasta valuva vesimäärä on mahdollisimman suuri. Vihje: Laskusta tulee selkeämpi, jos se lasketaan symboleja käyttäen ja vasta lopuksi asetetaan näille arvot. Arvojen sijoittamiseksi on luontevaa määritellä korvaussääntö {r->6.6, s->11.0, h->Sqrt[11.0^2-6.6^2]}, jolloin arvot voidaan helposti sijoittaa mihin tahansa välitulokseenkin ja tämän jälkeen jatkaa laskua symboleilla.
- 17. R-säteisen pallon ympäri asetetaan mahdollisimman pieni neliöpohjainen suora pyramidi siten, että pallo sivuaa pyramidin pohjaa ja sivutahkoja. Laske pallon tilavuuden suhde pyramidin tilavuuteen. Vihje: Lausu pyramidin tilavuus sopivan muuttujan avulla. Tätä varten tarvitaan sopivien kolmioiden yhdenmuotoisuutta. Hyödynnä Mathematican komentoja, jotta et joudu syöttämään käsin aiempien laskujen tuloksia!
- 18. Osoita, että käyrän y = e−x sin x ja x-akselin alueessa x ≥ 0 rajoittamien alueiden A0, A1, A2, … pinta-alat muodostavat geometrisen jonon. Laske integraali∫ 0∞|e−x sin x|dx. Vihje: Määrittele alueen An pinta-ala funktioksi: a[n_]:=... ja sievennä (Simplify,
FullSimplify) peräkkäisten alojen suhteen lauseke. Funktiolla Sum voi laskea myös äärettömän monen termin summia. - 19. Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = ax2. Suoran kulman kärkeen asetetaan paraabelin normaali. Osoita, että kolmion hypotenuusa leikkaa normaalin samassa pisteessä riippumatta kolmion kahden muun kärjen sijainnista. Määritä leikkauspiste. Vihje: Esimerkiksi: Laske leikkauspiste, kun suoran kulman kärjen x-koordinaatti on t ja toisen kateetin kulmakerroin on k.
- 20. Pallon muotoiseen nestesäiliöön, jonka säde on yksi metri, pumpataan nestettä nopeudella 10 litraa sekunnissa. Piirrä kuvaaja, joka esittää nestepinnan korkeutta säiliössä ajan funktiona. Kuinka kauan säiliön täyttäminen kestää? Piirrä nestepinnan korkeuden nousunopeuden kuvaaja. Vihje: Ratkaise nestepinnan korkeus nestetilavuuden funktiona ja valitse saaduista ratkaisuista oikea. Lauseke on hankala, mutta Mathematica pystyy kuitenkin käsittelemään sitä.
- 21. Muodosta kuusi satunnaislukua, jotka ovat peräisin välien [−5,−3], [−2,−1], [1, 2], [3, 5], [−0.5, 0.5] ja [1, 2] tasaisesta jakaumasta. Näistä neljä ensimmäistä olkoot neljännen asteen polynomin nollakohdat, kaksi viimeistä määrittävät pisteen, jonka kautta polynomin kuvaaja kulkee. Suurimman ja pienimmän nollakohdan välisellä alueella polynomin kuvaaja pyörähtää x-akselin ympäri ja muodostaa pyörähdyskappaleen. Laske tämän tilavuus ja pinta-ala; piirrä kuvio. Vihje: Satunnaislukuja generoidaan funktiolla RandomReal, jolle voidaan antaa argumentiksi mm. väli, jolta lukuja halutaan.
- 22. Derivoi funktiot xn, xx, sin 4x + cos 4x. Integroi saamasi tulokset. Päädytäänkö takaisin samaan funktioon, josta lähdettiin? Vihje: Huomaa merkintä: Sin[x]^4 etc. Kahden lausekkeen samuutta voi tutkia tarkastelemalla niiden erotusta. Tämän vertaaminen nollaan on yleensä helpompaa kuin kahden monimutkaisen lausekkeen vertaaminen toisiinsa. Toisena vaihtoehtona on tarkastella lausekkeiden kuvaajia.
- 23. Laske funktion f(x) =
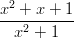 kahdeskymmenes derivaatta ja tälle sekä tarkka arvo
että likiarvo pisteessä x = 5.
Vihje: Yritä suoriutua mahdollisimman vähillä Mathematican käskyillä!
kahdeskymmenes derivaatta ja tälle sekä tarkka arvo
että likiarvo pisteessä x = 5.
Vihje: Yritä suoriutua mahdollisimman vähillä Mathematican käskyillä!
- 24. Muodosta funktion tan x kertalukuja 1, 2,…, 20 olevat derivaatat. Mikä on kertalukua 10 olevan derivaatan arvo origossa? Vihje: Helpointa on muodostaa derivaatoista lista. Jos listan nimi on lst, sen k:s alkio on lst[[k]]. Mathematica käyttää trigonometrisia funktioita sekantti sec ja kosekantti csc. Nämä määritellään yksinkertaisesti: secx =
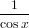 , cscx =
, cscx = 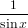 .
.
- 25. Laske funktion f(x) = x2 sin(1∕x) derivaatta jokaisessa pisteessä x ∈ ℝ. Onko derivaattafunktio jatkuva? Piirrä sen kuvaaja. Vihje: Funktio on derivoituva myös origossa, mutta derivaatta on laskettava erotusosamäärän raja-arvona (miksi?). Mathematicassa on valmiina funktio Limit.
- 26. Olkoot f ja g derivoituvia funktioita. Laske tulon ja yhdistetyn funktion derivaatat, so. derivoi lausekkeet f(x)g(x) ja f(g(x)). Vihje: Poista ensin funktioille mahdollisesti aiemmin tehdyt määrittelyt: Remove[f,g]. Määräämätön funktio voidaan ottaa käyttöön yksinkertaisesti kirjoittamalla f[x].
- 27. Olkoon f, g ja h derivoituvia kahden muuttujan funktioita. Laske yhdistetyn funktion f(g(x,y),h(x,y)) osittaisderivaatat. Ovatko saadut lausekkeet sitä, mitä pitäisi? Vihje: Määräämätön funktio voidaan ottaa käyttöön kirjoittamalla f[x,y]. Jos olet aiemmin käyttänyt samaa symbolia jossakin muussa merkityksessä, hävitä se ensin: Remove[f]. Derivointioperaattori on D riippumatta siitä, lasketaanko tavallisia vai osittaisderivaattoja.
- 28. Yhtälö x = y3 + y2 + y + 1 määrittelee funktion y(x), joka origossa saa arvon −1. Laske implisiittisellä derivoinnilla y′(0). Vihje: Sijoita yhtälöön y:n paikalle y(x) ja derivoi yhtälö.
- 29. Laske funktion f(x) = arctan x + arctan
 derivaatta ja saata se mahdollisimman
yksinkertaiseen muotoon. Mitä tästä voidaan päätellä?
Vihje: arctan on Mathematicassa ArcTan. Piirrä myös kuvio.
derivaatta ja saata se mahdollisimman
yksinkertaiseen muotoon. Mitä tästä voidaan päätellä?
Vihje: arctan on Mathematicassa ArcTan. Piirrä myös kuvio.
- 30. Muodosta funktion f(x) = arctan
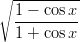 ensimmäinen ja toinen derivaatta. Piirrä
näiden kuvaajat.
Vihje: arctan on Mathematicassa ArcTan.
ensimmäinen ja toinen derivaatta. Piirrä
näiden kuvaajat.
Vihje: arctan on Mathematicassa ArcTan.
- 31. Integroi funktio xn. Onko tulos oikein kaikilla n? Onko samantekevää, jos jollekin symbolille ensin annetaan arvo ja sitten muokataan symbolin sisältävää lauseketta, tai jos ensin muokataan lauseketta ja vasta sitten annetaan symbolille arvo? Vihje: Kokeile: Integrate[x^n/.n->-1,x] == Integrate[x^n,x]/.n->-1. Sijoita myös muuttujalle n jokin muu arvo. Miten selität tulokset?
- 32. Etsi funktion e−x2 integraalifunktio. Laske määrätyt integraalit

Määritä näille myös likiarvot. Mitä saatu integraalifunktion lauseke tarkoittaa? Vihje: Funktiolla Integrate lasketaan sekä integraalifunktioita että määrättyjä integraaleja. Äärettömyys on Infinity; se voidaan myös valita paletista. Mathematica tuntee monia muitakin funktioita kuin ns. tavalliset alkeisfunktiot. Mitä nämä oikeastaan ovat, ei aina ilmene dokumentaatiosta, koska määritelmät eivät välttämättä ole yksinkertaisia.
- 33. Laske integraalit
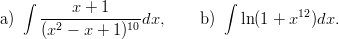
Ovatko Mathematican antamat tulokset oikein? Miten nämä voisi tarkistaa? Millaista menetelmää pitäisi käsinlaskussa käyttää? Vihje: Symbolisissa ohjelmissa derivointi on yleensä integrointia luotettavampaa. Tarkistus voi siis tapahtua derivoimalla. Logaritmifunktio on Log; ks. dokumentaatiota.
