
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Mathematica harjoitustehtäviä liittyen vektorianalyysiin.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se Mathematica-pääsivulta löytyvään harjoituspohjaan.
- 1. Osoita, että polynomit x2 + x ja x2 + 1 toteuttavat differentiaaliyhtälön (x2 − 2x − 1)y′′− 2(x − 1)y′ + 2y = 0. Vihje: Talleta differentiaaliyhtälö Mathematican muistiin siten, että funktion y argumentit ovat paikoillaan: y’’[x] jne. Määrittele vuorollaan kumpikin polynomi Mathematican funktioksi (p[x_]:= ...) ja sijoita tämä yhtälöön: (yhtalo/.y->p). Sievennä tarvittaessa.
- 2. Osoita, että funktio
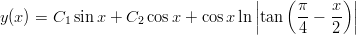
toteuttaa differentiaaliyhtälön y′′ + y = tan x. Luvut C1 ja C2 ovat vakioita. Vihje: Joko: Muodosta funktion y ja erikseen lasketun toisen derivaatan summa ja sievennä tämä. Tai: Määrittele y Mathematican funktioksi ja sievennä y’’[x] + y[x]. Logaritmifunktio on Log. Itseisarvot voidaan jättää huomiotta, sillä Mathematica tuntee logaritmifunktion ln x myös negatiivisilla argumenteilla x, jolloin se eroaa funktiosta ln |x| vain kompleksisella vakiolla iπ. Kokeile: FullSimplify[ComplexExpand[Log[-x]], x > 0].
- 3. Ratkaise differentiaaliyhtälö y′′ + y = x2. Etsi myös alkuehtoa y(0) = 1, y′(0) = 2 vastaava yksittäisratkaisu. Vihje: Käytä komentoa DSolve, jonka avulla voidaan löytää sekä yleinen ratkaisu että yksittäisratkaisu.
- 4. Etsi yleinen ratkaisu Airyn differentiaaliyhtälölle y′′− xy = 0. Mitä ratkaisussa esiintyvät funktiot ovat? Vihje: Käytä komentoa DSolve. Ratkaisu ei ole lausuttavissa tavallisten alkeisfunktioiden avulla, mutta kylläkin Mathematican tuntemien funktioiden avulla.
- 5. Kesätapahtumassa hyttysten määrä oli tilaisuuden alussa 200 ja kolme tuntia myöhemmin 700. Määrän kasvunopeus hetkellä t oli suoraan verrannollinen hyttysten määrään sinä hetkenä. Muodosta hyttysten määrää kuvaava differentiaaliyhtälö ja sen ratkaisuna hyttysten määrä mielivaltaisella hetkellä t. Mikä oli hyttysten määrä viiden tunnin kuluttua tilaisuuden alkamisesta? Vihje: Käytä funktioita DSolve ja Solve. Kumpikin antaa ratkaisun korvaussäännön muodossa. Ratkaisu voidaan tallettaa muuttujaksi jatkokäsittelyä varten korvausoperaattorilla, esimerkiksi lukum= y[t]/.ratkaisu.
- 6. Lohenviljelyaltaaseen, jossa oli 1100 kalaa, levisi kalatauti. Taudin vaikutuksesta kalamäärä alkoi vähetä yhtälön
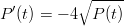
mukaisesti. Tässä P(t) on kalamäärä hetkellä t, ja aika t on mitattu viikkoina. Kuinka monen viikon kuluttua kaikki kalat olivat kuolleet? Vihje: Käytä funktioita DSolve ja Solve. Kumpikin antaa ratkaisun korvaussäännön muodossa. Ratkaisu voidaan tallettaa muuttujaksi jatkokäsittelyä varten korvausoperaattorilla, esimerkiksi lukum= y[t]/.ratkaisu.
