
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Mathematica harjoitustehtäviä liittyen perusaritmetiikkaan.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se Mathematica-pääsivulta löytyvään harjoituspohjaan.
- 1. Strategiapelissä rakennetaan uudelle planeetalle makean veden säiliötä. Säiliö on ympyräpohjainen lieriö, jonka korkeus on 320 metriä ja pohjan säde 1000 metriä. Säiliöstä haihtuu vettä keskimäärin 100 litraa minuutissa. Kuinka monta planeetan vuotta säiliössä riittäisi vettä, ennen kuin täysi säiliö pelkästään haihtumisen vuoksi olisi tyhjentynyt? Planeetan vuosi on 3 ⋅ 107 sekuntia. Vihje: Kertomerkki on joko välilyönti tai *; numeroiden tapauksessa * on selkeämpi (ihmiselle).
- 2. Trooppisen vuoden pituus on 365 vrk 5 h 48 min 45 s ja Maan pyörähdysaika akselin ympäri 23 h 56 min 4 s. Ilmoita murtolukuna, kuinka monta pyörähdystä Maa tekee trooppisessa vuodessa. Mikä tulos on desimaalilukuna? Vihje: Kertomerkki on joko välilyönti tai *; numeroiden tapauksessa * on selkeämpi (ihmiselle).
- 3. Sievennä lauseke
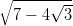 . Laske myös likiarvo 100 desimaalilla.
Vihje: Kokeile funktioita Simplify ja FullSimplify. Neliöjuurifunktio on Sqrt; symboli löytyy
myös paletista. Likiarvon laskeminen: N.
. Laske myös likiarvo 100 desimaalilla.
Vihje: Kokeile funktioita Simplify ja FullSimplify. Neliöjuurifunktio on Sqrt; symboli löytyy
myös paletista. Likiarvon laskeminen: N.
- 4. Laske summat ∑ k=1nk2, kun n = 2, 3, 4, 5, 6, 7, 8, 9, 10. Jaa tulokset tekijöihin. Ovatko jotkin summat jaottomia, so. alkutekijöitä? Vihje: Tarvittavia funktioita: Sum, FactorInteger, PrimeQ. Taulukoita voi tehdä funktiolla Table. Liittämällä loppuun määre //TableForm taulukko saadaan tulostetuksi havainnollisempaan muotoon.
- 5. Tutki, millaisia tarkkoja arvoja saadaan lausekkeelle sin(π∕n), kun n on luonnollinen luku. Mitä tarkoittaa, että osa tuloksista on (ainakin näennäisesti) kompleksilukuja? Missä tapauksissa tulos ei sisällä imaginaariyksikköä? Vihje: Tarvittava funktio on FunctionExpand. Muista iso alkukirjain ja hakasulut: Sin[Pi/n].
- 6. Laadi taulukko sini- ja kosinifunktioiden arvoista välillä 0∘ – 90∘ yhden asteen välein. Vihje: Taulukoita voi tehdä funktiolla Table. Liittämällä loppuun määre //TableForm taulukko saadaan tulostetuksi havainnollisempaan muotoon. Trigonometristen funktioiden argumenttien tulee olla radiaaneissa. Luku π kirjoitetaan Pi; se voidaan myös valita paletista. Muista iso alkukirjain ja hakasulut: Sin[Pi/4], Cos[0]. Katso dokumentaatiosta: Degree.
- 7. Lukua π approksimoidaan luvulla
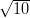 . Laske absoluuttinen virhe ja suhteellinen virhe
prosenteissa.
Vihje: Luku π on Pi ja
. Laske absoluuttinen virhe ja suhteellinen virhe
prosenteissa.
Vihje: Luku π on Pi ja 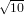 ilmaistaan Sqrt[10]. Molemmissa tapauksissa voidaan symbolit valita
myös paletista.
ilmaistaan Sqrt[10]. Molemmissa tapauksissa voidaan symbolit valita
myös paletista.
- 8. Stirlingin kaavan mukaan on
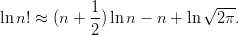
Approksimointi on sitä tarkempi, mitä suurempi n on. Laske absoluuttinen ja suhteellinen approksimaatiovirhe, kun n = 10, 100, 1000. Vihje: Muodosta lausekkeet absoluuttiselle ja suhteelliselle virheelle n:n funktiona ja sijoita näihin tarvittavat n:n arvot korvaussääntöä käyttäen.
- 9. Laske lausekkeen (1 +
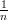 )n likiarvo yhä isommilla arvoilla n ja tutki, miten tämä
lähestyy Neperin lukua e.
Vihje: Likiarvot halutulla tarkkuudella saadaan funktiolla N. Neperin luku on E; se voidaan
valita myös paletista, jolloin symboli näyttää hieman erikoiselta pikku e:ltä. Aloita
varovaisesti; älä syötä kovin suuria lukuja n. Tulokset voi kerätä taulukoksi Table-funktiolla.
)n likiarvo yhä isommilla arvoilla n ja tutki, miten tämä
lähestyy Neperin lukua e.
Vihje: Likiarvot halutulla tarkkuudella saadaan funktiolla N. Neperin luku on E; se voidaan
valita myös paletista, jolloin symboli näyttää hieman erikoiselta pikku e:ltä. Aloita
varovaisesti; älä syötä kovin suuria lukuja n. Tulokset voi kerätä taulukoksi Table-funktiolla.
- 10. Laske summan ∑ k=0n(−1)k∕k! likiarvo yhä isommilla arvoilla n ja tutki, miten summan käänteisarvo lähestyy Neperin lukua e. Vihje: Tarvittavia funktioita: Sum, N. Neperin luku on E; se voidaan valita myös paletista, jolloin symboli näyttää hieman erikoiselta pikku e:ltä. Kertoma ilmaistaan yksinkertaisesti huutomerkillä. Tulokset voi kerätä taulukoksi Table-funktiolla.
- 11. Kahden paikkakunnan välinen lyhin etäisyys maapallon pintaa pitkin mitattuna voidaan laskea kaavasta
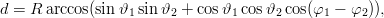
missä 𝜗1 ja φ1 tarkoittavat ensimmäisen, 𝜗2 ja φ2 vastaavasti toisen paikan leveys- ja pituusatetta. R = 6370 km on maapallon säde. Muodosta funktio, jolla voidaan laskea kahden paikkakunnan etäisyys antamalla argumenteiksi paikkojen koordinaatit. Laske a) Helsingin ja Tokion, b) Reykjavikin ja Sydneyn välinen etäisyys, kun paikkakuntien koordinaatit ovat seuraavat:
Vihje: Muodosta funktio siten, että argumentit annetaan asteissa. Arkuskosini on ArcCos. Aste on Degree; katso tarkemmat tiedot dokumentaatiosta.leveyspituusHelsinki 60° 08’ N 25° 00’ E Tokio 35° 40’ N 139° 45’ E Reykjavik 64° 09’ N 21° 58’ W Sydney 33° 55’ S 151° 10’ E
