
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Kompleksilukuihin ja kompleksianalyysiin liittyviä Maple-tehtäviä.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mplK001.tex
Maple-ohjeita muutamaan seuraavaan tehtäväänplot, seq, map, subs, with(plots), complexplot, plot3dseuraavassa xploty tarkoittaa mitä tahansa piirtofunktiota.
with(plots): # Ladataan lisägrafiikkakirjasto
kuva1:=xploty(...): # Kuvan tallettaminen muuttujaan.
kuva2:=xploty(...): # ... ja toinen.
display(kuva1,kuva2); # Näin yhdistetään grafiikkoja.
F:=2*x+exp(x*y); # Lausekkeen arvo muuttuu, kun x ja y muuttuvat.
# MUTTA: F(x,y) tai F(a,b) on vailla mieltä!
# Jos halutaan laskea F:n arvo, kun x=a, y=b, komennetaan:
subs(x=a,y=b,F);
f:=(x,y)-> 2*x+exp(x*y); # Funktiomääritys.
f(a,b) # toimii nyt.Lisää tähän omia ohjeitasi/poista tarpeettomia!
Avainsanat: Maple-ohjeita, mapleohjeet.
- 2. mplK002.tex
Lausu De Moivre’n kaavaa hyödyntäen cos 3φ ,cos 4φ ja sin 5φ cos φ:n ja sin φ:n avulla.Vihje: Sopii käsinlaskuksi, mutta voidaan hyödyntää myös Maplea.
Avainsanat: Kompleksiluvut, De Moivre’n kaava, trigonometriset yhtälöt.
- 3. mplK003.tex
Käsinlasku
Kompleksiluvulla eiα kertominen suorittaa kierron kulman α verran. Tämähän on vanha C1-tuttu olio, tason ℝ2 lineaarikuvaus, jolla niin ollen on matriisiesitys. Johda kiertokuvauksen matriisiesitys muodostamalla tulo w = eiαz, z = x + iy = reiΘPieni (”vapaaehtoinen”) jatko-osa:
Tästä on helppo yleistää mielivaltaisella kompleksiluvulla Reiα kertomiseen. Miten kuvausta voi sanoin kuvailla ?
Avainsanat: Kompleksiluvut, tason kiertokuvaus.
- 4. mplK004.tex
Ykkösen n:nsien juurien käsittelyä varten määrittele Maple-funktiow:=(k,n)->exp(I*2*k*Pi/n);
Piirrä yksikköympyrä ja kaikki
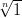 :t joillakin n:n arvoilla.
:t joillakin n:n arvoilla.
Laadi sitten Maple-skripti, jolla voidaan laskea ja piirtää syötteenä annetun mielivaltaisen kompleksiluvun kaikki n:nnet juuret.
> z:=2+3*I : n:=10: % Muuteltava syöterivi
> juuret:=seq(w(k,n),k=0..n-1);
> ? complexplotHuomaa, että eiΘ, Θ ∈ [0, 2π) “piirtää” yksikköympyrän. complexplot on juuri reaalimuuttujan kompleksiplotti.
Kts. tarkemmin
http://www.math.hut.fi/teaching/v/2/02/H/complex6.html
Tässä pikatietoisku kompleksiluvuista:
http://www.math.hut.fi/opetus/Mattie/MattieO/Luentomatskua/
kompleksianalyysi/kompluvut.htmlAvainsanat: Kompleksiluvut, ykkösen juuret, complexplot
- 5. mplK002.tex
Lausu De Moivre’n kaavaa hyödyntäen cos 3φ ,cos 4φ ja sin 5φ cos φ:n ja sin φ:n avulla.Vihje: Sopii käsinlaskuksi, mutta voidaan hyödyntää myös Maplea.
Avainsanat: Kompleksiluvut, De Moivre’n kaava, trigonometriset yhtälöt.
