Luentoja Matemaattiset ohjelmistot-kurssilla 12-28.3.2012
Contents
Matriisin osat ja kokoaminen
clear format compact A=reshape(1:6,2,3),B=ones(2,2),C=diag(1:3) [A B] % Vierekkain [A;C] % Allekkain
A =
1 3 5
2 4 6
B =
1 1
1 1
C =
1 0 0
0 2 0
0 0 3
ans =
1 3 5 1 1
2 4 6 1 1
ans =
1 3 5
2 4 6
1 0 0
0 2 0
0 0 3
Vektorin indeksointi
Laita ensi tilassa <a name> tuonne!!
clear format compact v = [13 5 9 i] v(2) % 2. alkio -> 5 v([1 3 end]) % alkiot 1 3 end -> 13 9 i v(1:3) % alkiot 1 2 3 -> 13 5 9 v(1:3)=-[1 2 3] % Vektorin osan muuttaminen v([1 1 end-1 2 1]) % Saa toistaa ja järjestää. v([1 3])=NaN % Skalaarin laajennussääntö v % NaN -2.0000 NaN i
v =
Columns 1 through 3
13.0000 5.0000 9.0000
Column 4
0 + 1.0000i
ans =
5
ans =
13.0000 9.0000 0 + 1.0000i
ans =
13 5 9
v =
Columns 1 through 3
-1.0000 -2.0000 -3.0000
Column 4
0 + 1.0000i
ans =
-1 -1 -3 -2 -1
v =
Columns 1 through 3
NaN -2.0000 NaN
Column 4
0 + 1.0000i
v =
Columns 1 through 3
NaN -2.0000 NaN
Column 4
0 + 1.0000i
Matriisin indeksointi
clear format compact A=[14 33;9 8] A(1,1) % --> 3 A(1,2) % --> 33 %{ Voidaan indeksoida myös yhdellä indeksillä. Silloin ajatellaan matriisi pitkänä, sarakkeittain jonoutettuna vektorina. %} A(3) % <--> A(2,1) [A(3) A(1,2)]
A =
14 33
9 8
ans =
14
ans =
33
ans =
33
ans =
33 33
Lisää matriisin indeksoinnista
A = magic(6) B = A(3,5) C = A([1,2,3],4) % Sarakkeen 4 alkiot riveiltä 1 2 3 D = A(4,[1,1,1]) % [A(4,1) A(4,1) A(4,1)] E = A([2,5],[3,1]) % Rivien 2 5 sarakkeet 3 1 F = A(:,4) % Koko 4. sarake G = A(4,:) % Koko 4. rivi H = A(:); % A jonoutettuna sarakkeittain size(H) % Pitkä pystyvektori H' % Näytetään transponoituna. A(1:3,[2 3 end-1])=NaN % Päivitys vastaavasti kuin vekt. % Matriisi A siis muuttuu.
A =
35 1 6 26 19 24
3 32 7 21 23 25
31 9 2 22 27 20
8 28 33 17 10 15
30 5 34 12 14 16
4 36 29 13 18 11
B =
27
C =
26
21
22
D =
8 8 8
E =
7 3
34 30
F =
26
21
22
17
12
13
G =
8 28 33 17 10 15
ans =
36 1
ans =
Columns 1 through 11
35 3 31 8 30 4 1 32 9 28 5
Columns 12 through 22
36 6 7 2 33 34 29 26 21 22 17
Columns 23 through 33
12 13 19 23 27 10 14 18 24 25 20
Columns 34 through 36
15 16 11
A =
35 NaN NaN 26 NaN 24
3 NaN NaN 21 NaN 25
31 NaN NaN 22 NaN 20
8 28 33 17 10 15
30 5 34 12 14 16
4 36 29 13 18 11
Esimerkki: Rivioperaatiot Gaussin eliminoinnissa
Etsi:(CTR-F Gauss). Ehdotus: Kopioi komentorivejä omaan editoriisi ja käy ajatuksella läpi vaiheita ainakin johonkin saakka. Tee omia muistiinpanoja.
Looginen indeksointi
%{ Hyvin tehokas tapa data-alkioiden valitsemiseen perustuu bittikuvioilla "bitpatterns" indeksointiin. %} % <html> % <a href="http://math.tkk.fi/~apiola/matlab/opas/lyhyt/perusteet.html"> % Lyhyt opas, CTR-F: loogisten </a> % </html> clear vk=[1 3 4 2 5 6 2 1 6 7 4 5 3 2 1 2 3]; % Varmuuskertoimet vk >= 3 % Tuloksena looginen vektori, jossa 1 vastaa ehdon toteutumista. vk(vk>=3) % Indeksoidaan loogisella vektorilla.
ans =
Columns 1 through 11
0 1 1 0 1 1 0 0 1 1 1
Columns 12 through 17
1 1 0 0 0 1
ans =
3 4 5 6 6 7 4 5 3 3
Looginen valinta matriisille
%{ Toimii aivan samoin kuin vektorille. Voidaan valita loogisten operaattoreiden, kuten < > <= >= == ~ tai loogisten is-funktioiden, kuten isprime, isfinite, ... avulla. %} % Esim: clear A=magic(6) A>30 % Bittimatriisi A(A>30) % Ehdon toteuttavat alkiot (pystyvektorina)
A =
35 1 6 26 19 24
3 32 7 21 23 25
31 9 2 22 27 20
8 28 33 17 10 15
30 5 34 12 14 16
4 36 29 13 18 11
ans =
1 0 0 0 0 0
0 1 0 0 0 0
1 0 0 0 0 0
0 0 1 0 0 0
0 0 1 0 0 0
0 1 0 0 0 0
ans =
35
31
32
36
33
34
Luentotehtävä:
% Poimi kaikki A:n alkiot, jotka ovat alkulukuja ja > 10. % Sijoita vastaaville kohdille A:han arvo Inf. % Tiedoksi: Looginen "and" on & % % % I = (isprime(A) & (A > 10)) A(I) A(I)=Inf
I =
0 0 0 0 1 0
0 0 0 0 1 0
1 0 0 0 0 0
0 0 0 1 0 0
0 0 0 0 0 0
0 0 1 1 0 1
ans =
31
29
17
13
19
23
11
A =
35 1 6 26 Inf 24
3 32 7 21 Inf 25
Inf 9 2 22 27 20
8 28 33 Inf 10 15
30 5 34 12 14 16
4 36 Inf Inf 18 Inf
Luentotehtävä: (vrt. Lyhyt opas)
%{ Muodostetaan yksikkövälillä (0,1) tasaisesti jakautuneista satunnaismuuttujista koostuva 10 x 10 matriisi. Voidaan kysyä vaikka seuraavia: Kuinka moni alkio on vähintään 0.2 ? Mikä on kaikkien näiden summa? Kuinka moni on välillä (0.4,0.6) ? %}
Grafiikka, perusasiat
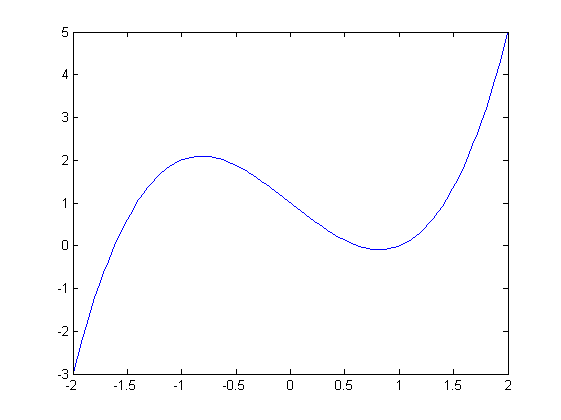
% * plot - 2d-datapisteiden piirto, tasokäyrät % * fplot, ezplot - Funktion piirto, adaptiivinen pisteiden valinta % * plot3 - avaruuskäyrät, periaate aivan sama kuin plot:lla % * mesh,surf,surfc,surfl ... Pinta avaruudessa % * contour - Korkeuskäyräpiirros (myös ezcontour) % % Esim: % % Piirrä
![$$ \ \ \ \ \ y=x^3-2 x +1, x\in [-2,2]$$](Luentoja1_eq74299.png)
x=linspace(-2,2,100); % 100 on oletus.
y=x.^3 -2*x +1;
plot(x,y)